Таќырыбы: ІІ-ретті сызықтарды канондық түрге келтіру. ІІ-ретті сызық инварианттары. Центрлік және центрлік емес сызықтарды классификациялау.
Алдыңғы vі-тарауда эллипс, гипербола және параболаны олардың жабайы теңдеулері арқылы жеке-жеке қарастырдық. Енді осы үш қисықтың координаталар системасында қалай орналасатынын зерттейік. Ғылым мен техникада бұл екінші ретті қисықтың жалпы теориясынын ерекше маңызы зор.
Жоғарыда аталған үш қисықтың жалпы теңдеуін зерттегенде оның теориясымен тығыз байланысып жатқан түзу сызықтар да кездеседі. Сон- дықтан жалпы бір теңдеуді қарастырғанда, онда бірнеше геометриялық бейнелердің қасиеттері кездеседі. Бұл тарауда бір тік бұрышты координаталар системасынан екінші тік бұрышты координата системасына көшкенде екінші ретті сызықтардың жалпы теңдеуінің қалайша түр-ленетінін және оның жабайы түрге келу әдістерін зерттеп, керекті формулаларды қорытып шығарамыз.
§1.Екінші ретті сызықтардың жалпы теңдеуі. Екінші ретті сызықтардың жалпы теңдеуі мынадай түрде жазылады:
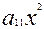 +
+ 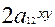 +
+ 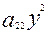 +
+ 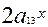 +
+ 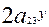 +
+ 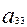 =0, (1)
=0, (1)
мұндағы 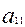 ,
, 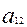 ,
, 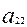 ,
, 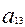 ,
, 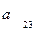 - теңдеудің коэффиценттері,
- теңдеудің коэффиценттері, 
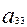 - бос мүше, 11,12,23,22,13,33- коэффиценттердің индекстері. Екінші ретті сызықтардың жалпы теңдеуі алты мүшеден, яғни екінші дәрежелі үш мүшеден, бірінші дәрежелі екі мүшеден және бос мүшеден құралған.
- бос мүше, 11,12,23,22,13,33- коэффиценттердің индекстері. Екінші ретті сызықтардың жалпы теңдеуі алты мүшеден, яғни екінші дәрежелі үш мүшеден, бірінші дәрежелі екі мүшеден және бос мүшеден құралған.
Мұндай жалпы теңдеу қандай жағдайда эллипс, гипербола немесе парабола болады? Ол коэффиценттердің мәндеріне байланысты. Мәселен,
1). Егер 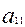 =
= 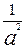 ,
, 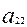 =
= 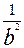 ,
, 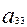 =-1,
=-1, 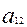 =
= 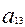 =
= 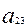 =0 болса, онда
=0 болса, онда 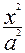 +
+ 
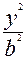 =1 - эллипс:
=1 - эллипс:
2). Егер 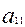 =
= 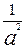 ,
, 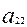 =-
=- 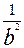 ,
, 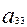 =-1,
=-1, 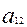 =
= 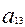 =
= 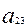 =0 болса, онда екінші ретті сызық
=0 болса, онда екінші ретті сызық 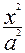 -
- 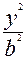 =0 – гипербола:
=0 – гипербола:
3). Егер 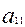 =
= 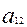 =
= 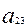 =
= 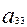 =0,
=0, 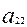 =1,
=1, 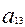 =-p болса, онда екінші ретті сызық
=-p болса, онда екінші ретті сызық 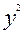 =-2рх – парабола болады.
=-2рх – парабола болады.
Коэффиценттердің кейбір мәндерінде екінші ретті сызық басқа геометриялық бейнелерге де ауысуы мүмкін. Мысалы,
1). Егер 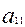 =1,
=1, 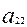 =-1,
=-1, 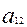 =
= 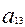 =
= 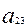 =
= 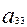 =0 болса, онда
=0 болса, онда 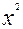 -
- 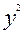 =0, (х+у)(х-у)=0, х+у=0, x-y=0 - екі түзудің теңдеуі:
=0, (х+у)(х-у)=0, х+у=0, x-y=0 - екі түзудің теңдеуі:
2). Егер 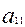 =
= 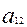 =
= 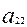 =0,
=0, 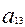 =4,
=4, 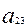 =2,
=2, 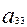 =5 болса, онда 8х+4у+5=0 бір түзуі шығады.
=5 болса, онда 8х+4у+5=0 бір түзуі шығады.
Сонымен, (1) теңдеу коэффиценттерінің мәндеріне байланысты эллипсті, гиперболаны, параболаны немесе басқа геометриялық бейнені (мысалы, түзуді) көрсетуі мүмкін. Сондықтан бұл теңдеудің координаталар системасындағы геометриялық мағынасын зерттеу үшін оның коэффиценттеріне байланысты қандай болатындығын тексеру керек. Бір тік бұрышты координаталар системасына көшкенде теңдеудің коэффиценттері өзгеріледі. Ал әрбір теңдеу сызықтың координаталар системасында қалай орналасатындығын анықтаумен қатар, оның координаталар системасына тәуелсіз ішкі қасиетін анықтауы да мүмкін. Ендеше, кез-келген тік бұрышты координаталар системасында мәндері өзгерілмей отыратын коэффиценттердің функциялары болуы керек. Ал бір тік бұрышты координаталар системасынан екінші тік бұрышты координаталар системасына көшкенде мәндері сақталатын коэффиценттердің функцияларын инварианттар деп атайды. Басқаша айтқанда, бір системадан екінші системаға көшкенде (1) жалпы теңдеудің коэффиценттерінің мәндері өзгерілмесе (немесе кейбір коэффиценттерінң қосындысы не көбейтіндісі сақталса), ондабұл коэффиценттер инварианттар деп аталады. Сондықтан келесі параграфтарда теңдеудің түрленуін тексерумен қатар, осы инварианттарды да іздеуге кірісеміз. Инвариант деген сөз өзгермейді (сақталады) деген мағына береді.
§ 2. Координаталардың бас нүктесін көшіру және екінші ретті сызықтардың жалпы теңдеуін түрлендіру. Теңдеулердің инварианттары. Ескі координаталар системасы хОу, жаңа координаталар системасы Х 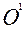 У болсын. Жаңа координаталар системасы мен ескі координаталар системасы бағыттас, ал оның бас нүктесінің координаталары
У болсын. Жаңа координаталар системасы мен ескі координаталар системасы бағыттас, ал оның бас нүктесінің координаталары 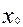 ,
, 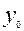 болсын, яғни
болсын, яғни 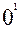 (
(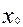 ,
, 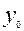 ). Сонда координаталар системасын түрлендірудің бірінші формуласы бойынша:
). Сонда координаталар системасын түрлендірудің бірінші формуласы бойынша:
х=X+ 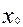

y=Y+ 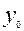
Енді осы х пен у мәндерін (1) теңдеуге қойып түрлендірейік;
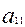 (Х+
(Х+ 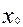 )
) 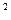 +2
+2 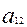 (Х+
(Х+ 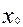 )(У+
)(У+ 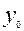 )+
)+ 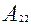 (У+
(У+ 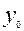 )
)  +2
+2 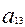 (Х+
(Х+ 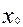 )+
)+
+2 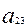 (У+
(У+ 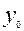 )+
)+ 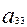 =0,
=0,
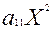 +2
+2 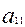 Х
Х 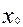 +
+ 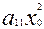 +2
+2 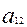 ХУ+2
ХУ+2 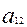 Х
Х 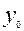 +2
+2 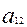 У
У 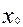 +2
+2 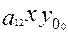 +
+
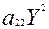 +2
+2 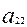 У
У 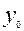 +
+ 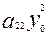 +2
+2 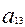 Х+2
Х+2 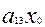 +2
+2 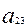 У+2
У+2 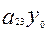 +
+ 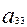 =0,
=0,
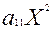 +2
+2 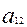 ХУ+
ХУ+ 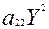 +2(
+2(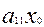 +
+ 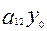 +
+ 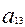 )Х+2(
)Х+2(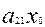 +
+ 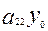 +
+
+ 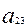 )У+
)У+ 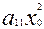 +2
+2 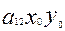 +
+ 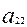
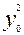 +2
+2 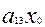 +2
+2 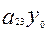 +
+ 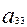 =0 (2).
=0 (2).
Жаңа координаталар системасында шығарылған (2) теңдеуді (1) теңдеумен салыстырсақ, мынадай қасиеттер байқалады:
1). Екінші дәрежелі мүшелерінің коэффиценттері өзгерілген жоқ;
2). Бірінші дәрежелі мүшелерінің коэффиценттері жоғарғы (1) жалпы теңдеудің дербес туындылары болды, өйткені х пен у-тің орнына  (
(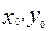 ) нүктесінің координаталары қойылған;
) нүктесінің координаталары қойылған;
3). Бос мүшелері (1) теңдеудің барлық мүшелеріндей алты мүшеден құрылған; мұнда ескі система координаталарының орына жаңа системаның бас нүктесінің координаталары (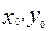 ) қойылады.
) қойылады.
Егер (1) жалпы теңдеудің сол жағын 2Ғ(х, у) немесе қысқаша 2Ғ деп белгілесек, онда ол 2Ғ(х, у)=0 не 2Ғ=0 түрінде жазылады.
(1) теңдеудің дербес туындылары:
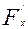 (x, y)=
(x, y)= 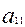 x+
x+ 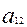 y+
y+ 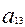 ,
, 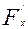 =
= 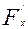 (x, y),
(x, y),
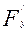 (x, y)=
(x, y)= 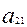 x+
x+ 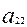 y+
y+ 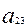 ,
, 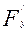 =
= 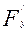 (x, y).
(x, y).
х пен у-тің орнына 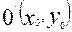 координаталарын қойсақ
координаталарын қойсақ
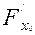 =
= 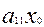 +
+ 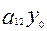 +
+ 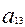 , (A)
, (A)
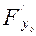 =
= 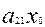 +
+ 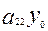 +
+ 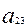 .
.
Енді (2) теңдеу былай жазылады:
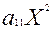 +2
+2 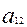 ХУ+
ХУ+ 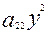 +2
+2 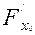 Х+2
Х+2 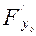 У+2
У+2 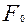 =0 (3)
=0 (3)
мұндағы 2 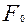 =
= 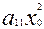 +2
+2 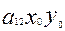 +
+ 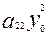 +2
+2 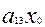 +2
+2 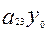 +
+ 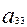 ,
,
өйткені 2 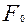 (
(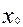 ,
, 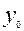 )=2
)=2 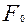 деп белгілейік.
деп белгілейік.
Сөйтіп, осьтердің бағыттарын өзгертпей координаталардың бас нүктесін кез-келген бір нүктеге көшірсек, онда жаңа координаталар системасындағы екінші ретті сызықтың жалпы түрленген теңдеуі мынадай болады.
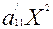 +2
+2 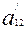 ХУ+
ХУ+ 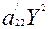 +2
+2 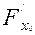 Х+2
Х+2 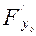 У+2
У+2 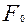 =0, (
=0, (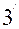 )
)
мұндағы 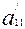 =
= 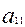 ,
, 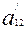 =
= 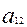 ,
, 
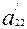 =
= 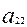 .
.
Осы (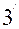 ) теңдеуді немесе (3) теңдеуді (1) теңдеумен салыстырсақ,
) теңдеуді немесе (3) теңдеуді (1) теңдеумен салыстырсақ, 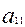 ,
, 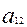 ,
, 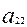 коэффиценттері мәндерінің өзгермегенін көреміз. Ендеше, олар инварианттар болады. Сондықтан олар былайша белгілейік.
коэффиценттері мәндерінің өзгермегенін көреміз. Ендеше, олар инварианттар болады. Сондықтан олар былайша белгілейік.
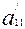 =
= 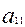 =
= 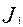 -бірінші инвариант,
-бірінші инвариант,
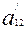 =
= 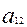 =
= 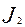 - екінші инвариант.
- екінші инвариант.
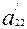 =
= 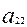 =
= 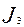 - үшінші инвариант.
- үшінші инвариант.
(3)немесе (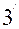 ) теңдеуінің екінші дәрежелі мүшелерінде
) теңдеуінің екінші дәрежелі мүшелерінде 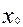 және
және 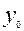 жоқ, яғни
жоқ, яғни 
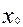 ,
, 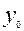 координаталарына бұл теңдеудің екінші дәрежелі үш мүшесі тәуелді емес. Енді осы (
координаталарына бұл теңдеудің екінші дәрежелі үш мүшесі тәуелді емес. Енді осы (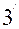 ) теңдеуді былайша жазуға болады:
) теңдеуді былайша жазуға болады:
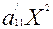 +2
+2 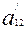 ХУ+
ХУ+ 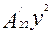 +2
+2 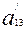 Х+2
Х+2 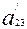 +
+ 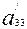 =0, (
=0, (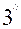 )
)
Осы (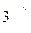 ) теңдеумен (3) теңдеуді салыстыврып,. Олардың сәйкес коэффиценттерін ің өз ара байланысмтарын жазайы
) теңдеумен (3) теңдеуді салыстыврып,. Олардың сәйкес коэффиценттерін ің өз ара байланысмтарын жазайы


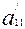 =
= 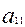 ,
, 
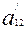 =
= 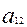 ,
, 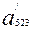 =
= 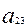 (
(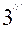 )
)
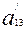 =
= 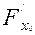 ,
, 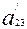 =
= 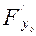 ,
, 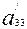 =2
=2 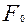 .
.
(1) теңдеудің коэффиценттерінен құрылатын үшінші ретті анықтауышты жазайық:
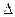 =
= 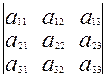 (4) Осы сияқты (
(4) Осы сияқты (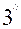 ) теңдеудің үшінші ретті анықтауышы:
) теңдеудің үшінші ретті анықтауышы:

 =
= 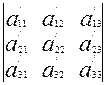 (5)
(5)
Ал (5) анықтауышқа ( ) теңдіктердегі жаңа коэффиценттердің мәндерін қояйық:
) теңдіктердегі жаңа коэффиценттердің мәндерін қояйық:

 =
= 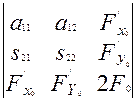 (
(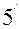 )
)
Енді жалпы біртектес екінші дәрежелі теңдеуді алайық. Біртектес теңдеу деп барлық мүшелеріндегі белгісіздердің дәрежелері бірдей болатын теңдеуді айтамыз. Екінші ретті сызықтың жалпы біртектес екінші дәрежелі теңдеуі мынадай түрде жазылады:
2Ғ(х, у,z) = 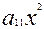 +2
+2 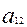 xy+
xy+ 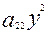 +2
+2 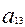 xz+2
xz+2 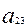 yz+
yz+ 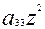 =0 (
=0 (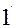 )
)
Осыдан дербес туындыларды табайық:
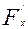 =
= 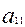 x+
x+ 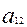 y+
y+  z,
z,
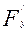 =
= 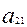 x+
x+ 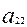 y+
y+ 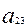 z, (B)
z, (B)
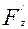 =
= 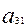 x+
x+ 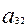 y+
y+ 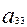 z.
z.
Осы үш (в) теңдіктің екі жағын сәйкес х,у,z-ке көбейтіп қоссақ, мынау шығады
х 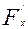 +y
+y 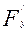 +z
+z 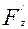 =2F,
=2F,
немесе
x 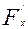 +y
+y 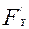 +z
+z 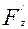 =2F(x,y,z) (
=2F(x,y,z) (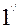 )
)
Осы (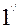 ) теңдеу Эйлер формуласы деп аталады. Мұны жоғарғы жазылған (
) теңдеу Эйлер формуласы деп аталады. Мұны жоғарғы жазылған (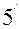 ) анықтауышты түрлендіргенде қолданамыз. Анықтауыштың қасиеттерін пайдаланып, (
) анықтауышты түрлендіргенде қолданамыз. Анықтауыштың қасиеттерін пайдаланып, (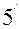 ) теңдікті түрлендірейік. Ол үшін бірінші тік жолмен екінші тік жолды сәйкес
) теңдікті түрлендірейік. Ол үшін бірінші тік жолмен екінші тік жолды сәйкес 
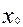 мен
мен 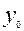 -ге көбейтіп, үшінші тік жолды алсақ, онда (
-ге көбейтіп, үшінші тік жолды алсақ, онда ( ) анықтауыш мынадай болады:
) анықтауыш мынадай болады:
 =
= 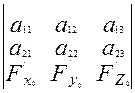 (
( )
)
Енді дербес туындылардың (А) мәндері мен Эйлер формуласы (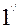 ) бойынша:
) бойынша:
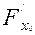 -
- 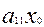 -
- 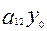 =
= 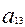
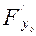 -
- 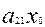 -
- 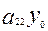 =
= 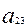
 2
2 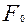 -
- 
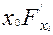 -
- 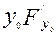 =
= 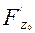
Мұнда 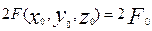 деп қысқаша белгілейік,
деп қысқаша белгілейік, 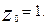 Ал
Ал 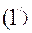 форму-ладағы х,у,z ағымдық координаталардың орнына
форму-ладағы х,у,z ағымдық координаталардың орнына 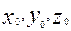 координаталары қойылған.
координаталары қойылған.
(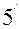 ) анықтауыштың түрленуі сияқты (
) анықтауыштың түрленуі сияқты (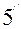 ) анықтауыштағы бірінші екінші жатық жолдарды сәйкес
) анықтауыштағы бірінші екінші жатық жолдарды сәйкес 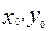 -ге көбейтіп, үшінші жатық жолдан алсақ, онда тағы да дербес туындылардың теңдеулері мен Эйлер формуласы бойынша мынадай анықтауыш шығады:
-ге көбейтіп, үшінші жатық жолдан алсақ, онда тағы да дербес туындылардың теңдеулері мен Эйлер формуласы бойынша мынадай анықтауыш шығады:
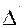 =
= 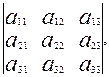 (
( )
)
Бұдан мынадай қортынды шығады: (1) теңдеудің үшінші ретті анықтауышы ( ) теңдеудің үшінші ретті анықтауышына тең болады:
) теңдеудің үшінші ретті анықтауышына тең болады: 
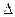 =
= 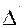 `(6)
`(6)
Бұл теңдік төртінші инвариантты көрсетеді. Оны былайша белгілейміз:
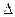 =
= 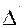 =
= 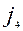
Соныменг, ең ақырында мынадай қортындыға келеміз. Осьтердің бағыттарын өзгертпей координаталардың бас нүктесін еркімізше бір нүктеге көшірсек, онда жаңа координаталар системасы ның түрленуіне сәйкес төрт инвариант шығады:
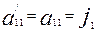
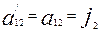
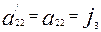 (
(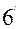 )
)
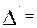
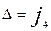
Инварианттарды 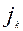 әрпімен белгіледік, мұндағы
әрпімен белгіледік, мұндағы  k=1,2,3,4. Енді инварианттарды ескі координаталар системасының коэффиценттері арқылы жазайық:
k=1,2,3,4. Енді инварианттарды ескі координаталар системасының коэффиценттері арқылы жазайық:
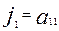
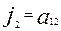
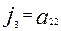 (7)
(7)
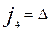
Ескерту. Екінші ретті сызықтың жалпы біртектес теңдеуі жоғарыда мынадай түрде жазылады:
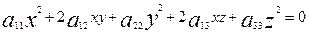 (
(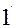 )
)
Бұл біртектес екінші дәрежелі теңдеу алты мүшеден құрылған, ал үш х, у, zайнымалы шамалар коэффиценттерінің қасында мынадай екінші дәрежелі болып жазылған: 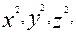 уz, xz, xy. Барлық мүшелерінің дәрежелері бірдей болғандықтан, бұл (
уz, xz, xy. Барлық мүшелерінің дәрежелері бірдей болғандықтан, бұл (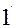 ) теңдеуі біртектес теңдеу деп аталады.
) теңдеуі біртектес теңдеу деп аталады.
Егер z=1 болса, онда (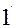 ) теңдеуінің дербес жағдайы бізге белгілі екінші ретті сызықтың жалпы теңдеуі болады, яғни
) теңдеуінің дербес жағдайы бізге белгілі екінші ретті сызықтың жалпы теңдеуі болады, яғни
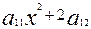 ху+
ху+ 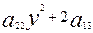 х+2
х+2 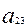 у+
у+ 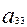 =0 (1)
=0 (1)
Бұл теңдеу екінші ретті қисықтың біртектес емес теңдеуі деп аталады.
Егер аффиндік координаталар системасына сәйкес келетін М(х, у) нүктесінің координаталарының орнына 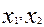 z-ті енгізсек, яғни х пен у-ті былайша өрнектесек:
z-ті енгізсек, яғни х пен у-ті былайша өрнектесек:
x= 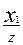 , y=
, y= 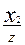
онда осы теңдіктерді қанағаттандыратын 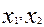 z сандары М нүктесінің біртектес координаталары деп, ал егер z=1 болса, онда х, у біртектес емес координаталар деп аталады.
z сандары М нүктесінің біртектес координаталары деп, ал егер z=1 болса, онда х, у біртектес емес координаталар деп аталады.
Осы анықтамаға сәйкес (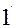 ) теңдеуінің х, у, z координаталары біртектес, ал (1) теңдеуінің х, у координаталары біртектес емес.
) теңдеуінің х, у, z координаталары біртектес, ал (1) теңдеуінің х, у координаталары біртектес емес.
1- мысал. Берілген 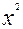 +2ху+4
+2ху+4 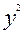 +2х+4=0 теңдеуіндегі координаталар системасының бас нүктесі
+2х+4=0 теңдеуіндегі координаталар системасының бас нүктесі 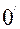 (1, 1) нүктесіне көшірілген, ал координаталар бағыттары өзгерілмеген. Екінші ретті сызықтың жаңа координаталар системасындағы теңдеуін табайық.
(1, 1) нүктесіне көшірілген, ал координаталар бағыттары өзгерілмеген. Екінші ретті сызықтың жаңа координаталар системасындағы теңдеуін табайық.
Шешуі. Жаңа координаталар системасында екінші ретті сызықтың теңдеуі жалпы түрде (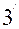 ) формуласы бойынша жазылады:
) формуласы бойынша жазылады:
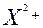 2ХУ+4
2ХУ+4 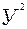 +2
+2 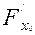 Х+2
Х+2 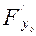 У+2
У+2 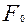 =0.
=0.
Берілген теңдеуді 2F деп белгілеп, дербес туындыларды табайық:
 2
2 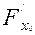 =2
=2 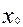 +2
+2 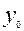 +2,
+2, 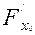 =
= 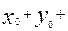 1=1+1+1=3,
1=1+1+1=3,
 2
2 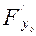 =2
=2 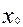 +8
+8 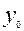 ,
, 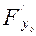 =
= 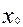 +4
+4 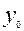 =1+4=5.
=1+4=5.
Бос мүше
2 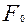 =
= 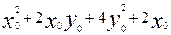 =1+2+4+2+4=13
=1+2+4+2+4=13
Іздеген теңдеу: 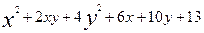 =0
=0
2-мысал. Екінші ретті сызықтың 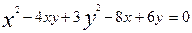 теңдеуі берілген. Ал координаталар осьтерінің бағыттары сақталып, оның бас нүктесі жаңа нүктеге көшірілген. Жаңа координаталар системасында түрленген теңдеудің
теңдеуі берілген. Ал координаталар осьтерінің бағыттары сақталып, оның бас нүктесі жаңа нүктеге көшірілген. Жаңа координаталар системасында түрленген теңдеудің 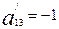 ,
, 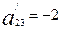 коэффиценттері берілген. Жаңа координаталар системасындағы теңдеудің бос мүшесін және оның ескі системаға сәйкес келетін бас нүктесінің координаталарын табайық.
коэффиценттері берілген. Жаңа координаталар системасындағы теңдеудің бос мүшесін және оның ескі системаға сәйкес келетін бас нүктесінің координаталарын табайық.
Шешуі. Берілген теңдеудің үшінші ретті анықтауышын табайық.
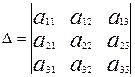 =
= 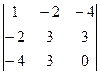 =0+24+24-48-9=-9
=0+24+24-48-9=-9
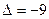
Жаңа координаталар системасындағы теңдеуді былайша жазайық:

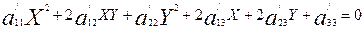 .
.
Төртінші инвариантты қолданайық: 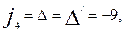 сонда
сонда
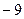 =
= 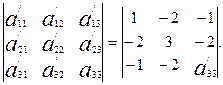
Осыдан бос мүшені табайық:
-9= 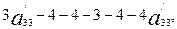
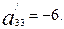
Сонымен, жаңа координаталар системасындағы екінші ретті сызықтың теңдеуі мынадай болады:
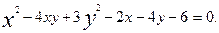
Енді жаңа координаталар системасының бас нүктесінің координаталарын табу үшін, берілген теңдеудің дербес туындыларды тауып, онан шыққан теңдеулер системасын шешейік. Берілген теңдеуді 2F деп белгілейік. Сонда
2Ғ= 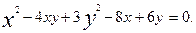
Осыдан дербес туындыларды табайық:
2 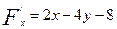 ,
,
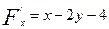 ,
,
2 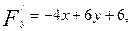
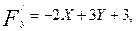
Ал 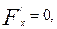
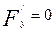 . Сонда
. Сонда
х-2у-4=0,
-2x+3y+3=0
Осы теңдеулер системасынан центрдің координаталарын табамыз:
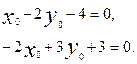
Осыдан 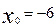 ,
, 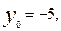 ал бас нүкте
ал бас нүкте 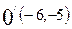 болады.
болады.
Егер екінші ретті сызықтың центрі координаталардың бас нүктесінде жатса, онда осыған сәйкес дербес туындылар нольге тең болуы керек: 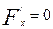 ,
, 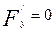 . Бұл туралы келесі параграфта толық ұғым береді.
. Бұл туралы келесі параграфта толық ұғым береді.
§ 3. Екінші ретті сызықтың центрі. Екінші ретті центрлік сызықтың теңдеуі. Анықтама. Екінші ретті сызықтың центрі деп содан жүргізілген барлық хордалар қақ бөлетін нүктені айтамыз. 
Бұл анықтама бойынша екінші ретті сызық өз центріне симметриялы болады. Координаталардың бас нүктесі екінші ретті сызықтың центрінде жатса, онда осы центрден өтетін кез-келген хорданың екі ұшындағы 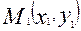 ,
, 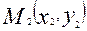 нүктелерінің координаталары өз ара ең болады, яғни
нүктелерінің координаталары өз ара ең болады, яғни 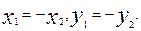
 және
және  нүктелері екінші ретті сызықтың бойында жатқандықтан, олардың -
нүктелері екінші ретті сызықтың бойында жатқандықтан, олардың - 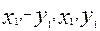 координаталары сызықтың теңдеуін қанағаттандырады. Ендеше, мұндай теңдеу екінші дәрежелі болады. Сондықтан координаталардың бас нүктесін екінші ретті сызықтың центріне көшірсек, онда бұл сызықтың теңдеуінде бірінші дәрежелі мүшелер болмау керек. Сөйтіп, координаталардың бас нүктесі екінші ретті сызықтың центрі болуы үшін оған қажетті және жеткілікті тшарт: екінші ретті сызықтың теңдеуінде (х пен у енетін) бірінші дәрежелі мүшелер жоқ болу керек. Алдыңғы 2-параграфта осьтердің бағыттарын өзгертпей, координаталардың бас нүктесін
координаталары сызықтың теңдеуін қанағаттандырады. Ендеше, мұндай теңдеу екінші дәрежелі болады. Сондықтан координаталардың бас нүктесін екінші ретті сызықтың центріне көшірсек, онда бұл сызықтың теңдеуінде бірінші дәрежелі мүшелер болмау керек. Сөйтіп, координаталардың бас нүктесі екінші ретті сызықтың центрі болуы үшін оған қажетті және жеткілікті тшарт: екінші ретті сызықтың теңдеуінде (х пен у енетін) бірінші дәрежелі мүшелер жоқ болу керек. Алдыңғы 2-параграфта осьтердің бағыттарын өзгертпей, координаталардың бас нүктесін 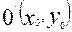 нүктесіне көшірдік. Егер осы нүкте екінші ретті сызықтың центрі болса, онда (3) теңдеуде бірінші дәрежелі мүшелер болмайды. Ендеше (3) теңдеудегі дербес туындылар нольге тең:
нүктесіне көшірдік. Егер осы нүкте екінші ретті сызықтың центрі болса, онда (3) теңдеуде бірінші дәрежелі мүшелер болмайды. Ендеше (3) теңдеудегі дербес туындылар нольге тең:
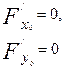 .
.  (8)
(8)
немесе
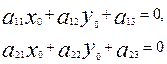 (8)
(8)
Енді екінші ретті сызықтың біртектес емес жалпы теңдеуі берілсін:
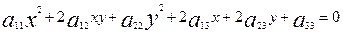 (1)
(1)
Мұнын сол жағын 2Ғ(х,у)=2Ғ деп белгілеп, оның дербес туындыларын жазайық:

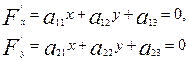 (а)
(а)
2-параграфтағы (2) теңдеуді қысқаша мынадай түрде жазайық:
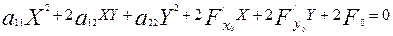 (3)
(3)
Мұнын дербес туындылары:
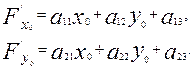 (в)
(в)
(а) –теңдіктердегі Х,У –кез келген нүктенің координаталары, ал (в) –теңдіктердегі 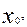
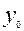 - жаңа системаның бас нүктесінің (ескіге қарағандағы) координаталары. Сонымен, координаталардың бас нүктесі екінші ретті сызықтың центрі болса, онда жоғарғы айтуымыз бойынша дербес туындылар нольге тең:
- жаңа системаның бас нүктесінің (ескіге қарағандағы) координаталары. Сонымен, координаталардың бас нүктесі екінші ретті сызықтың центрі болса, онда жоғарғы айтуымыз бойынша дербес туындылар нольге тең:
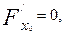
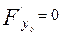 (
(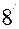 )
)
немесе
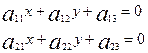 (
(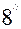 )
)
Ал 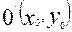 нүктесі – екінші ретті сызықтың центрі. Ендеше (3) теңдеудің бірінші дәрежелі мүшелері болмауға тиіс, яғни (8) шарт орындалады. Сондықтан (3) теңдеуі мынадай түрге келеді:
нүктесі – екінші ретті сызықтың центрі. Ендеше (3) теңдеудің бірінші дәрежелі мүшелері болмауға тиіс, яғни (8) шарт орындалады. Сондықтан (3) теңдеуі мынадай түрге келеді:
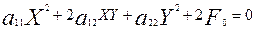 (9)
(9)
Бұл теңдеу екінші ретті центрлік сызықтың теңдеуі деп аталады. Оның центрінің координаталарын табу үшін ( ) теңдеулері системасын шешу керек.
) теңдеулері системасын шешу керек.
( ) теңдеулерінің әрқайсысы бір түзуді кескіндейді, ендеше екі түзудің қиылысқан нүктесі екінші ретті сызықтың центрі болады. Бұл теңдеулер системасын шешкенде үш түрлі жағдайдың кездесуі мүмкін.
) теңдеулерінің әрқайсысы бір түзуді кескіндейді, ендеше екі түзудің қиылысқан нүктесі екінші ретті сызықтың центрі болады. Бұл теңдеулер системасын шешкенде үш түрлі жағдайдың кездесуі мүмкін.
1- жағдай. Екі түзу ( ) бір нүктеде қиылысса, онда
) бір нүктеде қиылысса, онда
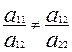 немесе
немесе 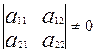 (А). Бұл жағдай екінші ретті сызық центрлік сызық деп аталады.
(А). Бұл жағдай екінші ретті сызық центрлік сызық деп аталады.
2- жағдай. Екі түзу ( ) өз ара параллель болса, онда
) өз ара параллель болса, онда
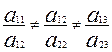 немесе
немесе 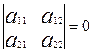 (В)
(В)
3- жағдай. Екі түзу (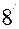 ) беттессе, онда екі түзу бір теңдеуге айналады, яғни мына шарт орындалады:
) беттессе, онда екі түзу бір теңдеуге айналады, яғни мына шарт орындалады:
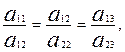 (Г)
(Г)
Осы жағдайда екінші ретті сызықтың центрі анықталмайды,яғни оның центрі осы беттескен түзулердің бойында болады. Мұндай түзу центрлер сызығы деп аталады.
Енді жоғарғы үш жағдайды былай айтуға болады.
1). Егер 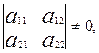 онда (
онда (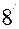 ) теңдеулерінің жалғыз шешімі болады. Сондықтан екінші ретті сызықтың (1) бір ғана центрі бар.
) теңдеулерінің жалғыз шешімі болады. Сондықтан екінші ретті сызықтың (1) бір ғана центрі бар.
2). Егер (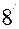 ) теңдеулері бірігіп шешілмесе, онда екінші ретті сызықтың (1) центрі болмайды.
) теңдеулері бірігіп шешілмесе, онда екінші ретті сызықтың (1) центрі болмайды.
3). Егер (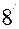 ) теңдеулерінің шешімдері анықталмаса, онда екінші ретті сызықтың (1) центрлері көп болады, яғни екінші ретті сызықтың центрлері бір түзудің бойында жатады.
) теңдеулерінің шешімдері анықталмаса, онда екінші ретті сызықтың (1) центрлері көп болады, яғни екінші ретті сызықтың центрлері бір түзудің бойында жатады.
1-мысал. Екінші ретті сызықтың 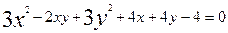 теңдеуі берілген. Оның центрін табайық.
теңдеуі берілген. Оның центрін табайық.
Шешуі. (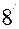 ) теңдеулер системасы бойынша іздеген центрдің координаталарын табайық:
) теңдеулер системасы бойынша іздеген центрдің координаталарын табайық:
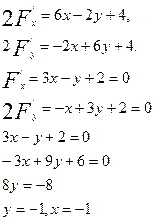
Сонда екінші ретті сызықтың центрі М(-1, -1) болады. Сонымен, екінші ретті сызық – не эллипс, не гипербола, небір нүктеден қиылысатын екі түзу.
2-мысал. 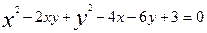 теңдеуімен берілген екінші сызықтың шешімі бар ма
теңдеуімен берілген екінші сызықтың шешімі бар ма
Шешуі. Алдыңғы мысал сияқты берілген теңдеуден дербес туындыларды табамыз:
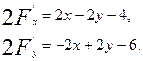
Мұны қысқартқаннан кейін мынадай теңдеулер шығады:
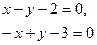
Бұл теңдеулер х пен у-тің мәндері табылмайды, яғни екі теңдеу бірігіп шешілмейді. Сондықтан берілген екінші ретті сызықтың центрі жоқ, яғни екінші ретті сызықтың центрі шексізде болады.
3-мысал. Берілген теңдеудің дербес туындылары:
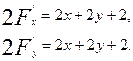
Осыдан 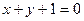 . Демек, берілген қисықтың центрлері
. Демек, берілген қисықтың центрлері 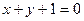 түзуінің бойында болады, яғни екінші ретті сызыққа центр болатын нүктелер өте көп, олардың бәрі де осы
түзуінің бойында болады, яғни екінші ретті сызыққа центр болатын нүктелер өте көп, олардың бәрі де осы 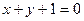 түзуінің бойында жатады. Мұндай түзуді екінші ретті сызықтың центрлерінің түзуі дейміз.
түзуінің бойында жатады. Мұндай түзуді екінші ретті сызықтың центрлерінің түзуі дейміз.
§ 4. Екінші ретті центрлік сызықтың теңдеуін түрлендіру. 3-параграфта координаталардың бас нүктесін центрге көшіргенде екінші ретті центрлік сызықтың теңдеуі мынадай болған еді:
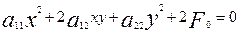 (9). Енді осытеңдеуді бұдан да гөрі ыңғайлы түрге келтірейік. Ол үшін мұндағы бос мүшенің толық мәнін жазып, соңы түрлендірейік.
(9). Енді осытеңдеуді бұдан да гөрі ыңғайлы түрге келтірейік. Ол үшін мұндағы бос мүшенің толық мәнін жазып, соңы түрлендірейік.
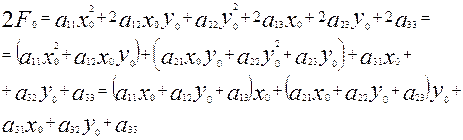
немесе
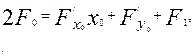
мұндағы 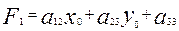
Көшірілген координаталардың бас нүктесі 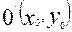 екінші ретті сызықтың центрі болады. Сондықтан:
екінші ретті сызықтың центрі болады. Сондықтан:
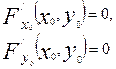 (8)
(8)
немесе
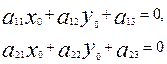 (8)
(8)
Мына (8) шарт орындалғандықтан, енді бос мүше мынадай болады:
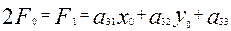 (10)
(10)
(8) теңдеулерден 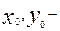 ді табамыз:
ді табамыз:
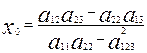 ,
,
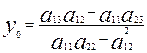 (11)
(11)
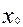 мен
мен 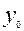 -дің мәндерін (10) теңдеуге қойып, іздеген бос мүшені берілген теңдеудің коэффиценттері арқылы өрнектейік:
-дің мәндерін (10) теңдеуге қойып, іздеген бос мүшені берілген теңдеудің коэффиценттері арқылы өрнектейік:
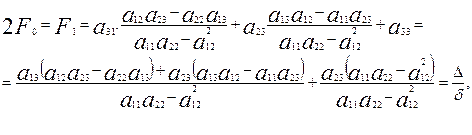

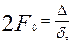 (12)
(12)
мұндағы
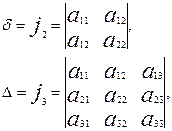 (13)
(13)
Бос мүшенің осы (12) мәнін (9) теңдеуге қойып, ізжеген центрлік сызықтың теңдеуін былайша жазайық:
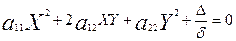 (14)
(14)
Сөйтіп, координаталардың бас нүктесін екінші ретті сызықтың центріне көшірсек, оның теңдеуі жаңа координаталар системасында (14) теңдеудей ыңғайлы түрде шығады. Бұл теңдеуде:
1) бастапқы екінші дәрежелі үш мүшесі өзгермейді, ескі ағымдық координаталардың орнына жаңа ағымдық координаталар қойылады;
2) бос мүше орнына үшінші ретті анықтауыштың екінші ретті анықтауышқа қатынасы алынады. Бұл жағдайда жалпы теңдеу екінші ретті центрлік сызықтың теңдеуі болуы үшін, мына екінші ретті анықтауыш (13) нольге тең болмау керек:
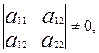
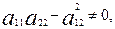 яғни
яғни 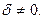
Мысал. Координаталардың бас нүктесі 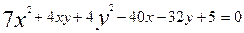 теңдеуімен берілген екінші ретті сызықтың центріне көшірілген. Екінші ретті сызықтың жаңа координаталарсистемасына сәйкес центрлік теңдеуін жазайық.
теңдеуімен берілген екінші ретті сызықтың центріне көшірілген. Екінші ретті сызықтың жаңа координаталарсистемасына сәйкес центрлік теңдеуін жазайық.
Шешуі. Бос мүше мынаған тең:
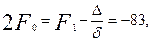
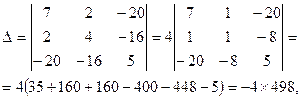
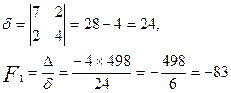
Сонда екінші ретті центрлік сызықтың теңдеуі 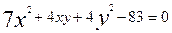 болады.
болады.
§ 5. Екінші ретті центрлік сызықтың теңдеуін жабайы түрге келтіру. Координаталар осьтерінің бағыттарын өзгертпей, оның бас нүктесін екінші ретті сызықтың центріне көшірсек, онда эллипс пен гиперболаның жалпы теңдеуі мынадай түрге келеді.
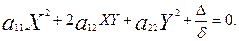 (14)
(14)
Енді осы теңдеуді жабайы түрге келтірейік. Ол үшін координаталар осьтерін екінші ретті сызықтың симметриялы осьтермен беттескенше бір 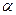 бұрышына бұрайық (қисықтың центрі жаңа координаталар системасының бас нүктесіболады.). Ал координаталар системасын
бұрышына бұрайық (қисықтың центрі жаңа координаталар системасының бас нүктесіболады.). Ал координаталар системасын 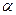 бұрышына бұрғанда мынадай формулалар шыққан:
бұрышына бұрғанда мынадай формулалар шыққан:
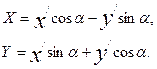
Осы х пен у-тің мәндерін (14) теңдеуге қояйық:
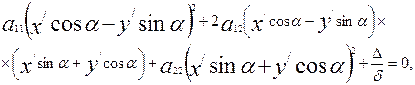
Осы теңдеудегі жақшаны ашып түрлендірсек, жаңа координаталар системасы арқылы мынадай теңдеуді табамы:
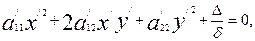 (
(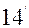 )
)
мұндағы
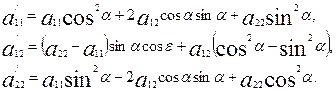 (15)
(15)
Егер (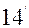 ) теңдеудегі
) теңдеудегі 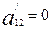 шарт орындалса, яғни
шарт орындалса, яғни 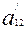 коэффиценті алынған
коэффиценті алынған 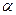 бұрышының кейбір мәнінде нольге тең болса, онда координаталар осьтері қисықтың осьтерімен беттеседі, яғни
бұрышының кейбір мәнінде нольге тең болса, онда координаталар осьтері қисықтың осьтерімен беттеседі, яғни
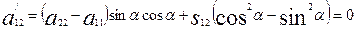
немесе
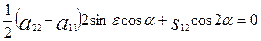
Осыдан түрлендіріп, tg2 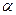 -ны табайық:
-ны табайық:
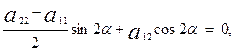
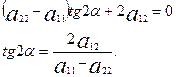 (16)
(16)
Осы формуладан координаталар системасының қандай бұрышқа бұрылғанын білуге болады. Жаңа координаталар системасына сәйкес (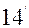 ) теңдеуіне қойылған шарт бойынша екінші мүше жойылатын болғандықтан (
) теңдеуіне қойылған шарт бойынша екінші мүше жойылатын болғандықтан (
 2015-04-12
2015-04-12 5998
5998








