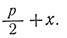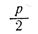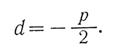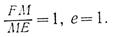Эллипс

Лекция.

Таќырыбы: Эллипстің, гиперболаның және параболаның канондық теңдеуі. Эллипс пен гиперболаның директрисасы. Эллипстің, гиперболаның және параболанның полярлық теңдеуі.

Эллипс.

Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтардың қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын элипис дейді.

Енді элипистің жабайы теңдеуін қорытып шығарайық. Ол үшін анықтамаға сәйкес сызба сызамыз.

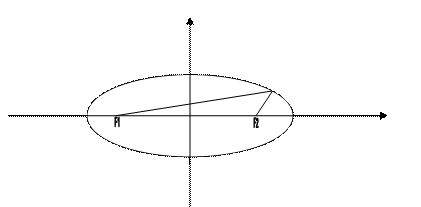
Анықтама бойынша:

.

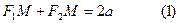Мұндағы 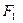және 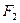-фокус деп аталатын берілген нуктелер, М(х,у)- элипстің бойындағы кез келген нукте, 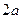-тұрақты шама.

Егер 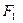және 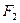нуктелерінің ара қашықтығы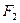 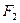=2c десек, онда осы екі нүктенің координаталары былай аныкталады:

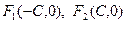
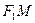және 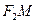қашықтықтарын

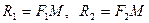
деп белгілесек, онда (1) теңдік мынадай түрде жазылады:

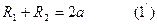
Екі нүтенің ара қашықтығының формуласы бойынша:

Осы мәндерді 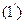теңдікке қояйық:

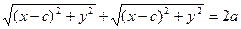
Бұл теңдікті түрлендіріп, элипистің жабайы теңдеуін табайық:

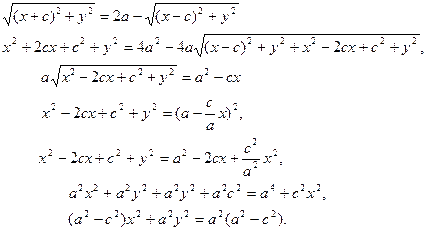
егер болса, 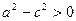болады, сондықтан

деп белгілейік, олай болса 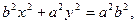осыдан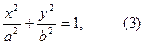

Мұндағы х пен у-элипстің бойындағы кез келген нүтелердің координаталары, а-элипстің үлкен жарты осі, b-оның кіші жарты осі. Бұл теңдеу элипстің жабайы теңдеуі деп аталады. (3) теңдеудің дәрежесі жұп болғандықтан, элипстің бойындағы M нүктесінің координаталары. Әрқашан да мынадай болады: 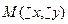. Сондықтан координаталар осьтері элипске семметриялы, ал семметриялы осьтердің қиылысқан нүктесі элипстің центрі болады.

Элипистің түрін оның жабайы теңдеуі бойынша зерттеу

Элипистің жабайы теңдеуін у арқылы шешейік: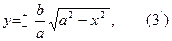

Мұндағы х пен у-айнымалы шамалар. х-тің мәндеріне сәйкес у-тің әртүрлі мәндері шығады. Енді 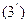теңдеуін зерттейік:

1.Егер х=0 болса, онда 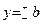, яғни 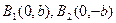болады. Бұлар кордината осінде жатқан элипстің бойындағы нүктелер.

2.Егер 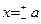болса, онда у=0, яғни 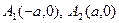болады. Бұлар абсцисса осінде жатқан элипстің бойындағы нүктелер.

3. теңдеуі х-тің барлық нақты мәндерінде қанағаттанады. Егер х-тің шамасы а-дан артық болса, онда у жорамал сан болады. Сондықтан элипстің бойында жатқан нақты нүктелердің координаталары a мен b-нің сәйкес шамаларынан артық болмау керек. Элипстің барлық нүктелері қабырғалары 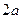және 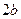болатын тік төртбұрышпен шектелген яғни 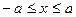және .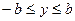

4. 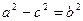теңңдігінен: a>b, a>c немесе 2a>2b, 2a>2c. Мұндағы 2a-элипстің үлкен осіне; 2b-элипстің кіші осі, 2c-элипстің фокустарының ара қашықтығы.

Элипстің жабайы теңдеуін зерттегеннен мынадай қорытынды шығады. Элипс координаталар системасында өзінің центріне симметриялы болып орналасатын тұйық қисық сызық болады. Элипстің центрі координаталар системасының центрінде жатады. 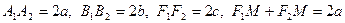немесе .

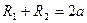Егер 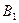мен 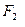нүктелерін қоссақ, онда 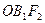тік бұрышты үшбұрыш шығады. Осыдан Пифогор теоремасы бойынша:

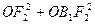, осыдан 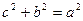. Бұл теңдік a,b,c шамаларының өз ара байланысын көрсетеді. 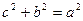теңдігінен 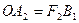екенін көреміз, яғни үлкен жарты ось әрқашан да фокустың нүктесінен ордината осінің бойындағы 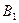немесе 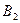нүтесіне дейінгі қашықтыққа тең болады. 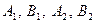нүктелері элипстің төбелері деп аталады.

Радиус-вектор және эксцентриситет.

1-параграфта элипстің жабайы теңдеуін шығарумен байланысты мынадай теңдік шықты:

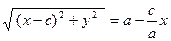. Бұл теңдіктің сол жағы 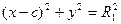, сонда 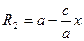. Анықтама бойынша 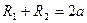. 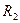-нің мәнін осы анықтамаға қойып, 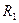-ді табайық: 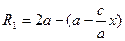, 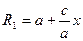. Сонымен, мынадай екі теңдік шықты:

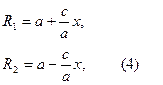
мұндағы 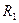және 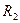элипстің радиус –векторлары деп аталады. (4) теңдік осы элипстің радиус-векторларының формуласы. 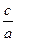қатынасы элипстің эксцентриситеті деп аталады. Эксцентриситет e әрпімен белгіленеді.

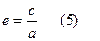
2-параграфтағы 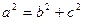формуласынан a>c дегенбіз. Ендеше, элипстің эксцентриситеті әрқашанда дұрыс бөлшек болады, яғни e<1 немесе .

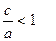Енді (4) теңдіктегі 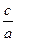қатынасының орнына e–ні қойсақ, мынадай теңдіктер шығады:

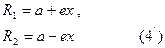
Егер 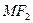абсцисси осіне перпендикуляр болса, онда 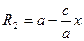формуласындағы x=c болады. 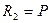деп белгілесек, онда 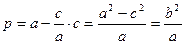яғни 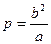, (6) мұндағы p фокальдық параметр деп аталады.

Элипске жүргізілген жанама мен нормальдың теңдеулері.

Элипстің теңдеуі және оның бойында жатқан бір нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін қорытып шығарайық.

1. 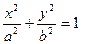теңдеуі, 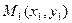, нүктесі берілген. Енді (Ж) жанама мен (N) нормалының теңдеулерін іздейік. 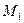нүктесімен қиюшы (Қ) түзуін жүргізейік. Берілген 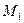нүктесі қозғалмай 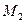нүктесі қозғалатын нүктелер болсын. 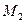нүктесі берілген 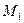нүктесіне ұмтылғанда, қиюшы (Қ) түзуі жанамаға ұмтылады, яғни 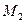нүктесінің координаталары 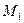нүктесінің координаталарына тең болғанда 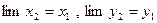, яғни қиюшы түзу жанама болады. Қиюшы түзудің (екі нүктеден өтетін түзудің) теңдеуін жазайық:

.

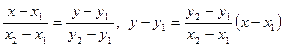Қиюшы түзудің 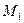және 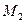нүктелерінің координаталары элипстің теңдеуін қанағаттандырады:

.

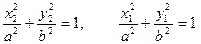Осы екі теңдіктің біріншісінен екіншісін алып тастап, 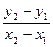қатынасын табайық:

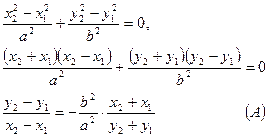
нүктесі нүктесіне беттескенде 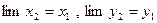болады. Cондықтан, 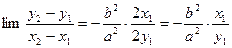. Қиюшы түзудің теңдеуіне (А) қатынасының мәнін табайық:

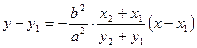
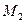нүктесі 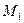нүктесімен беттескенде қиюшы түзу жананма болады. Осыдан жанаманың теңдеуі шығады:

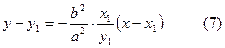
2. Берілген жанамаға перпендикуляр болатын түзудің нормаль деп атайды. -жанамаға перпендикуляр. Ендеше, екі түздің перпендикулярлық шарты 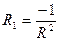бойынша нормальдық теңдеуі жазылады:

.

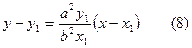Aл,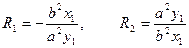

3. Жанама теңдеуін қолайлы түрге келтірейік. Ол үшін (7) теңдеуді түрлендірейік.

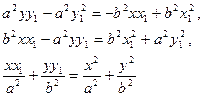
Осы теңдіктің оң жағыдағы қосынды элипстің жабайы формуласы бойынша бірге тең. Сонда іздеген жанаманың жабайы теңдеуі шағады: .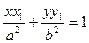

4. Нормальдың теңдеуін екінші түрге келтірейік. Ол үшін (8) теңдеуді түрлендірейік:

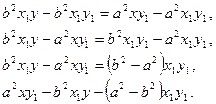
(2) формула бойынша 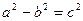, сонда

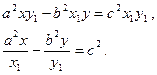
1-мысал.

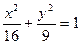элипске нүктесінде жанама және нормаль болатын түзулердің теңдеулерін табайық:

Шешуі: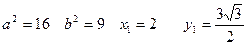

1) Жанаманың теңдеуін (9) формула бойынша табамыз:

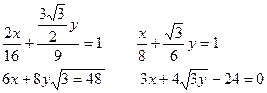
2) Нормальдың теңдеуін (10) формула арқылы табамыз:

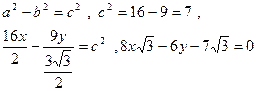
2-мысал.

Берілген 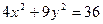элипске жанама және y=2x-6 түзуіне перпендикуляр болатын түзулердің теңдеулерін табайық.

Шешуі: Екі түзудің перпендикуляр шарты бойынша (7) теңдеудегі бұрыштық коэффиценттің таңбасы және шамасы кері пропоционал болады:

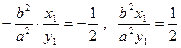
Элипстің теңдеуін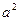ен пен 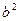-ты тауып, оны алдыңғы теңдікке кояйық:

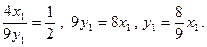
Жанасу нүктесінің координаталары элипстің теңдеуін қанағаттандырады. Сондықтан жанасу нүктесінің координаталарын мына теңдеулерден табайық:

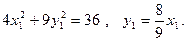
Соңғы теңдеудегі 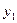мәнін алдыңғысына қойсақ:

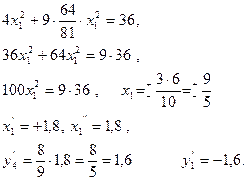
Сонымен, жанасу нүктесі екеу болады: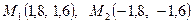

Енді (9) формула бойынша жанаманың теңдеулерін табайық:

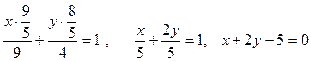
Екінші жанаманың теңдеуі 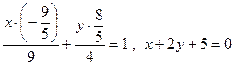. Берілген элипс пен табылған түзулердің графиктері сызбада көрсетіледі.

Нормальдық теңдеуді (8) формула бойынша табайық:

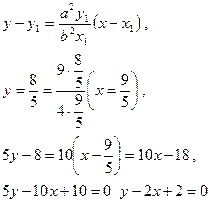
Бұл - нүктесінен өтетін нормаль. Енді 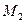нүктесінен өтетін нормальдың теңдеуіне табайық:

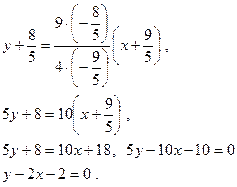
Гиперболаның жабайы теңдеуі

Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырымы әрқашанда тұрақты шама болатын нүктелердің геометриялық орындарын гипербола дейміз

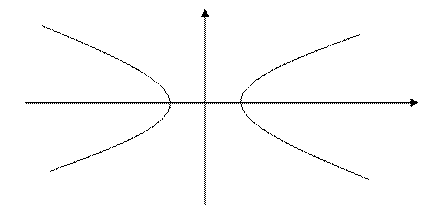
Анықтама бойынша:

2а=F₁M-F₂M

F₁F₂=2C, ОF₂=С болсын (1)

Екі нүктенің ара қашықтығының формуласы бойынша

R ₁= 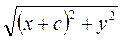R₂ =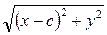

Осы R₁ мен R₂ – нің мәндерін анықтамаға қойып, алгебралық түрлендіру арқылы гиперболаның жабайы теңдеуін табайық

F₁M=R₁ F₂M= R₂

R₁ мен R₂ – нің мәндерін (1) теңдікке қойамыз

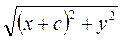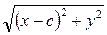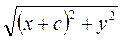- =2a

=2a +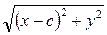

x + 2cx + c² + y² = 4a² 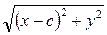+ x² – 2cx + c² + y

cx – a² =a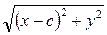

Енді екі жағын а – ға бөлейік:

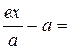
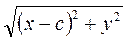
Осы теңдіктің екі жағын квадраттасақ, іздеген теңдеуді табамыз

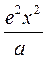-2cx+ a² = x² – 2cx + c² + y²

c² x² – a⁴ = a² x² + a² c² + a² y²

(c² - a²) x² - a² y² = (c² - a²) a²

Егер с² - а² = в² (2)

деп белгілесек, онда в² х² - а² у² = а² в² осыдан

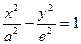(3)

Бұл теңдеу гиперболаның жабайы теңдеуі деп аталады. Мұндағы х,у - гиперболаның

Байындағы кез – келген нүктенің ағымдық координаталары а – гиперболаның нақты жарты осі, b – жорышал жарты ось.

Гиперболаның түрін оның жабайы теңдеуі бойынша зерттеу.

Гиперболаның жабайы теңдеуі у арқы өрнектейік:

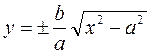
Мұндағы х пен у айнымалы шамалар х – тің мәндеріне сәйкес у – тің мәндері шығады. Осы айнымалы әр түрлі мәндеріне байланысты, гиперболаның координаталар системасында қалай орналасатындығын (3`) теңдеуі арқылы қарастырайық

1) Егер х = +а болса, онда у = 0 болады. Сонда абсцисса осінің бойында гиперболаның екі нүктесі болады. А₁(-а,0), А₂ (а,0)

2) Егер х=0 болса, онда у= ві болады. Мұнда ордината осінің бойында гиперболаның нақты нүктесі жоқ, яғни гипербола ордината осін қиып өтпейді.

3) (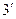) теңдеуіне қарағанда х – тің абсолют мәні өскен сайын у- тің абсолют мәні өсіп отырады.

4) х – тің бір мәнәне у – тің әрқашанда екі мәні сәйкес келеді, яғни аргунттің бір мәніне функцияның екі мәні сәйкес келеді, демек плюс және минус таңбалары у – тің мәндері абсцисса осінің жоғарғы және төменгі жағында жатады.

5) (2) формуладан с>а. с>в. Ал

2с>2а, А₁А₂ =2а, F₁F₂ =2c В₁В₂ =2в

Осы айтылғандарға сүйене отырып, гиперболаның грфигін салуға болады. Сызбадағы А₁ және А₂ - гиперболаның төбелері А₁А₂ - гиперболаның нақты осі, В₁В₂ – жорымал осі. Координаталардың бас нүктесіне қарағанда гипербола симметриялы қисық сызық. х пен у – тің абсалют мәндері өскен сайын гиперболаның екі тармағы өсіп отырады х пен у шексіз болса онда гиперболаның нүктелеріде шексіз болады. Сызбадан ОА₁² + ОВ₁² = А₁В₁ a² + b² =с² А₁ В₁ = ОF₁ = ОF₂ =c

Егер а мен b тең болса, онда 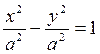немесе x² - y² = a² болады.

Бұл тең қабырғалы гипербола деп аталады. Бұл жағдайдағы фокус координаталары мен осьтердің байланысы мынадай болады

с² - a² = b² а = b сонда с² = 2 a² с = 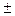а

Радиус – вектор және эксецнтриситет

Осы тараудың 1 – параграфында гиперболаның жабайы теңдеуін дәлелдегенде мынадай теңдік шықты: 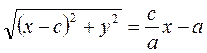Сызбадан F₂M =R₂ =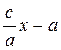

Анықтама бойынша R₁ - R₂ =2а Осыдан R₁- ді табайық:

R₁ =2а + R₂ =2а + 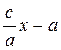R₁ =а +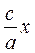

Сонымен R₁ мен R₂ - нің мәндері мынадай болады

R₁ = 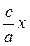+ а R₂ = 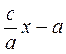(4)

Бұл теңдіктер гиперболаның радиус – векторларының формулалары деп аталады. Гиперболаның екі фокусының ара қашықтығының нақты осіне қатынасы гиперболаның эксецнтриситеті деп аталады. Эксецнтриситет е әріпімен белгіленеді

е = 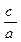(5)

с² – а² =в² Формуласынан с>а, яғни с – тің а – дан артық екенін көреміз. Сонықтан Гиперболаның эксецнтриситеті әрқашанда бірден артық болады е > 1

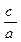( - бұрыс бөлшек)

(4) формулаға е – нің мәнін қойсақ мынау шығады R₁ = ех+а R₂ =ех-а (4^\)

Егер радиу – вектор F₂M =R₂ абцисса осіне перпендикуляр болса онда х =с,

R₁ = 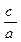с + а, R₂ = 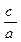с – а, яғни R₁ = 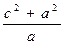R₂ = 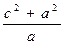болады. (2) теңдікті

қолдансақ, R₂ = 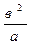, ал R₂ =р деп белгілесек, р = 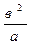(6)

Бұл формула фокальдық радиус – вектордың формуласы деп аталады. R₂=р – фокальдық радиус – вектор.

Гиперболаның асимптоталары.

Анықтама: гиперболаның асимптотасы деп, координатаның бас нүктесінен өтетін және гиперболаның тармақтарымен шексіз алыстағынүктелерге кездестін түзуді айтамыз.

Гиперболаның 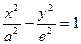теңдеуі және координаталардың бас нүктесінен өтетін түзудің теңдеуі берілген.

Соңғы теңдеудегі игректі бас әріппен белгіледік гиперболаның теңдеуін у арқылы шешіп у = 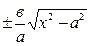оның плюс таңбалы мәнін алайық: у =+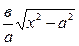

У = 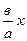теңдеуі мен у = 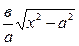теңдеуінің айырымын табайық:

У- у =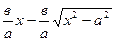

Алдағы мақсат – х шекізге ұмтылғанда (х 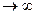) бас әріппен белгіленген. У пен кіші әріппен белгіленгенн у – тің айырымы неге ұмтылатындығын табу.

Басқаша айтқанда, гипербола мен осы түзудің қиылысатын нүктесі бар ма? Қойылған сұраққа жауап беру үшін жоғарғы жазылған теңдіктің оң жағын түйіндес шамаға көбейтіп және оған бөліп түрлендірейік

У- у = 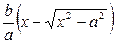= 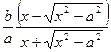У- у = =

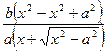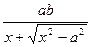
Осыдан

Lіm(У- у) = lіm 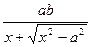Lіm(У- у) = 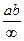=0 Lіm(У- у) =0

Демек, түзу мен гипербола шексізде қиылысады х – тің мәні өскен сайын екі функцияның айырымы нольге ұмтылып, түзу гиперболаның тармағына жақындай береді. Мұндай түзу гиперболаның асимптотасы деп аталады. Гиперболаның асимптотасы әрқашанда екеу болады.

Олардың теңдеулері

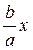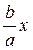y = + y = - (7)

Мұндағы а мен б – гиперболаның жарты осьтері

Бұл екі теңдеуді басқаша жазуға болады

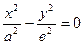
немесе

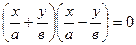яғни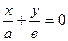

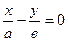
Сызбадан МД = У, М₁Д = у, ОД = х, ММ₁ = МД = М₁Д – М₁Д = У – у, МД Ох

Гиперболаның грфигін құру үшін, оның асимптоталарыныңграфиктерін пайдаланған жөн

1 – мысал. гиперболаның 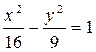теңдеуі берілген. Оның асимптоталарының теңдеуін жазайық

Шешуі: асимптоталардың формуласы (7) бойынша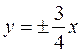

Гиперболаға жүргізілген жанама және нормальдың теңдеулері

Гиперболаның теңдеуі және сол Гиперболаның бойында жатқан нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін табайық

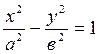теңдеуі мен М₁(х₁, у₁) нүктесі берілген. Енді (ж) жанамасы мен (N) нормальдың теңдеулерін іздейік. Берілген М₁ нүктесінен бір көмекші қиюшы түзу жүргізіп, оның гиперболамен қиылысатын екінші нүктесін М₂(х₂, у₂) деп белгілейік. Гиперболаның бойындағы М₁ мен М₂ нүктелерінің координаталары гиперболаның қанағаттандыратын болғандықтан,

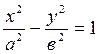
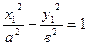
Осы екі теңдеуден 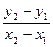қатынасын іздейміз. Ол үшін бірінші теңдеуден екіншісін аламыз, сонда

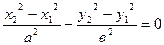
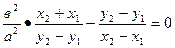
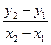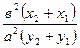= (8)

Ал қиюшы түзудің теңдеуі мынадай болады:

У – у₁= 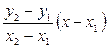(9)

Егер М нүктесін қозғалмайтын, ал М₂ нүктесі М₁ нүктеге ұмтылады деп қарастырайық. (М₁ нүктесі М₂ нүктесінің шегі болсын) М₂ нүктесі М₁ нүктесімен шектескенде, ол қиюшы жанамаға айналады, яғни М₂ нүктесінің координаталары М₁ нүктесінің координаталарына ұмтылады: lіm x₂=x₁ lіm y₂=y₁ Сондықтан (8) теңдіктен

Lіm 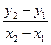= 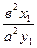(8`)

Ал (9) теңдіктен

У – у₁=lіm ()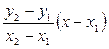

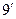(8)теңдігінің мәнін (9*) теңдігіне қойып, іздеген жанаманың теңдеуін табайық:

У – у₁ = 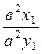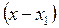(10)

Түзулердің перпендикулярлық шарты бойынша, гиперболаға жүргізілген нормальдың теңдеуі мынадай болады

У – у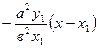₁= (11)

Енді гиперболаға жүргізілген жанама теңдеуінің қолайлы түрін шығарайық. Ол үшін (10) теңдеуіді түрлендірейік

а² уу₁– а² у₁²= б² хх₁ – б² х₁²

б² хх₁ - а² уу₁ = б² х₁² – а² у₁²

Осы теңдіктің екі жағында а² б² бөлсек

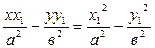
Осыдан гиперболаға жүргізілген жанаманың қолайлы теңдеуі шығады:

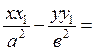1 (10*)

Парабола

Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын нүктелердің геометриялық орындарын парабола дейміз.

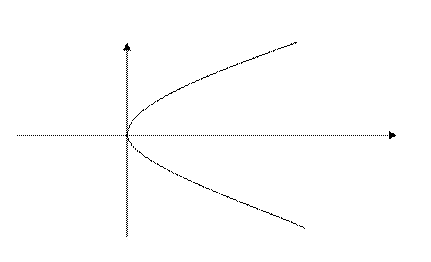
Параболаның жабайы теңдеуін қорытып шығару үшін жоғарғы анықтамаға сәйкес сызба сызайық.

Берілген F нүктесінің координаталары былайша белгіленеді:

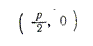
. Бұл нүкте парболаның фокусы деп аталады. Координаталардың бас нүктесінен қашықтықтағы әрі ордината

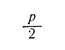
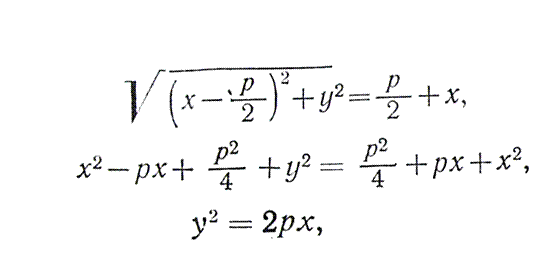
осіне параллель берілген (D) түзуін параболаның директрисасы дейміз. Параболаның бойындағы кез келген нүктені M (x, y) дейік.

Анықтама бойынша:

FM = ME

Екі нүктенің ара қашықтығының формуласы бойынша:

FM =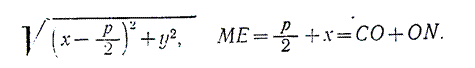

Осы қашықтықтардың мәндерін (1) теңдігіне қойып, параболаның жабайы теңдеуін табамыз:

мұндағы p-берілген фокус пен директрисаныңарасындағы қашықтық, параболаның параметрі; x пен y-параболаның бойындағы кез келген нүктенің ағымдық координаталары.

MF=R параболаның радиус-векторы деп аталады.

Оның ME=FM= +x теңдігінен мынаған тең екенін көреміз:

R=

Параболаның директрисасы 1-сызбадан анықталады:

Параболаның эксцентриситеті:

Параболаның түрін оның жабайы теңдеуі бойынша зерттеу.

Параболаның түрін зерттеу үшін оның жабайы теңдеуін у арқылы шешейік: y =

Осыдан параболаның бойында жататын нүктелерді белгілеп, параболаның координаталар системасында қалай орналасатындығын қарастырайық.

1. Егер х-0, онда у-0. Демек, парабола координаталардың бас нүктесінен өтеді.

2. Егер х-0, онда у-+- 2рх- жорымал сан. Сондықтан ордината осініңң сол жағында параболаның нақты нүктесі болмайды.

3. Егер х –0, онда у-тің осыған сәйкес нақты мәндері болады. Х өскен сайын у-тің абсолют мәні де өсіп отырады. Х-тің әрбір мәніне у-тің әрқашанда екі мәні сәйкес келеді, яғни параболаның абсисса осіне қарағанда симметриялы екі нүктесі болады. Бұл зерттеуден мынадай қорытынды шығады: парабола- координаталардың бас нүктесінен өтіп, абсисса осіне симметриялы, шексізге дейін өсе беретін қисық сызық

Параболаға жүргізілген жанама мен нормальдің теңдеулері.

Параболаның теңдеуі және оның бойында жатқан нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдің теңдеулерін табайық.

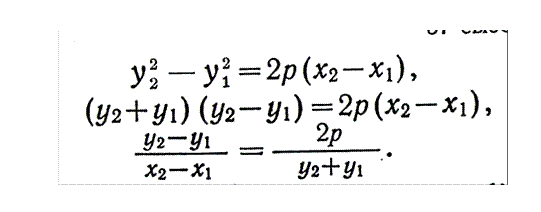
Параболаның диаметрлері. Анықтама. Берілген бағытқа параллель хордалардың ортасындағы нүктелердің геометриялық орындарын параболаның осы бағытқа түйіндес диаметрі дейміз.

Параболаның у2=2рх теңдеуі және осы параболаны қиып өтетін А1В1 хордасының у-ях+і теңдеуі берілген.

А1В1 хордасының А1 және В1 нүктелері параболаның бойында жатқандықтан, бұл екі теңдеуден осы нүктелердің координаталарын табамыз:

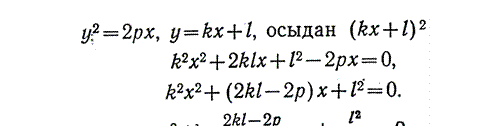
Осы квадрат теңдеуден Виет теоремасы бойынша:

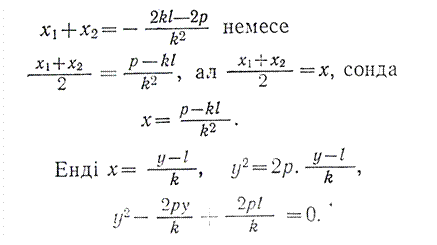
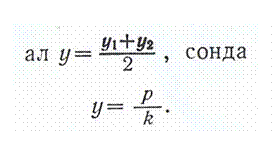
Сонымен, хорданың ортасындағы нүктесінің координаталары:

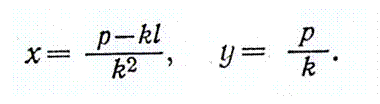
А₁В₁ хордасының ортасындағы С нүктесінің координаталары

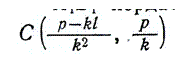
болады. Әрбір параллель хорданың i бос мүшесі әр түрлі болғандықтан, х-тің мәні әрбір хорданың ортасындағы нүкте үшін, мысалы С₁С₂ нүктелері үшін әр түрлі болады.

Ал у=р- хорданың ортасындағы нүктенің ординатасы параболаның параметрі мен хорданың теңдеуінің бұрыштық коэффициентіне тәуелді. Ендеше бұл ордината – барлық параллель хордалардың ортасындағы нүктелер үшін тұрақты шама. Сондықтан берілген я бағытына сәйкес параболаның диаметрі мынадай болады

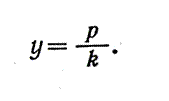
Бұл теңдеуден мынадай қорытындыға келеміз. Параболаның диаметрі абсцисса осіне параллель болады. Демек, параболаның барлық диаметрлері абсцисса осіне параллель болуы керек. Я коэффициентінің мәніне сәйкес абсцисса осіне параллель әр түрлі диаметрлер болуы мүмкін. Егер я-1 болса, онда диаметр у-р болады. Егер я-оо, онда диаметр у-0 болады. Соңғы жағдайда абсцисса осі параболаның диаметрі болады. Бұл параболаның бас диаметрі деп аталады (у-0).

Эллипстің немесе гиперболаның барлық диаметрлері берілген нүктеде қиылысады. Осы диаметрлердің қиылысқан нүктесі эллипстің немесе гипболаның центрі болады. Осыған байланысты эллипс пен гиперболаны центрлік қисықтар дейміз. Ал диаметрлері өз ара параллель болғандықтан, параболаны центрсіз қисық дейміз. Басқаша айтқанда, параллель диаметрлер шексізде қиылысады, сондықтан параболаның центірі шексізде болады