Таќырыбы: ІІ-ретті беттер. Эллипсоид және параболоидтар.Екінші ретті конус. Параболоидтар. Екінші ретті цилиндр.
Дөңгелек цилиндрдің бағыттаушысы- хОу жазықтығындағы радиусы R-ге тең шеңбер, ал жасаушылары апликата осіне параллель (163-сызба) болады. Осы сияқты хОу жазықтығындағы эллипстік
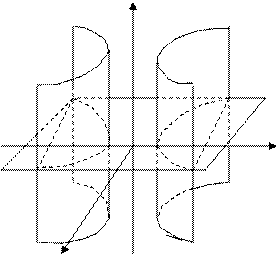
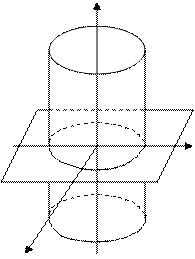
163- сызба 164-сызба
 цилиндрдің бағыттаушысы – эллипс, ал жасаушылары – апликата осіне параллель түзулер. Қалған екі цилиндрлер туралы да осы сияқты айтуға болады (164, 165-сызбалар).
цилиндрдің бағыттаушысы – эллипс, ал жасаушылары – апликата осіне параллель түзулер. Қалған екі цилиндрлер туралы да осы сияқты айтуға болады (164, 165-сызбалар).
Цилиндрлер дегеніміз –шеңбер, эллипс, гипербола, парабола нүктелерінен
солардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер. Бұл шеңбер, эллипс, гипербола және парабола цилиндрлердің бағыттаушылары деп аталады, ал цилиндрлердің беттерінде жатқан түзулер олардың жасаушылары деп аталады.
Егер 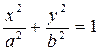 эллипстік цилиндрдегі
эллипстік цилиндрдегі 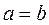 болса, онда айналмалы екінші ретті бет шығады:
болса, онда айналмалы екінші ретті бет шығады: 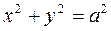 немесе
немесе 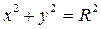 - дөңгелек цилиндр. Сонымен дөңгелек цилиндрді эллипстік цилиндрдің дербес жағдайы деуге болады.
- дөңгелек цилиндр. Сонымен дөңгелек цилиндрді эллипстік цилиндрдің дербес жағдайы деуге болады.
Сөйтіп апликата осіне параллель цилиндрлік беттің теңдеуі мынадай түрде белгіленеді:

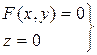 (11)
(11)
Жоғарғы төрт теңдеуді жалпы түрде осылай жазуға болады. хОу жазықтығында (11) теңдеу қисық сызықты көрсетеді, кеңістікте осы қисық сызықтардан өтетін цилиндрлік беттерді кескіндейді.
1-мысал. Кеңістіктегі түзудің параболалық цилиндрмен қиылысатын нүктелерін табайық:

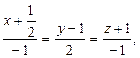 .
. 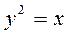 .
.
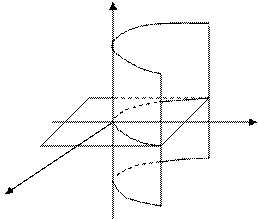
Шешуі. Түзу мен параболалық
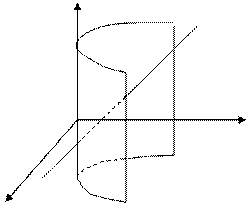
цилиндрдің қиылысатын нүкте лерін табу үшін берілген теңдеулерден x, y, z-тің мәндерін табайық (166-сызба).
-
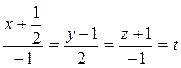 ,
,
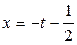 ,
, 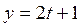 ,
, 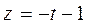 ;
;
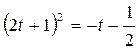 ,
, 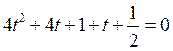
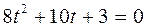 .
.

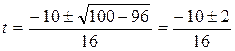 ,
,
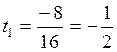 ,
, 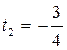 .
.
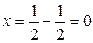 ,
, 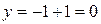 ,
,
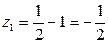 ,
, 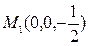 ;
;
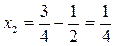 ,
, 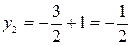 ,
,
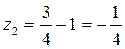 ,
, 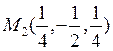 .
.
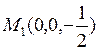 нүктесі апликата осінде (166-сызба), ал
нүктесі апликата осінде (166-сызба), ал 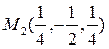 нүктесі цилиндрдің бізге көрінбейтін бетінде жатыр.
нүктесі цилиндрдің бізге көрінбейтін бетінде жатыр.
2-мысал. Мына 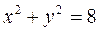 дөңгелек цилиндр мен
дөңгелек цилиндр мен 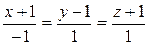 түзуінің қиылысқан нүктелерін табайық.
түзуінің қиылысқан нүктелерін табайық.
Шешуі. Алдыңғы мысалдағыдай мұнда да x, y, z-тің мәндерін табайық.
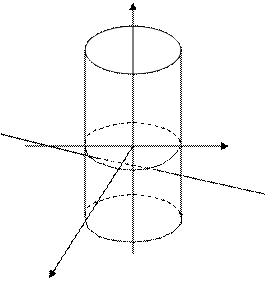
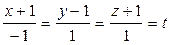 ,
,
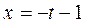 ,
,
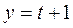 ,
,
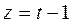 .
.
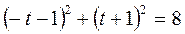 ,
,
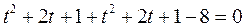 ,
,
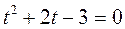 ,
, 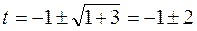 ,
,
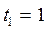 ,
, 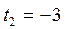 ;
; 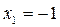 ,
, 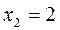 ,
,
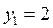 ,
, 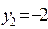 ,
, 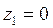 ,
, 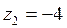 ;
;
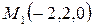 ,
, 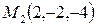 .
.
3-мысал. Мына 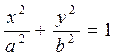 цилиндрінің бетінде жатқанын жүргізейік.
цилиндрінің бетінде жатқанын жүргізейік.
Шешуі. 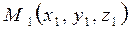 нүктесінен цилиндрге жанама жүргізу үшін мына
нүктесінен цилиндрге жанама жүргізу үшін мына 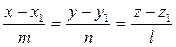 түзуі мен цилиндрдің теңдеуін біріктіріп шығарайық:
түзуі мен цилиндрдің теңдеуін біріктіріп шығарайық:
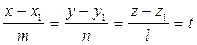 ,
,
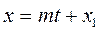 ,
,
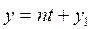 ,
,
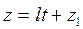 ,
,
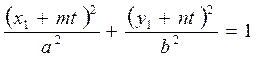
немесе
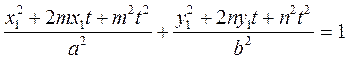 ,
,
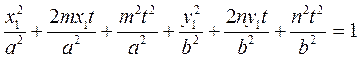 .
.
Осыдан
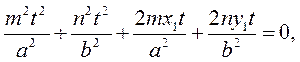
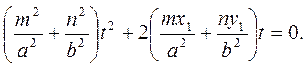
Егер түзу цилиндрді 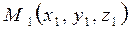 нүктесінен жанаса, онда жоғарғы квадрат теңдеудің түбірлері бірдей болу керек. Ол үшін
нүктесінен жанаса, онда жоғарғы квадрат теңдеудің түбірлері бірдей болу керек. Ол үшін 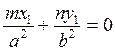 болу керек. Енді жанаманың теңдеуін табайық:
болу керек. Енді жанаманың теңдеуін табайық:
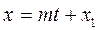 ,
, 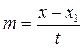 ,
,
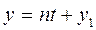 ,
, 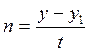 .
.
Енді m мен n-нің мәнін цилиндрлік жанама болу шартының теңдеуіне қояйық:
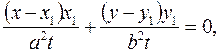
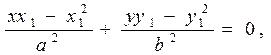
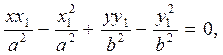
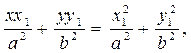
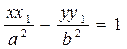 .
.
Конус. Екінші ретті конус деп, берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалғанынан шыққан геометриялық бейнені айтамыз. Конустың бағыттаушысы 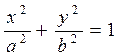 эллипс болсын. Конусты хОу жазықтығына параллель қиып өтетін жазықтық z=c болсын. Конустың жасаушы түзуі координаталардың бас нүктесінен өтсін, яғни конустың төбесі координаталардың бас нүктесінде жатсын. Осы конустың теңдеуін іздейік.
эллипс болсын. Конусты хОу жазықтығына параллель қиып өтетін жазықтық z=c болсын. Конустың жасаушы түзуі координаталардың бас нүктесінен өтсін, яғни конустың төбесі координаталардың бас нүктесінде жатсын. Осы конустың теңдеуін іздейік.
Координаталардың бас нүктесінен және бағыттаушы 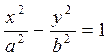 эллипстің (x, y, z) нүктесінен өтетін жасаушы түзудің теңдеуі
эллипстің (x, y, z) нүктесінен өтетін жасаушы түзудің теңдеуі 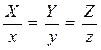 болады, мұнда X, Y, Z – түзудің бойында жатқан кез-келген нүктенің ағымдық координаталары, ал x, y, z – эллипстің
болады, мұнда X, Y, Z – түзудің бойында жатқан кез-келген нүктенің ағымдық координаталары, ал x, y, z – эллипстің
бойындағы нүктенің координаталары. Бізге z=c түзуі берілген. Осы z-тің орнына оның мәнін қояйық:
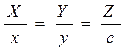 .
.
Осыдан
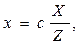
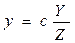 .
.
Осы x пен y-тің мәндерін бағыттаушы эллипстің 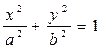 теңдеуіне қойып, іздеген конустың теңдеуін табайық:
теңдеуіне қойып, іздеген конустың теңдеуін табайық:
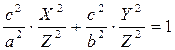 ,
, 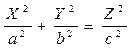 ,
,
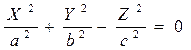 . (12)
. (12)
Бұл конустың перпендикулярлық қимасы эллипс. Егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:
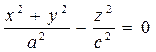 . (12')
. (12')
Бұл – z осінің жанымен қозғалатын
айналмалы конус деп аталады. Егер
a=b=c болса, онда мынадай конус
шығады:
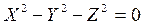 . (12")
. (12")
Сөйтіп, (12) теңдеу төбесі коор-
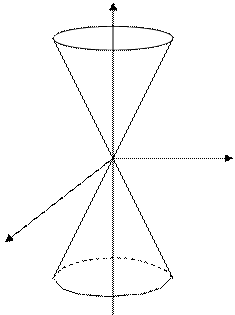 динаталардың бас нүктесінде бола-
динаталардың бас нүктесінде бола-
тын апликата осіне симметриялы
түсетін екінші ретті конустық бетті
кескіндейді (168-сызба).
Қалған екі оське симметриялы
Конустық беттің теңдеулері мынадай
болады:
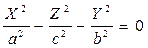 ,
,
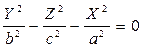 .
.
Бұл теңдеулердің дербес жағдайлары:
a=c, 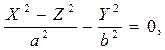
b=c, 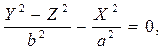
a=b=c, 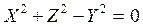 ,
, 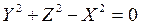 .
.
Геометриялық беттердің кескіні айнымалы x, y, z мәндерінің қандай әріптермен белгіленгендігіне байланысты болмайды. Сондықтан (12") формуласын кіші x, y, z әріптерімен белгілеуге болады. Сонымен, конустық беттің 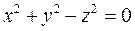 теңдеуін зерттейік. x, y, z – айнымалы шамалар z – ке әртүрлі мән беріп, бұл теңдеудің осы z – тің мәндеріне сәйкес геометриялық мағынасын қарастырайық.
теңдеуін зерттейік. x, y, z – айнымалы шамалар z – ке әртүрлі мән беріп, бұл теңдеудің осы z – тің мәндеріне сәйкес геометриялық мағынасын қарастырайық.
1. 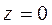 ,
, 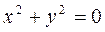 . Бұл теңдеу х пен у ноль болғанда қанағаттанады. Сондықтан z ноль болғанда х пен у-те ноль болады, яғни конустық беттің төбесі координаталардың бас нүктесінде жатады.
. Бұл теңдеу х пен у ноль болғанда қанағаттанады. Сондықтан z ноль болғанда х пен у-те ноль болады, яғни конустық беттің төбесі координаталардың бас нүктесінде жатады.
2. 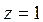 ,
, 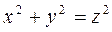 . Конустық бетті
. Конустық бетті 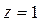 жазықтығы қиып өткенде оның қимасы шеңбер болады, яғни
жазықтығы қиып өткенде оның қимасы шеңбер болады, яғни 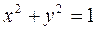 , ал
, ал 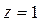 жазықтығы хОу жазықтығына параллель.
жазықтығы хОу жазықтығына параллель.
Егер 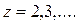 болса, онда
болса, онда
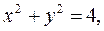
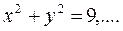
z – тің мәні өскен сайын конустың қимасындағы шеңбер өсе береді. z – ке теріс мәндерді 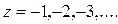 берсек, онда конустың қималары координаталардың бас нүктесінің төменгі жағында болады (169-сызба).
берсек, онда конустың қималары координаталардың бас нүктесінің төменгі жағында болады (169-сызба).
3. Егер конустың 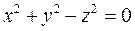
 теңдеуінде
теңдеуінде 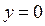 болса, онда
болса, онда
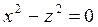 ,
, 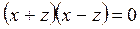 ,
,
осыдан 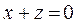 ,
, 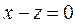
немесе 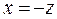 ,
, 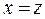 . Бұл
. Бұл
жағдайда конустық бет 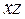
жазықтығымен мына екі 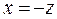 ,
,
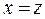 түзуінің бойымен қиылысады.
түзуінің бойымен қиылысады.
4. Егер 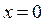 болса, онда
болса, онда
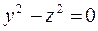 ,
, 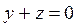 ,
, 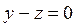
немесе 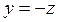 ,
, 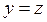 . Мұнда
. Мұнда 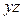
жазықтығы конусты екі 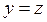 ,
,
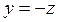 түзуінің бойымен қияды.
түзуінің бойымен қияды.
Бұл жағдайдағы конустың жасаушы
теңдеуі мынадай:
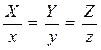 .
.
169-сызба Конустық беттің
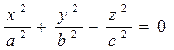 теңдеуін зерттесек, онда да жоғарғыдай қорытынды болады. Мұндағы
теңдеуін зерттесек, онда да жоғарғыдай қорытынды болады. Мұндағы
айырма конустық беттің перпендикулярлық қимасындағы бағыттаушы қисық – эллипс. Сонымен, екінші ретті конустық бет тік бұрышты координаталар системасында мынадай теңдеулермен анықталады:
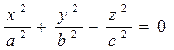 ,
,
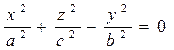 , (13)
, (13)
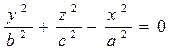 .
.
1-есеп. 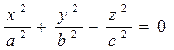 теңдеуі берілген.
теңдеуі берілген. 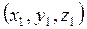 конустың бойындағы берілген нүкте болсын. Осы нүктеден конусқа жүргізілген жанаманың теңдеуін табайық.
конустың бойындағы берілген нүкте болсын. Осы нүктеден конусқа жүргізілген жанаманың теңдеуін табайық.
Шешуі.
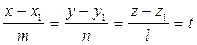 ,
,
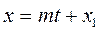 ,
,
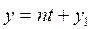 ,
,
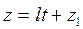 ,
,
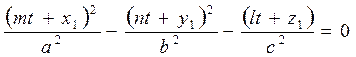 .
.
Бұл t параметрінің мәніне байланысты квадрат теңдеу болады. Осы квадрат теңдеудің түбірлері бірдей болу үшін мынадай шарт орындалады:
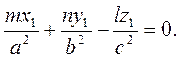
Сондықтан осы теңдеу мен мына
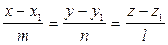
теңдеуінен 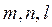 параметрлерін шығарсақ, онда конусқа жүргізілген жанама түзудің теңдеуін табамыз:
параметрлерін шығарсақ, онда конусқа жүргізілген жанама түзудің теңдеуін табамыз:
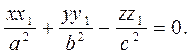 (14)
(14)
2-есеп. Төбесі координаталардың
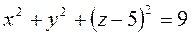 ,
,
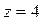 ,
,
анықталатын конустың теңдеуін табайық.
Шешуі. Конустың жасаушы теңдеуінен
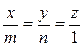
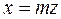 ,
, 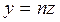 ,
, 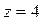 .
.
Осы x, y, z – тің мәндерін жоғарғы теңдеуге қояйық:
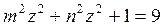 ,
,
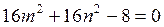 ,
,
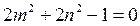 .
.
Енді конустың теңдеуін табайық:
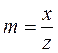 ,
, 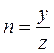 ,
,
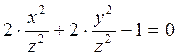 ,
,
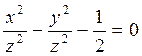 ,
, 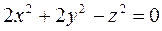 .
.
§ 4. Эллипсоид. Эллипсоид деп мынадай
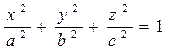 (15)
(15)
теңдеуімен анықталатын геометриялық бетті айтамыз. Бұл теңдеуді қарастырудан бұрын мына мәселеге тоқталайық. Кеңістіктегі геометрияда айналмалы геометриялық беттер жиі кездеседі. Мысалы: айналмалы цилиндр, айналмалы конус немесе айналмалы эллипсоид. Қысқаша айтқанда, айналмалы екінші ретті бет дегеніміз не?
Айналмалы бет деп бір берілген түзудің немесе қисық сызықтың берілген түзуден айнала қозғалуынан шыққан бетті айтамыз. Бұл
айналмалы бет қозғалғанда,
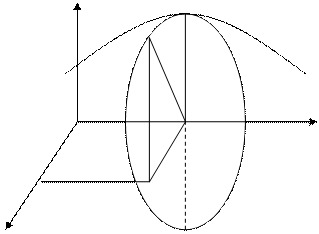 оның әрбір нүктесі шеңбер
оның әрбір нүктесі шеңбер
сызады. Берілген түзу сол
шеңбердің жазықтығына
әрқашанда перпендикуляр
болады және оның центрінен
өтеді. Бұл түзу айналу осі
деп аталады.
хОу жазықтығында бір (L)
сызығы бізге мынадай
F(X,Y)=0 теңдеуімен
берілсін. Осы (L) сызығының
абсцисса осінен айналғанда
170-сызба шығатын беттің теңдеуін
іздейік.
Тік бұрышты координаталар системасында (L) сызығын жүргізейік (170-сызба). Айналмалы беттегі кез келген бір 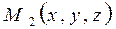 нүктесін алып, одан абсцисса осіне
нүктесін алып, одан абсцисса осіне 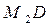 перпендикулярын жүргізейік. Одан кейін
перпендикулярын жүргізейік. Одан кейін 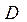 нүктесінен хОу жазықтығындағы Ох осіне перпендикуляр орнатайық. Осы перпендикулярдың берілген (L) сызығымен қиылысатын нүктесі
нүктесінен хОу жазықтығындағы Ох осіне перпендикуляр орнатайық. Осы перпендикулярдың берілген (L) сызығымен қиылысатын нүктесі 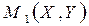 болсын. Бұл нүктенің Ох осінен қашықтығы
болсын. Бұл нүктенің Ох осінен қашықтығы 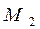 нүктесінің осы осьтен қашықтығындай болады:
нүктесінің осы осьтен қашықтығындай болады: 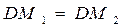 .
. 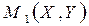 нүктесі (L) сызығының бойында жатқандықтан, оның координаталары мына берілген F(X,Y)=0 теңдеуін қанағаттандырады:
нүктесі (L) сызығының бойында жатқандықтан, оның координаталары мына берілген F(X,Y)=0 теңдеуін қанағаттандырады: 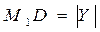 ,
, 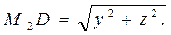
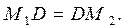
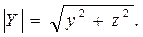
Сондықтан
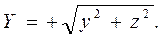
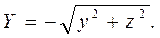
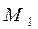 ,
, 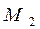 ,
, 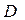 - нүктелері yOz жазықтығына параллель жазықтықта жатқандықтан, x=X.
- нүктелері yOz жазықтығына параллель жазықтықта жатқандықтан, x=X.
Ендеше, мына F(X,Y)=0 теңдеуіндегі Х пен У – тің орнына x=X, 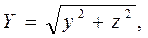
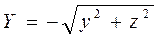 қойып мынаны табамыз:
қойып мынаны табамыз:
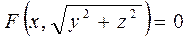 ,
,
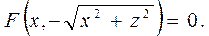
немесе
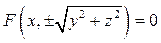 (16)
(16)
Сөйтіп, ХОУ жазықтығындағы Ғ(х, у) теңдеуімен берілген бір (L) сызығы ОХ осінен айналса, онда айналмалы беттің теңдеуі мынадай болады:
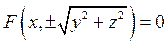
мұндағы х, у, z – кеңістіктегі нүктенің координаталары, Ох осі ОХ осімен, Оу осі ОУ осімен үйлеседі. 1-мысал. Түзудің хОу жазықтығында у = х теңдеуі берілсін. Егер осы түзуді Ох осінен айналдырсак, онда (16) формула бойынша мынадай теңдеу шығады:
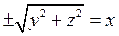
немесе
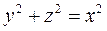 ,
,
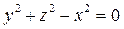 .
.
Бұл - төбесі координаталардың бас нүктесінде жатқан конустық беттің теңдеуі. Сонымен, у = х биссектрисасының абсцисса осінен айналғаннан шықкан кеңістіктегі геометриялық бейнесі конус болады. Оның теңдеуі:
2-Мысал. Егер хОу жазықтығындағы х2 + у2 = R2 шеңберін абсцисса осінен айналдырсақ, онда айналмалы бет сфера болады. Оның теңдеуі 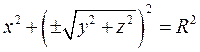 формуласы бойынша былай жазылады:
формуласы бойынша былай жазылады:
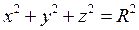 .
.
Егер 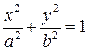 ,
, 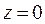 эллипсті Ох осінен айналдырсақ, онда
эллипсті Ох осінен айналдырсақ, онда
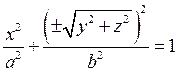
немесе
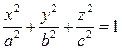
Бүл айналмалы эллипсоид деп аталады. Егер осы айналмалы эллипсоидты у осінің бойымен созсақ, онда 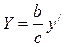 немесе у'=-үУ болады. Мұндағы b >с – кесінділер. Айналмалы эллипсоидтың теңдеуі
немесе у'=-үУ болады. Мұндағы b >с – кесінділер. Айналмалы эллипсоидтың теңдеуі 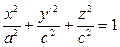 болсын.
болсын.
Енді 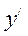 - тің мәнін осы теңдеуге қойып, эллипсоидтың теңдеуін табайык:
- тің мәнін осы теңдеуге қойып, эллипсоидтың теңдеуін табайык:
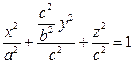
Гиперболалық параболоид.
Тік бүрышты координаталар системасында
х2 у2
_____ ― ______ = 2z
р q
теңдеуімен кескінделетін екінші ретті бетті гиперболалық параболоид деп атаймыз. Мұнда р > 0, q > 0. Берілген тендеудегі х, у ағымдық координаталық екінші дәрежелі болғандықтан, бұл екінші ретті бет у z,
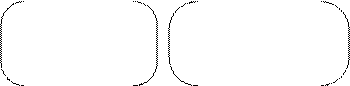 хz жазыктықтарына және О zапликата осіне қарағанда симметриялы болады. Екінші ретті беттің ху жазықтығымен қиылысатын сызығын анықтау үшін z-ті нольге тең деп алайык. Енді теңдеу былайша түрленеді:
хz жазыктықтарына және О zапликата осіне қарағанда симметриялы болады. Екінші ретті беттің ху жазықтығымен қиылысатын сызығын анықтау үшін z-ті нольге тең деп алайык. Енді теңдеу былайша түрленеді:
х2 у2 х у х у
_____ ― ______ = 0, ________ + ________ ________ ― ________ = 0,
2р 2q 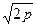
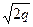
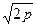
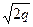
х у
________ + ________ = 0,
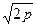
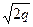
(І)
х у
________ + ________ = 0.
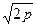
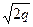
Бұл теңдеулер ху жазықтығындағы екі түзуді кескіндейді, Бұл түзулер координаталардың бас нүкгесінен өтеді және Ох, Оу осьтеріне симметриялы болады. Гиперболалык параболопдка z = Һ жазықтығын жүргізсек, онда оның ху жазыктығындағы параллель қимасы гипербола болады:
х2 у2 х2 у2
_____ ― ______ = h; _____ ― ______ = 1 (ІІ)
2 р 2 q 2 рh 2h
Гиперболаның жарты осьтері а1= 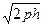 , b1 =
, b1 = 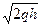 . Гипербола төбелерінің арасы 2а = 2
. Гипербола төбелерінің арасы 2а = 2 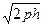 . h өскен сайын гипербола осі өсіп отырады. Бұл жағдайда гиперболалык параболоид ху жазыктығының үстінде, Ох осінің бағытымен шексізге дейін кетеді. h азапған сайын қима жазықтығы төмендей береді. z = Һ = 0 болғанда қима жазықтығы ху жазықтығымен беттеседі.
. h өскен сайын гипербола осі өсіп отырады. Бұл жағдайда гиперболалык параболоид ху жазыктығының үстінде, Ох осінің бағытымен шексізге дейін кетеді. h азапған сайын қима жазықтығы төмендей береді. z = Һ = 0 болғанда қима жазықтығы ху жазықтығымен беттеседі.
Егер екінші ретті бетті z = - Һ жазықтығымен қисақ, онда оның қимасындағы сызық тағы да гипербола болады:
х2 у2
_____ ― ______ = - h
2 р 2 q
немесе
х2 у2
_____ ― ______ = 1. (ІІІ )
2 q h 2р h
Бұл гиперболадағы нақты жарты ось b1 = 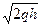 , жорымал жарты ось а1 =
, жорымал жарты ось а1 = 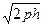 .
.
Екінші (ІІ) теңдеу мен үшінші (ІІІ)теңдеудің айырмасы, олардың осьтерінін алмасатындығында.
h өскен сайын z =—h жазыктығы төмендейді. хг жазықтығы гиперболалық параболоидты х2 = 2р zпараболаның бойымен қияды,
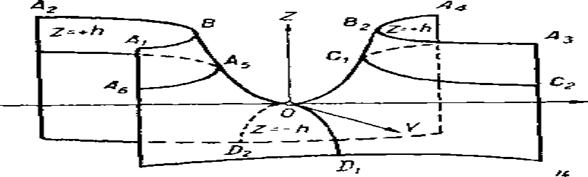
179-сызба.
яғнн егер у = 0 болса. онда у2 = 2р zболады. Егер х = 0 болса, онда у2 = — 2 q z болады.
Осы шыккан қорытындыларды пайдаланып гиперболалық параболоидтың графигін салуға болады 179-сызбада z =+h гипербола-
 |
 |
 |
 |
 |
 |
 |
 |
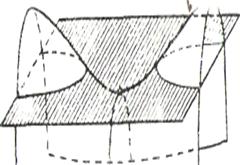
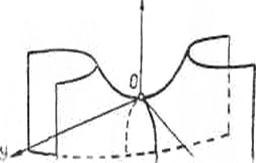
а б
180-сызба. 180-сызба.
лық қисықтар. 180. а-сызбада пшерболалык параболоидка жүргізілген жазыктыктын кпмалары. ал 180, б-сызбада гиперболалық параболоидтың сырткы пішіні көрсетілген. 179-сызбадағы қималар: гиперболалар —.А2В1-А1,.А1.А5.А6. А4В2А3, А3С1С2; параболалар — В1ОВ2, D1ОD2.
§ 9.Гиперболалық параболоидтың түзу сызықты жасаушылары. Гиперболалық параболоидтың түзу сызықты жасаушыларының теңдеулерін шығару үшін, гиперболалық параболоидтың теңдеуін түрлендірейік:
х2 у2
_____ ― ______ = z, (25)
2р 2q
 |  |
х у х у
________ + ________ ________ ― ________ = z.
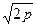
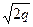
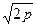
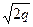
Осыдан екі теңдеулер системасын құрайық:
х у
 ________ + ________ = k1
________ + ________ = k1
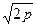
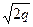
х у 1
________ + ________ = ________ z
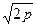
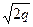 k1
k1
 х у
х у
________ + ________ = k2
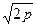
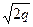
х у х
________ + ________ = ________ z.
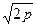
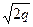 k2
k2
мұндағы k1 k2 ― еркінше алынған сандар ― параметрлер.
Осы теңдеулердің әрқайсысы жазықтықты кескіндейді, екі (І), (ІІ) теңдеудің жиындылары екі түзуді береді. Бұл түзулер гиперболалық параболоидтың түзу сызықты жасаушылары деп аталады (181 және 182-сызбалар). Осы (І), (ІІ) теңдеулеріндегі х, у, z ағымдық координаталардың мәндері гиперболалық параболоидтың теңдеуін қанағаттандырады. Сондықтан түзу сызықты жасаушылар гиперболалық параболоидтың бетінде жатады. Бір қуысты гиперболоид сияқты гиперболалық параболоидтың әрбір нүктесінен екі
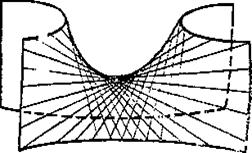
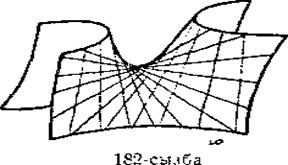
181-сызба. 182-сызба.
түзу сызықты жасаушылар өтеді, оның біреуі әрқашанда бірінші системадан болса, ал екіншісі әрқашанда екінші системадан болады (181 және 182-сызбалар). Бір системаның түзулері өз ара қиылыспайды. Сейтіп, мұнда екі түрлі түзулер үйірімі болады. Бұл түзулердің біреуі бірінші системамен (І), екіншісі екінші (ІІ) системамен кескінделеді. k1 және k2 параметрлерінің мәндеріне байланысты түзулер үйірімінің осыларға сәйкес теңдеулері шығады. Берілген есептің шарты бойынша k1 және k2 параметрлердің мәндерін табуға болады. Табылған теңдеулері арқылы гиперболалық параболоидтың түзу сызықты жасаушыларының тік бұрышты координаталар системасында қандай болып өтетінін карастыру киын емес.
Мысал.Мына Зх — 2у — 4z = 0 жазықтығында параллель болатын
х2у2
— - — = 2 гиперболалык параболоидтың түзу сызықты
8 2
жасаушыларын табайық.
Ш е ш у і.
х2 у2 х2 у2
_____ ― ______ = 2 z, _____ ― ______ = z,
2 2 4 2

 х2 у2 х2 у2
х2 у2 х2 у2
_____ + ______ _____ ― ______ = z.
4 2 16 4
Осыдан
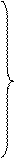 х у
х у
_____ + ______ = k
4 2
х у z
_____ - ______ = ______
4 2 k
Бұл екі теңдеуді қолайлы түрге келтіру үшін әуелі оларды косайық, сонан кейін бірінен-бірін алайық. Сонда
х z х-2 k z
_____ = k + ______ , ____ ______ = ______,
4 k 2 k
у у z z
_____ + ______ = k - ______, у – k = - ______,
2 2 k k
z х-2k k-у z
k - у= ______, ______ = ______ = ______.
k 2 1 k
Есептің шарты бойынша бұл түзу берілген Зх — 2у —4г = 0 жа-зыктығына параллель. Сондықтан
3 • 2 — 2 • 1—4• k = 0, 6-2-4 k = 0, k =1.
Гиперболалық параболоидтың түзу сызықты жасаушыларының біреуінің теңдеуі
Х -2 у -1 z
______ = ______ = ______.
2 -1 1
Енді екінші теңдеуін табайық:
х у
— - — = l
4 2
х у z
— + — = —
4 2 l
Осы екі теңдеуді әуелі қосайык, сонан кейін бір-бірінен алып тастайық. Сонда
х z х-2 l z
_____ = L + ______ , ____ ______ = ______,
2 l 2 l
z z
- у= l- ______, y+l= ______,
l l
x-2l у+ l z
_____ = ______ = ______,
2 1 l
Түзу мен жазықтықтың параллельдік шарты бойынша параметрін тауып, іздеген екінші жасаушы түзудің теңдеуін жазанық:
6-2-4 l = 0, l =1;
x - 2 у+ 1 z
_____ = ______ = ______.
2 1 1
§10.Екінші ретті беттің дөңгелектік қималары.
Егер екінші ретті бетке жазықтық жүргізгенде оның қимасы  шеңбер болса, онда мұндай қиманы екінші ретті беттің дөңгелектік қимасы дейміз. Екінші ретті беттің нүктелерінде жанама жазықтықтар дөңгелектік қималарға параллель болса, онда мұндай нүктелерді дөңгелену нүктелері дейміз. Ең алдымен екінші ретті беттің дөңгелектік қима-ларының теңдеулерін қорытып шығарайық. Сонан кейін дөңгелену.нүктелерінің координаталарын табатын формулаларды келтірейік.
шеңбер болса, онда мұндай қиманы екінші ретті беттің дөңгелектік қимасы дейміз. Екінші ретті беттің нүктелерінде жанама жазықтықтар дөңгелектік қималарға параллель болса, онда мұндай нүктелерді дөңгелену нүктелері дейміз. Ең алдымен екінші ретті беттің дөңгелектік қима-ларының теңдеулерін қорытып шығарайық. Сонан кейін дөңгелену.нүктелерінің координаталарын табатын формулаларды келтірейік.
1) Әуелі эллипсоидтың теңдеуін алайық:
x2 у2 z2
_____ + ______ + ______ - 1= 0
а2 b2 с2
Енді координаталардың бас нүктесінен ететін шардың
x2 у2 z2
_____ + ______ + ______ - 1= 0
R2 R2 R2

 теңдеуін эллипсоидтың теңдеуінен алсақ, онда мынадай теңдеу шығады:
теңдеуін эллипсоидтың теңдеуінен алсақ, онда мынадай теңдеу шығады:
 1 1 1 1 1 1
1 1 1 1 1 1
____ - ______ x2 + ______ - ____ у2 + ______ - ______ z2 = 0 (26)
а2 R 2 b2 R2 c2 R2
Бұл теңдеу эллипсоид пен шардың қиылысатын сызығынан өтетін екінші ретті бетті сипаттайды. Дәлірек айтқанда, бұл теңдеу төбесі координаталардың бас нүктесінде болатын конустық бетті сипаттайды. Егер (26) теңдеудің коэффициенттерінің біреуі нольге тең болса, онда ол екі жазықтықтың теңдеулерін береді. Мысалы, а>b>с болғанда, мына коэффициент ноль болсын:
11
— - — = 0
c2 R2
Сонда (26) теңдеуден мынадай теңдеулерді табамыз:
1 1 1 1
(— - —)х2- (— - —)у2 = 0,
а2 с2 b2 с2
1 1 1 1
(— - —)х2 – (— - —) у2 = 0
а2 с2 b2 с2
немесе
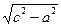
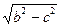
——— х = ——— = 0. (27)
а b
Қойылған шарт бойынша а>b>с. Сондықтан эллипсоидтың бұл қималары жорымал болады.
Енді 11
— - — = 0
b2 R2
болса,онда (26) теңдеуді жоғарғыдай түрлендіріп, мынаны табамыз:
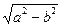
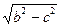
———x = ——— z = 0,
b c
мұндағы а >b> c болғандықтан,(28) қималар нақты болады.Бұл жазықтықтар екінші ретті бетті шеңбердің бойымен қияды.
Сонымен, (26) теңдеуден жазықтықтардың дөңгелектік қималарының үш түрлі теңдеуі шығады:
1 1 1 1 1 1
— = —, (— - —)х2 + (— - —)у2 = 0, (27)
с2 R2 а2 с2 b2 c2
1 1 1 1 1 1
— = —, (— - —)x2 + (— - —)z2 = 0, (28)
b2 R2 a2 b2 c2 b2
1 1 1 1 1 1
— = —, (— - —)y2 + (— - —)z2 + 0. (29)
a2 R2 b2 a2 c2 a2
Осылардың әрқайсысы дөңгелектік екі қима жазықтықтарды береді.Ал а>b>с болғандықтан,дөңгелектік нақты жазықтықтар (28) теңдеулермен сипатталады,яғни (28) теңдеу нақты қималарды көрсетеді,қалған (27 және 29) теңдеулер жорымал қималарды береді.Сөйтіп (28) теңдеулер мына екі теңдеуден құрылған:
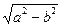
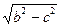
——— x + ——— z = 0, (28')
a c
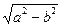
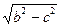
——— x - ——— z = 0.
a c
Енді (28) теңдеулерінің екі жазықтығына параллель жазықтықтар былайша жазылады:
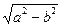
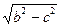
———х + ——— + u1 = 0,
а с
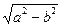
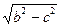
——— х - ——— + u2 = 0, (30)
а с
Бұл (30) жазықтықтар — эллипсоидтың ценгрінен ететін (28') жазықтыктарына параллель болатын жазықтықтар. Мұндағы u1 және u2 кез келген параметрлерді көрсетеді.
Сонымен, қорыта келгенде эллипсоидтың центрінен өтетін дөнгелектік жазықтықтарға параллель болатын кез келген жазықтықтар эллипсоидтың деңгелектік қималары болады.
Бір қуысты гиперболидтың дөңгелектік қималарының теңдңулері де осы әдіспен шығады.Оның дөңгелектік қималарының нақты жазықтықтары мынадай болады:
1 1 1 1
(— - —)y2 – (— + —)z2 = 0
b2 a2 c2 a2
немесе
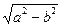
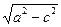
——— y Ғ ——— z = 0. (30')
b c
Бір қуысты гиперболаның бұдан басқа дөңгелектік қималары жорымал болады.
Екі қуысты гиперболоидтың дөңгелектік қималарының нақты жазықтарының теңдеулері:
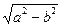
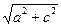
——— y Ғ ——— z = 0.
b c
(30') жазықтықтарына пареллель қима жазықтықтар мынадай болады:
у z
— 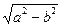 + —
+ — 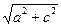 +u1 = 0,
+u1 = 0,
b c
y z
— 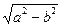 - —
- — 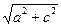 + u2= 0, (30'')
+ u2= 0, (30'')
b c
мұндағы a > b.Енді
х2 y2
—— + —— - 2z = 0
p q
эллипстік параболидты алайық.Мұның төбесінен өтетін бір
х2 + у2 + (z – R)2 – R2 = 0
шарды алып,оның теңдеуіне сәйкес эллипстік параболидтың теңдеуін алсақ, онда мынадай теңдеу шығады:
1 1 1 1 z2
(— - —)x2 + (— - —)y2 + — = 0. (31)
R2 p R2 q R
Шардың теңдеуін былайша жазуға болады:
х2 + у2 + (z- R)2 – R2 = 0
немесе
х2 y2 z2
— + — + — - 2z = 0.
R R R
(31) теңдеудегі ең соңғы мүше
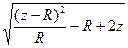 =
= 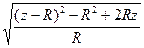 =
= 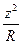 .
.
(31) теңдеуі шар мен параболидтың қиылысатын сызығынан өтетін және төбесі координаталардың басында жатқан конустық бетті сипаттайды.(31) теңдеудің сол жағындағы коэфициенттер
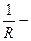
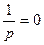 ,
, 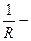
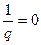 болса, онда конус екі жазықтыққа айналады.Егер p>q және
болса, онда конус екі жазықтыққа айналады.Егер p>q және 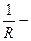
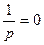 болса, онда дөңгелектік қималардың теңдеуі мынадай болады:
болса, онда дөңгелектік қималардың теңдеуі мынадай болады:
у2(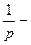
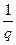 ) +
) + 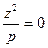 , (31')
, (31')
мұндағы 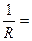
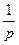 ,
, 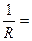
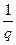 .
.
(31') теңдеуі —екі дөңгелектік жазықтықтың теңдеулері. Олар мынадай түрде жіктеледі:
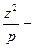 (
(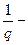
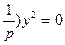 , (
, (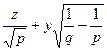 )
) 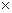 (
(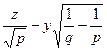 ) = 0
) = 0
немесе
(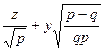 )(
)(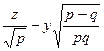 ) = 0. (31'')
) = 0. (31'')
Осы жазықтықтарға параллель жазықтықтар эллипстік параболоидты шеңбердің бойымен қияды, яғни бұл теңдеулер параболоидтың дөңгелектік екі қимасын сипаттайды. Соңғы (31'') теңдеуді 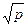 -ға қысқартып,жекелеп жазсақ,мынадай болады:
-ға қысқартып,жекелеп жазсақ,мынадай болады:
у 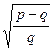 +z = 0,
+z = 0,
y 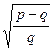 - z = 0. (31''')
- z = 0. (31''')
Енді осы жазықтықтарға параллель дөңгелектік жазықтықтардың теңдеулері былайша жазылады:
у 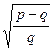 + z + u1=0, (31'''')
+ z + u1=0, (31'''')
y 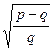 - z + u2 = 0.
- z + u2 = 0.
Мұндағы u1, u2 —параметрлер.
(31'''') теңдеулері эллипстік параболидтың дөңгелектік (қимасындағы) кез келген параллель жазықтықтарын сипаттайды.
2) Дөңгелену нүктелерінің координаталарын анықтайтын формулаларды шығарайық. Эллипсойтың жанасу нүктесінің координаталары х1,у1, z1 болсын. Онда.
хх1 уу1 z z 1
_____ + ______ + ______ - 1= 0
а2 b2 с2
жанама жазықтығы (28') тендеудің екі жазықтығына параллель болғандықтан, мына
x1 y1 z
_____: 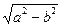 = _____: 0 = _____: Ғ
= _____: 0 = _____: Ғ 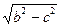
а b c
шарттар орындалады, яғни бұл — екі жазықтықтың параллельдік шарттары. Енді эллипсоидтың теңдеуі мен бұл теңдеулерді біріктіріп шығарайық:
х21 у12 z 21
_____ + ______ + ______ - 1= 0
а2 b2 с2
х1 у1 z 1
_____ ______ ______ - 1= 0,
а b с
________ = _________ ___________
V a2 – b2 0 Ғ V b2 – c2
y1 = 0, сонда
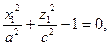
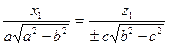
Соңғы теңдеулер системасынан:
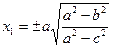 ,
,
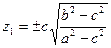 , (32)
, (32)
y1= 0.
Сөйтіп,эллипсоидтың дөңгелену нүктелерінің координаталары осы формулалармен анықталады. Екі қуысты гиперболоидтың дөңгелену нүктелерінің кординаталарын осы әдіспен табамыз:
х1= 0,
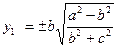 (32')
(32')
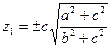 .
.
Бір қуысты гиперболоидтың нақты дөңгелену координаталары тіпті жоқ..Эллипстік параболидтың дөңгелену координаталары жоғарғы айтылған әдіспен табылады:
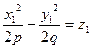 , х1=0,
, х1=0,
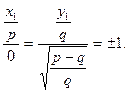
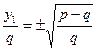
Сөйтіп,дөңгелектену нүктелерінің координаталары былай анықталады:
х2= 0,
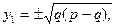
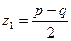 , (32'')
, (32'')
мұндағы p>q. р және q раметрлерінің сандық мәндері берілсе,дөңгелену координаталары осы (32'') формуласымен табылады.
1-мысал. Мына 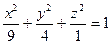 эллипсоидтың дөңгелену нүктелерін табайық..
эллипсоидтың дөңгелену нүктелерін табайық..
Шешуі. (32) формула бойынша:
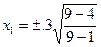 =
= 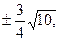 z1=
z1= 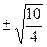 , y1= 0.
, y1= 0.
M1(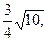 0,
0, 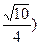 , M1(-
, M1(- 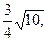 0, -
0, - 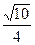 ).
).
2-мысал. Мына 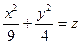 эллипстік параболоидтың дөңгелену нү
эллипстік параболоидтың дөңгелену нү
 2015-04-12
2015-04-12 5737
5737








