Понятие прямой линии – первичное в геометрии. Свойства прямой определяются аксиомами геометрии. Геометрически построить линию можно разными способами:
Задать две точки на плоскости.
Задать одну точку M 0(x 0; y 0) и направляющий вектор a.
Задать одну точку M 0(x 0; y 0) и нормальный вектор n.
Задать одну точку и угол наклона к оси Ox.
Каждому из этих способов задания линии соответствует своя форма уравнения прямой.
| № | Название | Вид уравнения | Дано |
| Каноническое уравнение прямой | 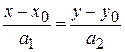
| Точка M 0(x 0; y 0) и направляющий вектор a = { a 1; a 2} | |
| Уравнение прямой, проходящей через две точки | 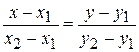
| Две точки M 1(x 2; y 2), M 0(x 2; y 2) |
| № | Название | Вид уравнения | Дано |
| Уравнение прямой в отрезках | 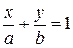
| Две точки M 1(a; 0), M 2(0; b) | |
| Общее уравнение прямой | 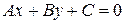 где
где 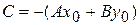
| Точка M 0(x 0; y 0) и нормальный вектор n = { A; B } | |
| Уравнение прямой с угловым коэффициентом | y = kx + b | Угол пересечения оси
Ох – 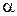 .
Смещение по ординате – b
k = tg .
Смещение по ординате – b
k = tg 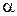 = = 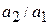
|
 2015-04-12
2015-04-12 647
647








