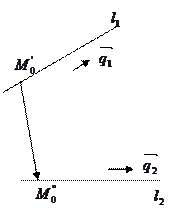 Пусть
Пусть 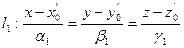 ;
; 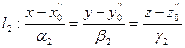 .
.
 и
и  либо пересекаются, либо параллельны (в частном случае совпадают), либо скрещиваются.
либо пересекаются, либо параллельны (в частном случае совпадают), либо скрещиваются.
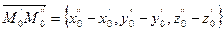 . В случае если
. В случае если 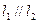 или пересекаются, существует плоскость, которой прямые принадлежат. Поэтому выполняется условие:
или пересекаются, существует плоскость, которой прямые принадлежат. Поэтому выполняется условие:
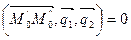 . (18)
. (18)
Утверждение 7. Прямые  и
и 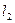 скрещиваются тогда и только тогда, когда
скрещиваются тогда и только тогда, когда
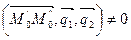 . (19)
. (19)
1) Если прямые пересекаются, то может решаться задача нахождения угла между прямыми. В этом случае угол определяется углом между направляющими векторами.Если прямые параллельны, то возникает задача нахождения расстояния между ними:
Плоскость, содержащая параллельные прямые, имеет вектор нормали 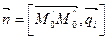 ,
, 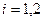 , тогда
, тогда 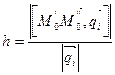
Замечание: A) 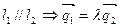 , т.е.
, т.е. 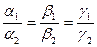 , B)
, B) 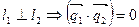 , т.е.
, т.е. 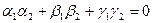 .
.
2) Если прямыескрещиваются, то расстояние между ними равно высоте параллелепипеда, построенного на векторах 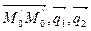 , т.е.
, т.е. 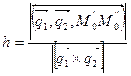
 2015-04-12
2015-04-12 486
486








