Поскольку пересекающиеся плоскости пересекаются по прямой, то
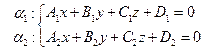 (10)
(10)
причем 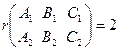 (11)
(11)
Система уравнений (10) с условием (11) называется общим уравнением прямой в пространстве. Данная система линейных неоднородных уравнений совместна и имеет общее решение следующего вида:
| (12) | 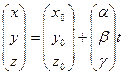 , ,
|
где 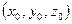 – частное решение (10),
– частное решение (10), 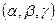 – фундаментальная система решений соответствующей системы линейных однородных уравнений.
– фундаментальная система решений соответствующей системы линейных однородных уравнений.
Геометрически (12) означает следующее:
Пусть точка 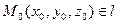 . Любая точка
. Любая точка 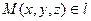 получается прибавлением к радиус-вектору точки
получается прибавлением к радиус-вектору точки 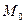 некоторого вектора, коллинеарного
некоторого вектора, коллинеарного 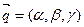 - направляющего вектора прямой.
- направляющего вектора прямой.
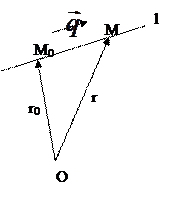
Уравнение (12) можно переписать в виде 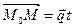 или
или
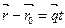 , (13)
, (13)
– векторно-параметрическое уравнение прямой 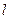 или
или
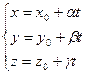 (14)
(14)
– параметрические уравнения прямой в пространстве.
Исключая параметр 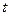 , получим:
, получим:
| (15) | 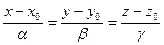
|
– канонические уравнения прямой в пространстве.
Здесь равенства (15) следует воспринимать как пропорцию.
Пример 3. Пусть прямая задана каноническими уравнениями
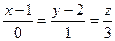 (*). Тогда уравнения (*) равносильны системе:
(*). Тогда уравнения (*) равносильны системе:
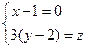 ,
,  .
.
Если необходимо написать уравнение прямой, проходящей через две точки  и
и 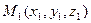 , то
, то 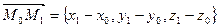 – направляющий вектор, тогда
– направляющий вектор, тогда
| (16) | 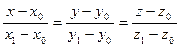
|
– уравнение  , проходящей через 2 точки.
, проходящей через 2 точки.
Утверждение 6. Если прямая 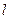 , задана как пересечение двух плоскостей системой (.10), то вектор
, задана как пересечение двух плоскостей системой (.10), то вектор
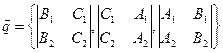 (17)
(17)
– является направляющим вектором 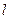 , т.е.
, т.е. 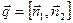 .
.
 2015-04-12
2015-04-12 441
441








