1. Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей.
2. В равнобедренном ∆ DEK c основанием DK, отрезок ЕF – биссектриса,
DK = 16 см, 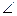 DEF = 430. Найдите KF,
DEF = 430. Найдите KF, 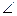 DEK,
DEK, 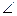 EFD.
EFD.
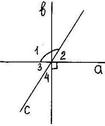
3. Дано: а 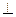 b,
b, 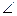 1 = 1250. Найдите
1 = 1250. Найдите 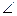 2,
2, 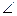 3,
3, 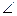 4.
4.
Билет № 8
1. Определение треугольника. Теорема о сумме углов треугольника.
2. Найдите углы равнобедренного треугольника, если угол при основании в 3 раза меньше внешнего угла, смежного с ним.
3. В ∆ RPQ  P = 900, RS – биссектриса и равна 15,6 см, PS = 7,8 см. Найдите SQ и
P = 900, RS – биссектриса и равна 15,6 см, PS = 7,8 см. Найдите SQ и 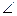 RQT.
RQT.
Билет № 9
1. Определение внешнего угла. Свойство внешнего угла.
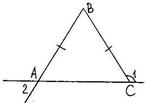
2. На рисунке АВ = ВС,  1 = 1300. Найдите
1 = 1300. Найдите  2.
2.
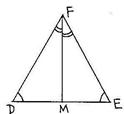
3. В ∆ DEF  D =
D = 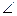 E, DF + FM + DM = 28 м. Периметр ∆ DEF равен 36 м. Найдите FM.
E, DF + FM + DM = 28 м. Периметр ∆ DEF равен 36 м. Найдите FM.
 2015-04-12
2015-04-12 2505
2505








