Сабақ №27 Өтілу мерзімі: 12.12.12
Сабақтың тақырыбы: Конустың жазбасы, бетінің ауданы
Сабақтың мақсаты:
І. БІЛІМДІЛІК. Оқушыларға конус туралы түсінік беріп, конустың жазбасы мен бүйір және толық бетінің ауданын қарастыру.
ІІ. ТӘРБИЕЛІК. Оқушыларды ұқыптылыққа, тиянақтылыққа, шапшаңдыққа баулу.
ІІІ. ДАМЫТУШЫЛЫҚ. Ойлау қабілеттерін дамыту.
Сабақтың түрі: жаңа сабақ
Оқыту әдісі: сұрақ-жауап, баяндау
Сабақтың көрнекілігі: циркуль, сызғыш, конустың моделі.
Сабақ барысы:
1.Ұйымдастыру кезеңі. Оқушылардың сабаққа дайындығын байқау, түгендеу
ІІ. Үй жұмысын тексеру. а) Ой қозғау(сұрақ-жауап)
1. Конустың жазықтықпен қимасында осьтік қимадан басқа тең бүйірлі үшбұрыш шығуы мүмкін бе?
2. Конустың осьтік қимасы тікбұрышты үшбұрыш болуы мүмкін бе?
ІІІ. Жаңа сабақ
Конустың жазбасы және бетінің ауданы
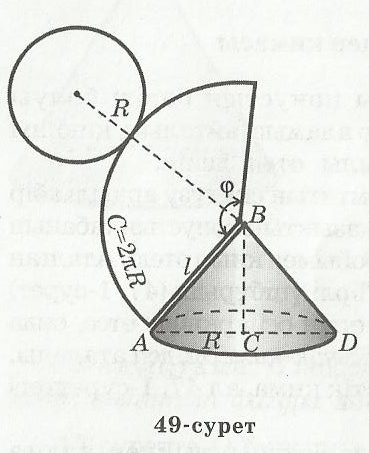
Егер конустың бүйір бетін қайсібір жасаушысының бойымен, мысалы, АВ-ның бойымен қисақ, онда конустың бүйір бетінің жазбасын аламыз (49-сурет).
Радиусы R-ге, жасаушысы l -ге тең конустың бүйір бетінің жазбасы радиусы l -ге, ұзындығы 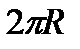 -ге тең дөңгелектің секторы болады (49-сурет).
-ге тең дөңгелектің секторы болады (49-сурет).
Мұндай жазбаның ауданы конустың бүйір бетінің ауданы ретінде қолданылады, Sк.б.б деп белгіленеді.
С –конустың табан шеңберінің ұзындығы.
Дөңгелек секторының ауданының формуласын пайдалансақ, 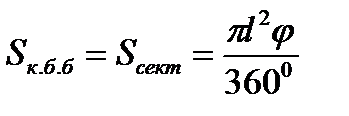 φ- сектор доғасының бұрыштық шамасы. Конустың табан шеңберінің ұзындығы φ- сектор доғасының бұрыштық шамасы. Конустың табан шеңберінің ұзындығы 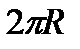 -ді сектор доғасының -ді сектор доғасының 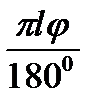 ұзындығына теңестіріп, φ доғасының бұрыштық шамасын тауып аламыз: ұзындығына теңестіріп, φ доғасының бұрыштық шамасын тауып аламыз: 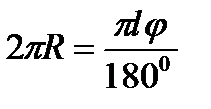 бұдан бұдан 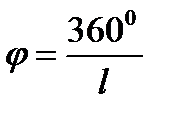 . . 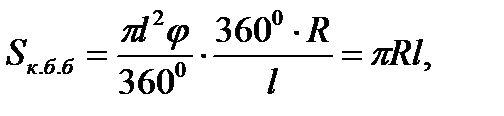 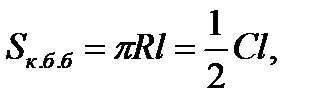 |
 |
Конустың бүйір бетінің ауданы оның табан шеңберінің ұзындығы мен жасаушысының көбейтіндісінің жартысына тең: 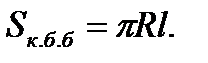
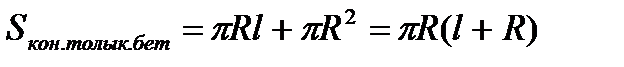 |
IV. Бекіту жаттығулары №
| А |
| В |
| О |
| S |
∆ SАВ - осьтік қима.
S қима = 12.
SA = l = 5.
Шешуі: S қима = 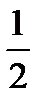 ∙ SO ∙AB =
∙ SO ∙AB = 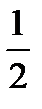 H ∙2R=
H ∙2R=
= H ∙ R = 12
S б.б. = π R l = 5 π R;
V = 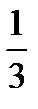 π R2 H = 4 π R;
π R2 H = 4 π R;
Орындарына осы өрнектерді қойсақ,
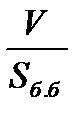 =
= 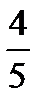 ; Жауабы:
; Жауабы: 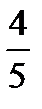 ;
;
Есеп. Конустың бүйір бетінің ауданы оның табанының ауданынан 2 есе артық. Конустың бүйір бетінің жазбасының бұрышын табыңыз.
S б.б = 2 S таб.
S б. б. = π R ℓ; ℓ = жасаушы
S таб. = π R2 ;
π Rℓ = 2π R2 ; бұдан, ℓ = 2R;
Конус жазбасы болатын сектор
доғасының ұзындығын
SA = ℓ = 2π R = 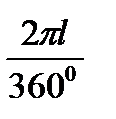
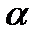 ;
;
2π R = 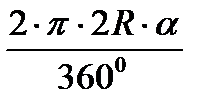 ;
;
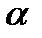 = 1800 ; Жауабы: 1800
= 1800 ; Жауабы: 1800
V. Сабақты қорытындылау:
1. Конустың қимасында тең қабырғалы үшбұрыш шығуы мүмкін бе?
2. Конустың центрі, осі немесе симметрия жазықтығы бола ма?
3. Конустығ жасаушысы: 1) конустың биіктігіне; 2) табан шеңберінің радиусына тең болуы мүмкін бе? Тұжырымды негіздеңдер.
VІ. Оқушылар білімін бағалау
VІІ. Үйге тапсырма беру: №
 2015-04-12
2015-04-12 9833
9833








