Геометрия 11 сынып. Сабақтың тақырыбы:Іштей және сырттай сызылған конустар

Сабақ №28 Өтілу мерзімі: 15.12.12

Сабақтың тақырыбы: Іштей және сырттай сызылған конустар

Сабақтың мақсаты:

І. БІЛІМДІЛІК. Оқушыларға іштей және сырттай сызылған конустар туралы түсінік беріп,есептер шығартып жаттықтыру.

ІІ. ТӘРБИЕЛІК. Оқушыларды ұқыптылыққа, тиянақтылыққа, шапшаңдыққа баулу.

ІІІ. ДАМЫТУШЫЛЫҚ. Ойлау қабілеттерін дамыту.

Сабақтың түрі: жаңа сабақ

Оқыту әдісі: сұрақ-жауап, баяндау

Сабақтың көрнекілігі: циркуль, сызғыш, конустың моделі.

Сабақ барысы:

1.Ұйымдастыру кезеңі. Оқушылардың сабаққа дайындығын байқау, түгендеу

ІІ. Үй жұмысын тексеру. а) Ой қозғау(сұрақ-жауап)

1. Конустың жазықтықпен қимасында осьтік қимадан басқа тең бүйірлі үшбұрыш шығуы мүмкін бе?

2. Конустың осьтік қимасы тікбұрышты үшбұрыш болуы мүмкін бе?

ІІІ. Жаңа сабақ

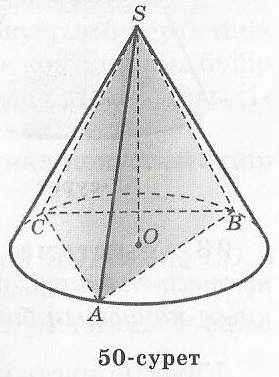50-суретте төбесі S конусқа іштей сызылған SАВС

пирамидасы бейнеленген. ∆АВС конустың табанына

іштей сызылған.

Конусқа іштей сызылған пирамидалардың бүйір

қырлары тең, себебі олар конус жасаушылары. Пирамиданың

төбесі конус табанының центріне проекцияланады. Сонымен

конустың және оған іштей сызылған пирамиданың биіктіктері беттеседі.

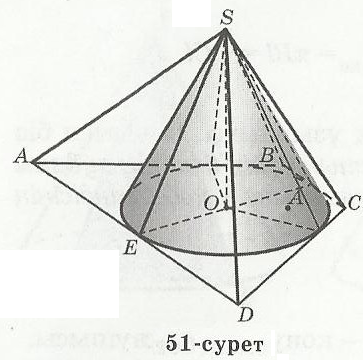51-суретте конусқа сырттай сызылған төбесі

S болатын SАВСD төртбұрышты пирамидасы кескінделген.

Байқағанымыздай, конуспен пирамиданың төбелері

беттескен, ал конустың табаны АВСD төртбұрышына

іштей сызылған.

КОНУСҚА СЫРТТАЙ СЫЗЫЛҒАН ПИРАМИДАНЫҢ ЕКІЖАҚТЫ БҰРЫШТАРЫ ТЕҢ БОЛАДЫ.

IV. Бекіту жаттығулары №

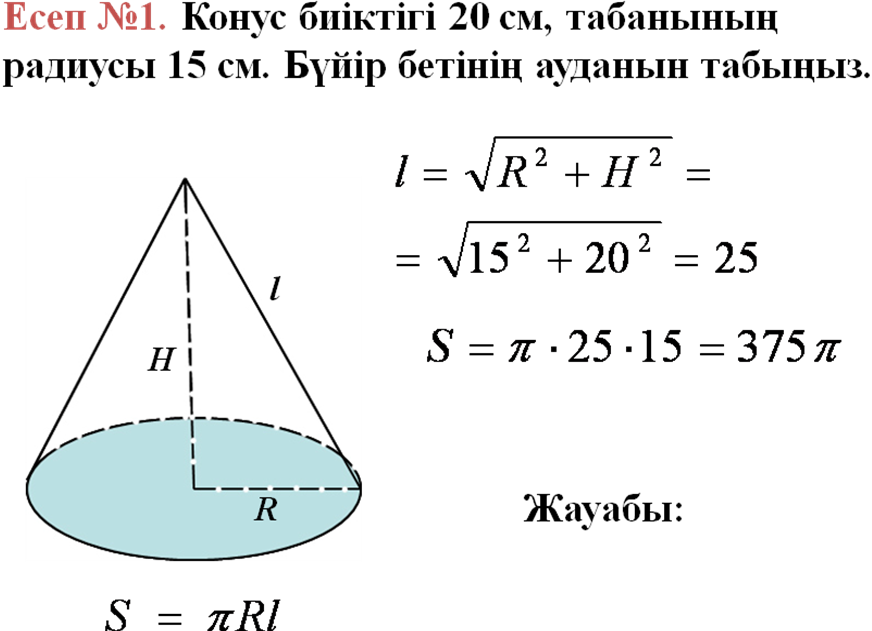
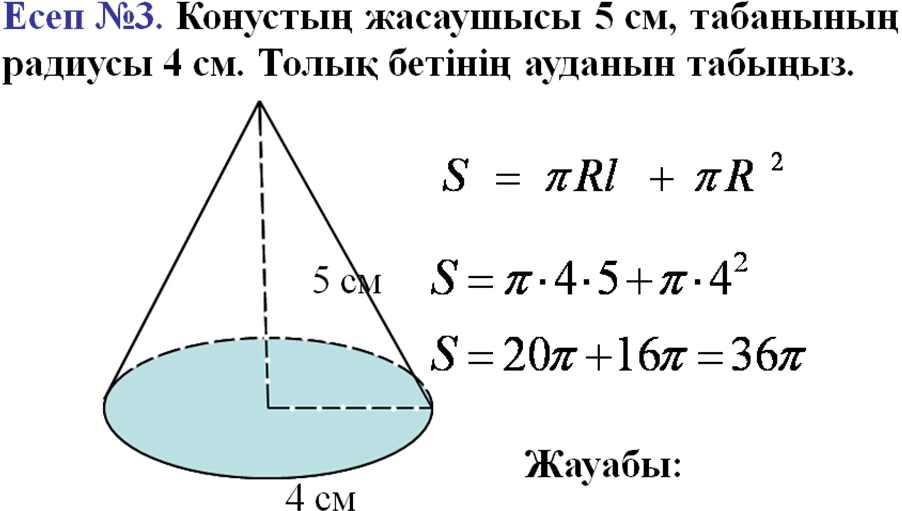
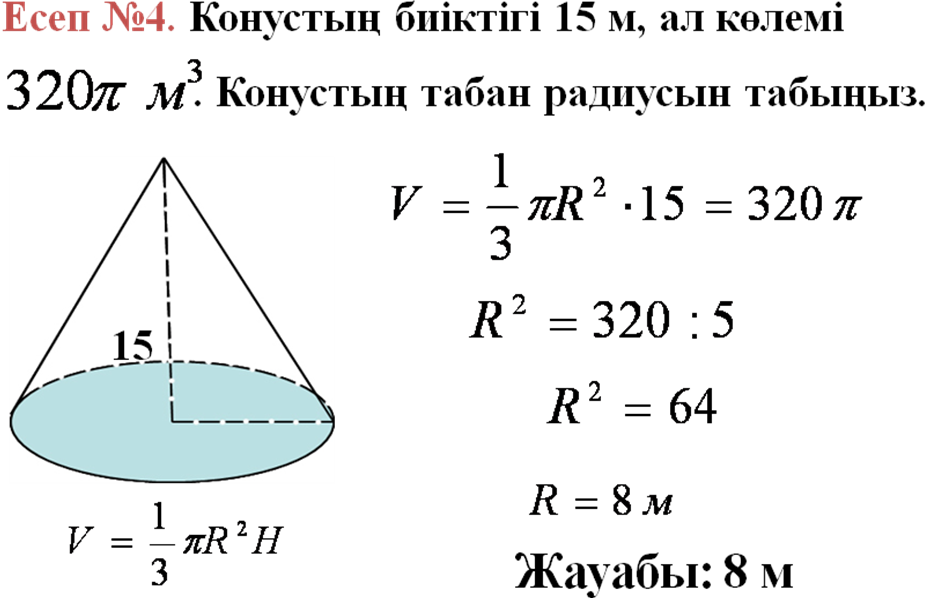
V. Сабақты қорытындылау:

1. Конустың қимасында тең қабырғалы үшбұрыш шығуы мүмкін бе?

2. Конустың центрі, осі немесе симметрия жазықтығы бола ма?

3. Конустығ жасаушысы: 1) конустың биіктігіне; 2) табан шеңберінің радиусына тең болуы мүмкін бе? Тұжырымды негіздеңдер.

VІ. Оқушылар білімін бағалау

VІІ. Үйге тапсырма беру: №