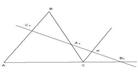
Теорема менелайя

Теорема Менелая. Пусть прямая пересекает треугольник 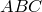, причем 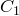– точка ее пересечения со стороной 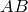, 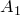– точка ее пересечения со стороно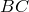й , и 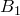– точка ее пересечения с продолжением стороны 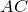. Тогда

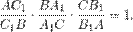Доказательство. Проведем через точку 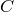прямую, параллельную 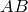. Обозначим через 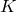ее точку пересечения с прямой .

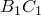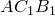Треугольники и 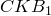подобны (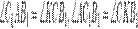). Следовательно,

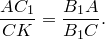Треугольник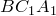и и 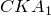также подобны ( 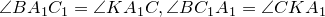Значит,

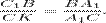Из каждого равенства выразим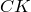

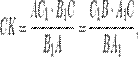откуда

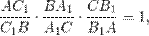что и требовалось доказать.

7 билет

1) 1. Формула площади параллелограмма через стороны и углы

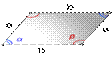
a, b - стороны параллелограмма

α, β - углы параллелограмма

Формула площади через стороны и углы параллелограмма, (S):

2. Формула площади параллелограмма через сторону и высоту

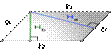
a, b - стороны параллелограмма

H _b - высота на сторону b

H _a - высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

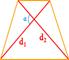
3. Формула площади параллелограмма через диагонали и угол между ними

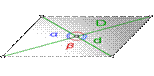
D -большая диагональ

d -меньшая диагональ

α, β - углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними, (S):

,

S = 4r2 sinα

S =   d1d2 sinα

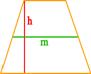	S = hm
2) S = a + b h

8 билет

1)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.