Теорема Менелая (прямая и обратная)

Теорема Менелая (ок. 100 г. н.э.). Пусть прямая пересекает треугольник ABC, причём C₁ – точка пересечения со стороной AB, A₁ – со стороной BC, B₁ – с продолжением стороны AC.

Тогда выполняется равенство:

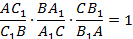
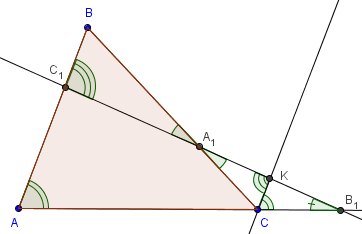Доказательство. Проведём через точку C прямую
CK параллельно AB (K – точка пересечения с C₁B₁)

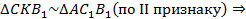
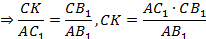
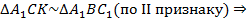
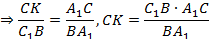
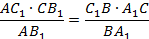
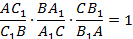
Теорема доказана.

Обратная теорема Менелая. Пусть дан треугольник ABC и точки A₁, B₁, C₁ на прямых BC, AC, BA, причём

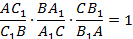
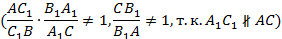
Тогда точки A₁, B₁ и C₁ лежат на одной прямой.

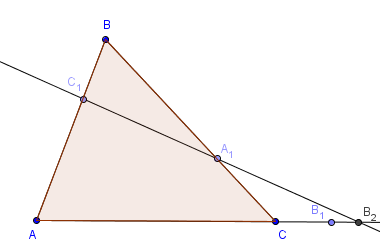Доказательство. Проведём A₁C₁. Отметим точку пересечения с прямой AC как B₂.

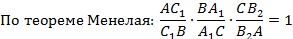
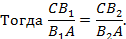
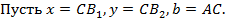
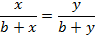
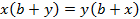
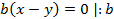
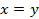Из аксиомы об откладывании отрезка следует, что B₁ совпадает с B₂.

Теорема доказана.

Билет №23