Теорема Чевы (1678 г.). Пусть точки A1, B1, C1 лежат соответственно на сторонах
BC, AC, AB. Пусть отрезки AA1, BB1 и CC1 (чевианы) пересекаются в одной точке.
Тогда:
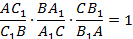
Доказательство. Пусть O – точка пересечения AA1, BB1 и CC1. Опустим из вершин A и C перпендикуляры на прямую BB1. L и K – основания перпендикуляров.
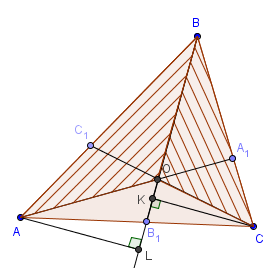
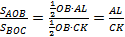
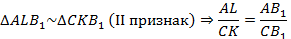
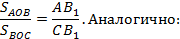

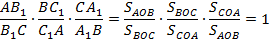
Теорема доказана.
Обратная теорема Чевы. Пусть дан треугольник ABC и точки A, B, C лежат соответственно на сторонах BC, CA, AB.
Пусть выполняется соотношение:
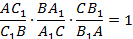
Тогда отрезки AA1, BB1, CC1 пересекаются в одной точке.
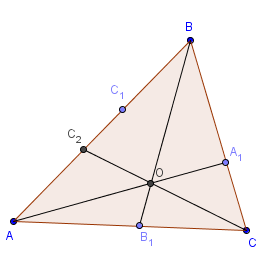
Доказательство. Пусть O – точка пересечения AA1 и BB1 и прямая CO пересекает сторону AB в точке C2. Теперь достаточно доказать, что C1 совпадает с C2.
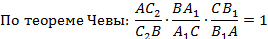
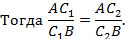
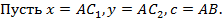
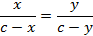
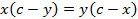
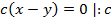
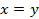
Из аксиомы об откладывании отрезка следует, что C1 совпадает с C2.
Теорема доказана.
 2015-04-12
2015-04-12 18904
18904








