2015-04-12
9674
Определение. Ромб – это параллелограмм, у которого все стороны равны.
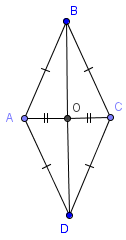Свойство 1. Диагонали ромба перпендикулярны.
Доказательство. ∆ABC – равнобедренный, BO – медиана, а значит, и высота, т.е.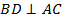 
.
Теорема доказана.
Свойство 2. Любой ромб описывается около окружности.
Доказательство. Суммы противолежащих сторон равны.
Теорема доказана.
Свойство 3. Площадь ромба равна половине произведения диагоналей.
Доказательство.
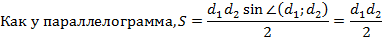
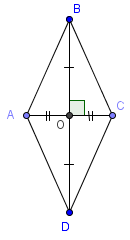Теорема доказана.
Признак 1. Если в параллелограмме диагонали взаимно перпендикулярны, то этот четырёхугольник – ромб.
Доказательство.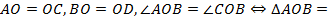 
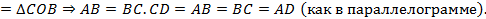
Теорема доказана.
Признак 2. Если параллелограмм описывается около окружности, то этот параллелограмм – ромб.
Доказательство. Противолежащие стороны равны, как у параллелограмма, и суммы их пар дают одинаковые значения, как в описанном четырёхугольнике. Значит, все стороны равны.
Теорема доказана.
