Г10. 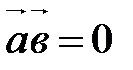

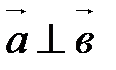 .
.
□ Пусть 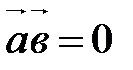 , тогда
, тогда 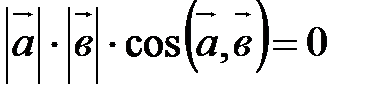
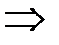
или 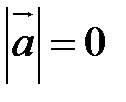
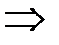
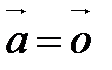
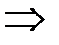
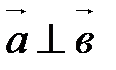 ;
;
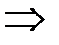 или
или 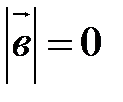
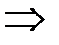
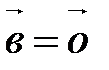
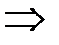
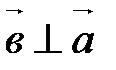
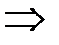
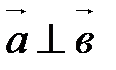 ;
;
или 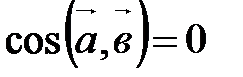
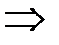
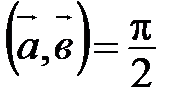
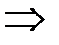
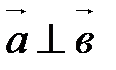 .
.
Обратно, пусть 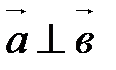 , тогда
, тогда 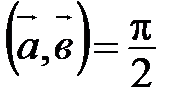
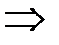
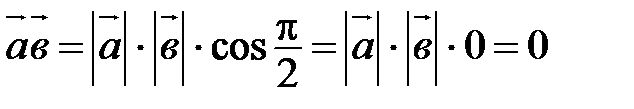 . ■
. ■
Г20. Скалярный квадрат вектора равен квадрату его длины: 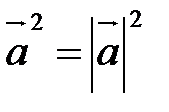 .
.
□ 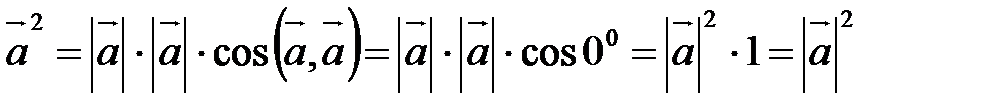 .■
.■
Из этого свойства получаем важное следствие:
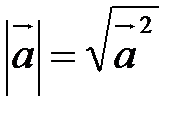 .
.
Прежде чем сформулировать третье свойство, дадим понятие проекции вектора 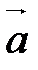 на направление, определяемое вектором
на направление, определяемое вектором 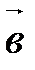 .
.
Пусть даны два вектора 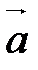 ,
, 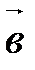 ÎV.
ÎV.
Возьмем в пространстве произвольную точку А и отложим от нее вектор 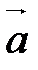 , т.е.
, т.е. 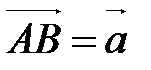 (рис. 11).
(рис. 11).
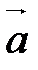 |
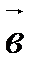 |
| А |
| В |
| А1 |
| В1 |
| s |
| Рис. 11 |
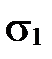 |
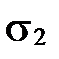 |
Возьмем прямую s|| 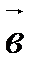 и зададим на ней направление вектором
и зададим на ней направление вектором 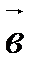 (такая направленная прямая называется осью). Проведем в пространстве через точку А плоскость
(такая направленная прямая называется осью). Проведем в пространстве через точку А плоскость 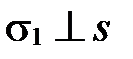 , через точку В – плоскость
, через точку В – плоскость 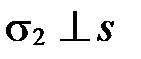 . Пусть
. Пусть 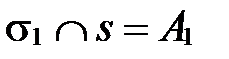 ,
, 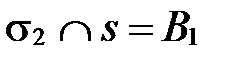 .
.
Проекцией (скалярной) вектора 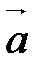 на направление, определяемое вектором
на направление, определяемое вектором 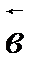 , называется число, равное
, называется число, равное
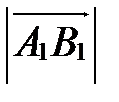 , если
, если 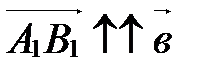 ;
;
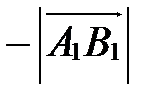 , если
, если 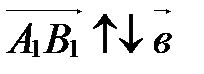 .
.
Обозначение: 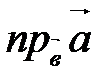 .
.
Г30. 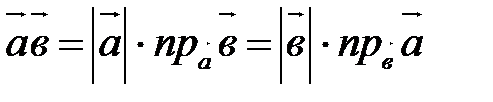 .
.
 2015-04-12
2015-04-12 1580
1580








