Центр масс системы материальных точек. Закон его движения

Пусть имеем систему материальных точек массой 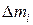. Напишем
для каждой из них второй закон Ньютона в виде:

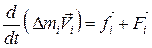, (2.2.1)

где 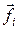— сумма всех внутренних сил, а 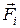— сумма внешних сил, действующих на массу 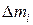. Суммируя по всем элементам i, получим:

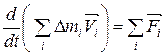, (2.2.2)

так как сумма всех внутренних сил, действующих в системе равна нулю. Следовательно, скорость изменения импульса системы материальных точек равна сумме всех внешних сил, действующих на систему.

Введем понятие центра масс системы точек. Пусть координаты элемента 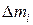в декартовой системе координат равны 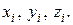Составим произведения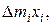 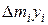, , 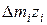просуммируем эти произведения по всем i и разделим каждую сумму на величину 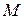, представляющую массу всей системы 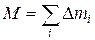. В результате получим величины:

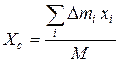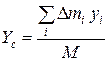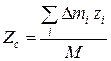, , , (2.2.3)

которые носят название координат центра масс твердого тела. Выражения (3.2.3) представим в виде:

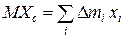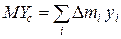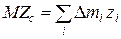, , . (2.2.4)

Дифференцируя (2.2.4) по времени, имеем:

,

,

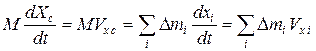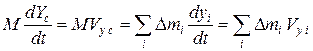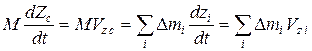(2.2.5)

или в векторной форме:

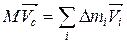. (3.2.6)

Как видно из (2.2.6), система материальных точек обладает таким же импульсом, каким обладала бы материальная точка с массой, равной суммарной массе 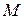и движущаяся со скоростью 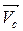, равной скорости движения центра масс системы точек. Подставляя (2.2.6) в (2.2.2), получим:

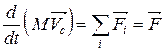. (2.2.7)

Уравнение (2.2.7) утверждает, что центр масс системы движется под действием всех внешних сил, точно так же, как двигалась бы материальная точка с массой, равной массе 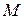, под действием тех же сил.