Метрические задачи. Определение расстояния

МЕЖДУ ДВУМЯ ТОЧКАМИ. ВЗАИМНО

ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ,

ПРЯМАЯ И ПЛОСКОСТЬ, ПЛОСКОСТИ

Контрольные вопросы

1. Как определить на эпюре расстояние между двумя точками?

2. В каких случаях прямой угол проецируется на плоскость проекций без искажения?

3. Как построить на эпюре две взаимно перпендикулярные прямые, из которых одна – общего положения, другая – линия уровня?

4. Как построить на эпюре прямую, перпендикулярную плоскости общего положения?

5. Как построить на эпюре плоскость, перпендикулярную заданной?

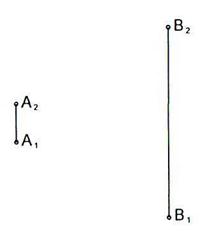
6.1 Определить расстояние между двумя точками А и В способом прямоугольного треугольника.

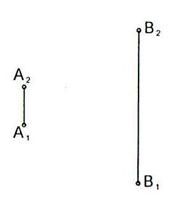
6.2 Построить горизонтальную проекцию отрезка прямой АВ длиной 45 мм.

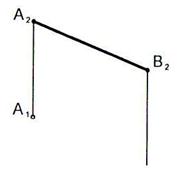
6.3 На прямой l от точки А отложить отрезок АВ длиной 30 мм.

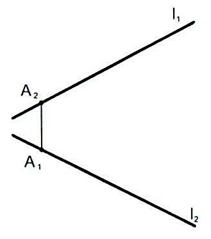
6.4 Из точки К опустить перпендикуляр на прямую CD и определить его величину.

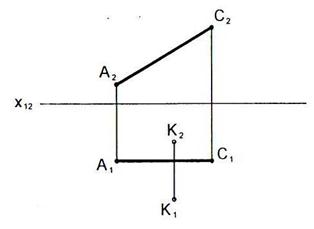
6.5 Построить равнобедренный треугольник АВС с вершиной в точке В и основанием АС, равным 40 мм, на горизонтальной прямой h.

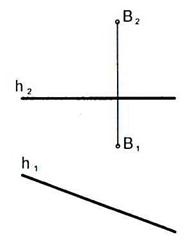
6.6 Построить ром ABCD по заданным: вершине A, направлению диагонали 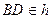и отношению диагоналей AC:BD = 1,5.

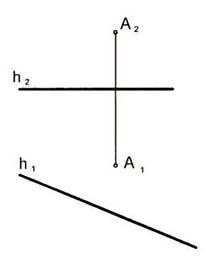
6.7 Построить квадрат ABCD по заданным: вершине A и направлению f стороны ВС.

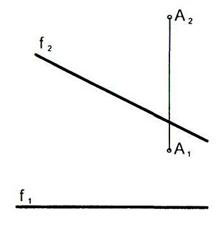
6.8 Построить горизонтальную проекцию прямоугольника ABCD.

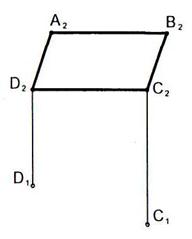
6.9 Построить прямоугольник ABCD, сторона АВ которого равна 25 мм и лежит на прямой l, сторона AD – в полтора раза больше АВ и параллельна горизонтальной плоскости проекций.

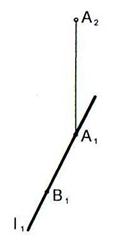
6.10 Построить точку В, симметричную точке А относительно плоскости 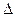, заданной параллельными прямыми l и n.

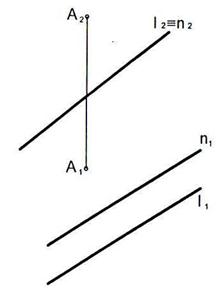
6.11 Построить геометрическое место точек, равноудаленных от точек А и В.

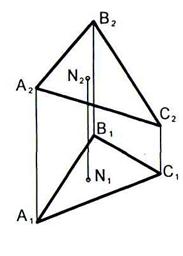
6.12 Точка N принадлежит плоскости 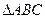. Восстановить перпендикуляр к этой плоскости длиной 20 мм.

6.13 Через точку А построить плоскость m.

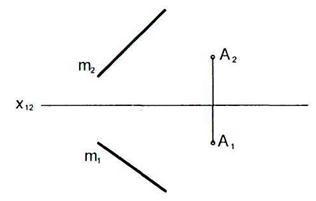
6.14 Через прямую m построить плоскость .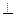

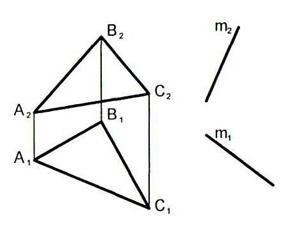
6.15 Построить плоскость 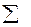, проходящую через прямую m и перпендикулярную плоскость Р.

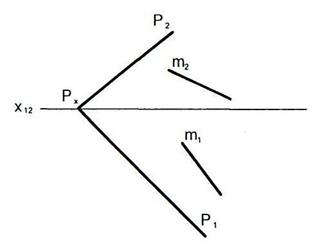
6.16 Дана плоскость 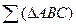. Провести плоскость 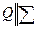, отстоящую от плоскости 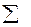на расстоянии 30 мм.

Т е м а 7