Однородной называется среда, свойства которой не зависят от координат

Как правило, типичные среды распространения электромагнитных волн являются линейными и изотропными. Однородные среды встречаются значительно реже.

Нашей ближайшей задачей является получение и решение двух уравнений, каждое из которых будет содержать только один неизвестный вектор напряженности поля, электрического Е или магнитного Н.

Начнем с уравнения, описывающего вектор напряженности магнитного поля. Для его вывода возьмем первое уравнение Максвелла (2.1) и с помощью материального уравнения (2.5) заменим в нем вектор электрической индукции произведением абсолютной диэлектрической проницаемости и вектора напряженности электрического поля. Получим:

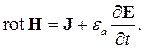(2.8)

Далее применим к этому уравнению оператор rot и изменим порядок дифференцирования по времени и координатам. Получим:

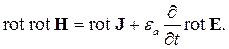(2.9)

Левую часть уравнения (2.9) надо преобразовать с помощью известно­го тождества векторного анализа, которое применительно к нашей задаче примет вид:

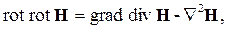(2.10)

где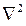

- оператор Лапласа.

Оператор div, стоящий в правой части равенства (2.10), характеризует наличие источников поля в интересующей нас точке пространства. Так как силовые линии магнитного поля непрерывны, источников они не имеют и дивергенция вектора напряженности магнитного поля всегда равна нулю: div H = 0. С учетом этого равенство (2.10) примет вид:

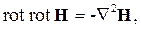(2.11)

Подставим это равенство в уравнение (2.9). Получим:

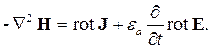(2.12)

Далее надо обратиться ко второму уравнению Максвелла (2.2) и с помощью материального уравнения (2.6) заменить в нем вектор магнитной индукции вектором напряженности магнитного поля. Получим:

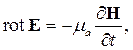(2.13)

Это соотношение позволяет исключить вектор напряженности электрического поля из уравнения (2.12). Получим:

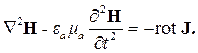(2.14)

Цель достигнута. Мы вывели уравнение, в которое входит только неизвестный вектор напряженности магнитного поля. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе они имеют вид:

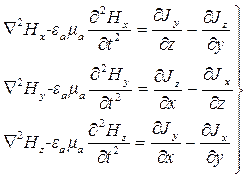(2.15)

Уравнение (2.14) можно аналогичным образом расписать в цилиндрической и в сферической системах координат. При необходимости соответствующие формулы можно найти в литературе или вывести самостоятельно.

Уравнения такого вида описывают волновые процессы и называются неоднородными уравнения­ми Даламбера, или неоднородными волновыми уравнениями.

Однако классическое волновое уравнение выглядит несколько иначе. Например, в декартовой системе координат оно имеет вид:

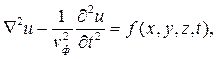(2.16)

где

vф

- фазовая скорость, м/с.

Сравнение уравнений (2.15) и (2.16) позволяет утверждать, что множитель, стоящий перед производной от составляющей вектора напряженности магнитного поля по времени также обратно пропорционален квадрату фазовой скорости:

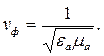(2.17)

где

vф

- фазовая скорость электромагнитной волны, м/с.

Теперь необходимо вспомнить, что абсолютная диэлектрическая проницаемость может быть представлена в виде произведения относительной диэлектрической проницаемости и электрической постоянной: ε_а = εε₀. Аналогично можно представить и абсолютную магнитную проницаемость μ_а: μ_а = μμ₀. С учетом этого формулу (2.17) можно переписать в более удобном виде:

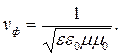(2.18)

Электрическая и магнитная постоянные – это числа. Разберемся, что получится в результате деления единицы на корень квадратный из их произведения:

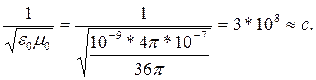(2.19)

где

с

- скорость света в вакууме, с ≈ 3*108 м/с.

Следовательно, фазовую скорость электромагнитной волны в среде можно описать формулой:

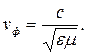(2.20)

Формула (2.20) показывает, что любое отличие характеристик среды от вакуума приводит к уменьшению фазовой скорости электромагнитных волн.

Таким образом, уравнение (2.14) примет вид:

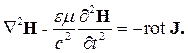(2.21)

Уравнение (2.21) получено из системы уравнений Максвелла и позволяет рассчитать напряженность магнитного поля. Подобное уравнение можно вывести и для вектора напряженности электрического поля. Надо взять второе уравнение Максвелла (2.2), применить к нему оператор rot и проделать преобразования, аналогичные выполненным выше. Получим:

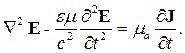(2.22)

Если правая часть уравнений (2.21) и (2.22) будет равна нулю, получатся однородные уравнения Даламбера или однородные волно­вые уравнения.

В правых частях уравнений (2.21) и (2.22) стоят все токи, протекающие в интересующем нас объеме, за исключением токов смещения. Токи смещения учтены вторым слагаемым в левой части уравнения (2.22): их величина пропорциональна скорости изменения электрического поля. Следовательно, ток J включает в себя ток проводимости J_пр и сторонний ток J_ст, если они имеются в исследуемой области пространства. Учтем этот факт в уравнениях (2.21) и (2.22). Получим:

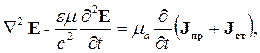	(2.23)
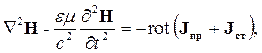	(2.24)

где	Jпр	- вектор плотности тока проводимости, А/м2.
	Jст	- вектор плотности стороннего тока, А/м2.

Сторонний ток J_ст обычно полагается известным, а ток проводимости J_пр создается рассчитываемым полем. Поэтому правые части уравнений надо преобразовать так, чтобы там остался только сторонний ток. Для этого надо:

· используя материальное уравнение (2.7), представить вектор плотности токов проводимости J_пр как произведение электропроводности σ на вектор напряженности электрического поля Е: J_пр = σ Е;

· подставить это выражение в уравнения (2.23) и (2.24);

· перенести произведение σ(д Е/ д t) в левую часть уравнения (2.23);

· rot E в правой части уравнения (2.24) заменить с помощью уравнения (2.13) и произведение μ_аσ(д Н/ д t) перенести в левую часть.

Получим:

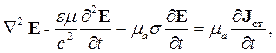	(2.25)
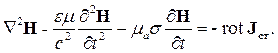	(2.26)

В левых частях уравнений (2.25) и (2.26) находятся векторы Е и Н искомого поля, а в правых – векторы плотности сторонних токов, это поле создающих. Это – наиболее общий вид волновых уравнений электродинамики.

Для описания монохроматического поля необходимо преобразовать уравнения (2.25) и (2.26) с учетом следующих особенностей метода комплексных амплитуд:

· векторы Е, Н и J_ст заменить их комплексными аналогами;

· первая производная любого вектора по времени для комплексного аналога эквивалентна умножению его jω;

· вторая производная любого вектора по времени эквивалентна умножению его –ω²;

· электрические потери, представленные в уравнениях (2.25) и (2.26) электропроводностью σ, учитываются введением комплексной абсолютной диэлектрической проницаемости:

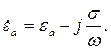(2.27)

· магнитными потерями пренебрегаем.

В результате этих преобразований получим:

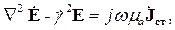	(2.28)
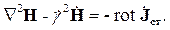	(2.29)

где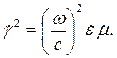

- комплексное волновое число.

Уравнения такого вида называют неоднородными уравнениями Гельмгольца или неоднородными волновыми уравнениями для комплексных амплитуд.

Если в интересующей нас области пространства сто­ронние источники отсутствуют, то есть J_cт = 0, то уравнения (2.28) и (2.29) уп­рощаются:

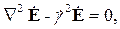	(2.30)
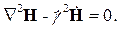	(2.31)

Такие уравнения называются однородными урав­нениями Гельмгольца или однородными волновыми уравнениями для комплексных амплитуд.

Их и необходимо решать для того, чтобы описать монохроматическую электромагнитную волну в области без источников.