Так как процесс создания электромагнитных волн нас пока не интересует, рассмотрим гармонические колебания в области, не содержащей источников. Для его описания необходимо решить уравнения (2.30) и (2.31). В такой записи вид уравнений не зависит от системы координат, в которой их необходимо решать. От системы координат зависит только оператора Лапласа.
Найдем простейшее решение волновых уравнений в декартовой системе координат и выясним их физическое содержание. Для этого проанализируем параметры электромагнитной волны от точечного источника, находящегося в точке 0 (рис. 3.1). Через источник и исследуемую область проведена ось z. Распространение электромагнитной волны вдоль этой оси мы и должны описать.
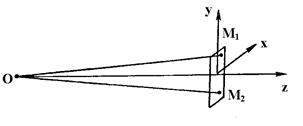 |
| Рис. 3.1. Решение волновых уравнений в декартовой системе координат |
Для этого рассмотрим площадку, перпендикулярную оси z. Будем полагать, что площадка расположена очень далеко от источника, так далеко, что любые две ее точки можно считать находящимися на одинаковых расстояниях. Пусть это будут точки М1 и М2 на рис. Рассмотрим отрезки 0М1 и 0М2, соединяющие выбранные точки площадки с источником. В пределах принятого допущения они равны и параллельны. Это значит, что точки М1 и М2 по отношению к источнику совершенно равноправны. Следовательно, при переходе от точки М1 к точке М2 мы не заметим изменений характеристик электромагнитного поля.
Характеристики волны на площадке не зависят от поперечных координат х и у, значит, частные производные векторов поля по этим координатам равны нулю. Отсюда вытекает упрощение оператора Лапласа. В его составе останется только вторая производная по продольной координате z:
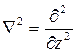 | (3.1) |
Естественно, упрощаются и волновые уравнения. Так, уравнение (2.31) примет вид:
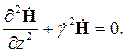 | (3.2) |
Это уравнение выбрано для примера: уравнение (2.30) решается точно так же и для понимания способа описания характеристик поля достаточно решить любое из однородных волновых уравнений для комплексных амплитуд.
Решение уравнения (3.2) известно. Дело в том, что математические формулировки большинства задач электродинамики не являются уникальными. Макроскопическая электродинамика сложилась только во второй половине 19 века. К тому времени уже было сформулировано и решено значительное количество волновых задач из других областей науки, в частотности, из механики. Поэтому при решении задач электродинамики часто достаточно преобразовать уравнение к виду, решение которого уже известно.
К этому же классу задач относится и дифференциальное уравнение (3.2). Его общее решение описывается формулой:
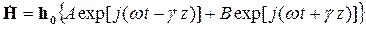 | (3.3) |
| где | h0 | - орт, указывающий ориентацию вектора напряженности магнитного поля в пространстве; |
| А, В | - произвольные коэффициенты, имеющие размерность напряженности магнитного поля, А/м; |
Входящее в них комплексное волновое число используется для описания изменения амплитуды и фазы волны при распространении. Оно состоит из действительной и мнимой части:
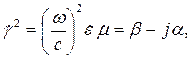 | (3.4) |
| где | β | - коэффициент фазы, рад/м; |
| α | - коэффициент затухания, 1/м. |
Изменение фазы при распространении описывает произведение βz, а амплитуда убывает по экспоненциальному закону: exp(-αz) Действительное волновое число соответствует среде без потерь и равно коэффициенту фазы.
Формула (3.3) описывает электромагнитную волну, распространяющуюся вдоль оси z. При постановке задачи мы потребовали, чтобы на плоскости, перпендикулярной оси z, характеристики поля не зависели от поперечных координат х и у. А что такое характеристики поля в данном случае? Это амплитуда напряженности поля и фаза волны. Значит, фаза волны постоянна на плоскости и волна является плоской. В математическом описании волны о том, что она плоская, говорит зависимость фазы, то есть показателя степени экспонент, от единственной координаты z.
Кроме фазы, на плоскости фронта не изменяется и амплитуда напряженности поля. Это ее свойство мы также оговорили в условии задачи. Следовательно, волна, является однородной.
В формулу (3.3) расстояние входит только в мнимый показатель степени экспоненты. Это означает, что при распространении в среде без потерь с расстоянием изменяется только фаза волны, а амплитуда постоянна.
 2015-04-01
2015-04-01 1257
1257
