Лабораторная работа № 4

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ РАЗОМКНУТЫХ И ЗАМКНУТЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Цель. Рассмотреть структурную схему (рис. 4.1).

1. Для звена, с передаточной функцией W₃(p), выбираемого из табл. 4.1 приложения в соответствии с вариантом заданным преподавателем, построить переходной процесс и сделать заключения об устойчивости объекта. Сделать заключение об устойчивости объекта по коэффициентам и корням характеристического уравнения. Построить годограф Михайлова и сделать заключение об устойчивости объекта по критерию Михайлова. Построить амплитудно-фазовую характеристику объекта без обратной связи и по критерию Найквиста оценить устойчивость замкнутой системы, определить запас устойчивости по амплитуде и фазе.

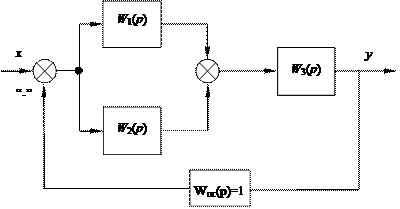
Рис. 4.1. Структурная схема системы с параллельным соединением звеньев W ₁(p) и W ₂(p) и последовательным присоединением к ним звена W ₃(p)

2. Провести анализ устойчивости разомкнутой и замкнутой систем (см. рис. 4.1), содержащих в прямой цепи, подключенные параллельно два звена, с передаточными функциями W₁(p) и W₂(p) соответственно, и последовательно соединенное с ними звено, с передаточной функцией W₃(p), выбираемых из табл. 4.1 приложения, в соответствии с вариантом. Проанализировать влияние соотношения коэффициентов звеньев на устойчивость системы.

Теоретическая часть

Понятие устойчивости является важнейшей качественной оценкой динамических свойств САР. Под устойчивостью понимают способность системы восстанавливать исходное состояние равновесия после снятия внешнего возмущения.

Рис. 4.2. К понятию устойчивость систем: t ₁ – время внесения возмущения;

x _в(t) – вынужденное движение системы; x _с(t) – свободное движение системы

Различают три типа систем:

1) устойчивые системы – это системы, которые, будучи выведены из состояния равновесия каким-либо внешним возмущением, после снятия этого возмущения возвращаются в исходное состояние равновесия;

2) нейтральные системы – системы, которые после снятия возмущения приходят в состояние равновесия, отличное от исходного;

3) неустойчивые системы – такие системы, в которых не устанавливается равновесия после снятия возмущения.

Пусть система находилась в равновесии (см. рис. 4.2). В момент времени t ₁ под действием внешнего возмущения система была выведена из этого состояния. Движение системы под действием возмущения называют вынужденным (x _в(t)). Затем, в некоторый момент времени t = 0 (принятое за начало отсчета), возмущение было снято или скомпенсировано. Начинается свободное движение системы (x _c(t)). Переходный процесс h (t) = x _в(t) + x _c(t). Причем, если 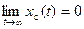– система устойчивая, 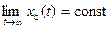– система нейтральная, 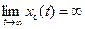– система неустойчивая.

С целью упрощения анализа устойчивости систем разработан ряд специальных методов, которые получили название критериев устойчивости. Критерии устойчивости делятся на две разновидности: алгебраические и частотные. Алгебраические критерии являются аналитическими, а частотные – графоаналитическими. Но все они базируются на критерии Ляпунова.

Критерий Ляпунова

Формулировка критерия. Необходимым и достаточным условием устойчивости линейной системы является условие, когда все вещественные корни характеристического уравнения системы, а также действительные части комплексных корней, отрицательны. Если хотя бы один из корней положителен – система неустойчива; если равен 0 – система находится на границе устойчивости (рис. 4.3). Мнимая ось Im является границей устойчивости.

Однако пользоваться этим условием на практике для оценки устойчивости реальных систем оказывается достаточно сложно. Это связано с тем, что реальные промышленные системы описываются дифференциальными уравнениями высокого порядка или содержат звенья чистого запаздывания, так что нахождение корней характеристического уравнения представляет трудную задачу.

Для таких систем применяются следующие критерии устойчивости: алгебраический критерий Рауса-Гурвица; частотный критерий Михайлова; амплитудно-фазочастотный критерий Найквиста.

Алгебраический критерий устойчивости (Критерий Рауса-Гурвица)

Критерий Рауса-Гурвица является наиболее распространенным алгебраическим критерием и применяется для определения устойчивости системы, когда известно характеристическое уравнение. Характеристическое уравнение – знаменатель передаточной функции.

Формулировка критерия. Необходимым условием устойчивости линейной системы является условие – все коэффициенты характеристического уравнения положительны; достаточным условием устойчивости линейной системы является условие – все определители, составленные из коэффициентов характеристического уравнения, положительны. Если хотя бы один из определителей равен 0 – система находится на границе устойчивости. Если какой-либо из определителей меньше 0 – система не устойчива.

Пусть характеристическое уравнение системы имеет вид:

.

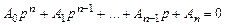Необходимое условие устойчивости: A ₀ > 0, A ₁ > 0, …, A _n-1 > 0, A _n > 0. Достаточное условие устойчивости:

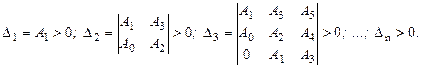
Правило составления определителей. В главную диагональ определителя n -го порядка записываются все коэффициенты, начиная с первого. Столбцы матрицы вверх от главной диагонали заполняются коэффициентами с порядковыми номерами по возрастанию индексов, вниз – по убыванию индексов. Все элементы определителя, индексы которых больше порядка характеристического уравнения и меньше 0, заполняют нулями.

Пример. Исследовать устойчивость системы, характеристическое уравнение которого имеет вид: 3 p ⁴ + 4 p ³ + 4 p ² + 2 p + 1 = 0.

Необходимое условие устойчивости: A ₀= 3 >0, A ₁= 4 >0, A ₂= 4 >0, A ₃= 2 >0, A ₄= 1 >0.

Достаточное условие устойчивости:

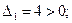
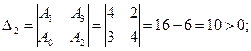
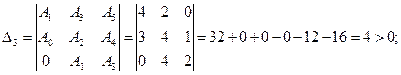
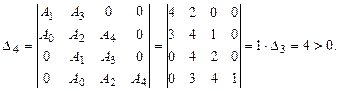
Вывод: все условия выполнены, система устойчива.

Частотный критерий Михайлова

Так же как и алгебраический критерий, частотный критерий применяется в тех случаях, когда задано характеристическое уравнение системы:

.

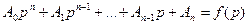Обозначим полином, стоящий в левой части характеристического уравнения, через D (p), т.е. .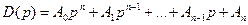

Заменим p на jw. Получим вектор характеристического полинома:

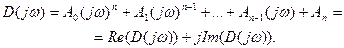
При изменении w от 0 до ¥ вектор D (jw) опишет кривую, называемую годограф Михайлова.

Формулировка критерия. Система будет устойчива в том случае, если годограф Михайлова при изменении частоты от 0 до ¥ начинается на положительной части действительной оси комплексной плоскости, проходит последовательно против часовой стрелки n квадрантов плоскости, нигде не обращается в 0 и не проходит через начало координат (n – порядок характеристического уравнения системы). Если годограф проходит через начало координат комплексной плоскости, то система находится на границе устойчивости, если нарушается хотя бы одно из условий критерия – система неустойчива.

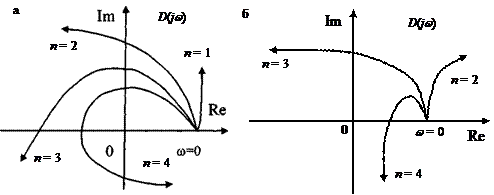На рис. 4.4 приведены примеры годографов Михайлова D (jw).

Рис. 4.4. Годограф Михайлова: а - системы устойчивые;

б - системы неустойчивые

Пример. Определить устойчивость системы, характеристический полином которой имеет вид: D (p) = 2 p ³ + 9 p ² + 13 p + 6.

Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:

D (jw) = 2(jw)³ + 9(jw)² + 13(jw) + 6 = –2 jw ³ – 9 w ² + 13 jw + 6 =

= (6 – 9 w ²) + j (13 w – 2 w ³).

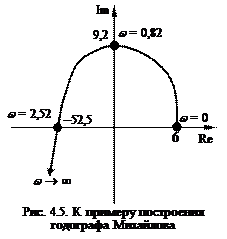Выделяем действительную и мнимую части: Re (w) = 6 – 9 w ²; Im (w) =13 w – 2 w ³.

Задаваясь значениями частоты из интервала [0; ¥), строим годограф Михайлова (рис. 4.5):

1) w = 0, Re = 6, Im = 0 – годограф начинается на положительной части действительной оси Re;

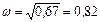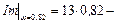
2) Re = 0 Þ 6 – 9 w ² =0Þ ; 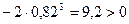– годограф начинает поворачиваться против часовой стрелки и пересекает мнимую ось Im;

3) Im = 0 Þ 13 w – 2 w ³ = 0; w (13–2 w ²) = 0; w ₁ = 0; 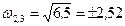; при w =2,52 Re =6–9×2,52²=–52,2<0 – годограф продолжает поворачивается против часовой стрелки, пересекает действительную ось Re, проходит 3 квадранта и при w ® ¥ остается в третьем квадранте, что соответствует порядку характеристического полинома, т.е. w ® ¥, Re ® – ¥, Im ® ¥.

Вывод. Все условия критерия Михайлова соблюдены, система устойчива.

Амплитудно-фазовый критерий Найквиста

Амплитудно-фазовый критерий Найквиста служит для определения устойчивости замкнутой системы, охваченной отрицательной статической обратной связью, по АФЧХ разомкнутой системы (рис. 4.6).

Статическая отрицательная обратная связь имеет передаточную функцию W _ос = – 1.

Формулировка критерия. Замкнутая система будет устойчива, если разомкнутая система устойчива, и ее амплитудно-фазо-частотная характеристика не охватывает на комплексной плоскости точку с координатами (–1; j 0). Если АФЧХ проходит через точку (–1; j 0), то система находится на границе устойчивости, если охватывает – то система неустойчивая (рис. 4.7).

У астатических разомкнутых систем, которые содержат интегрирующие звенья, амплитудно-фазо-частотные характеристики не образуют замкнутого контура. При частоте w = 0 частотная передаточная функция астатической системы обращается в ¥, а ее амплитудо-фазо-частотная характеристика претерпевает разрыв. Поэтому в этом случае трудно решить вопрос об устойчивости замкнутой системы, так как неясно, охватывает ли амплитудно-фазо-частотная характеристика W (jw) точку (–1; j 0).

Для определения устойчивости систем с астатизмом любого порядка n достаточно построить одну ветвь амплитудно-фазо-частотной характеристики разомкнутой системы, соответствующую положительным частотам. Дополнить ее дугой 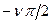окружности бесконечно большого радиуса, такого, чтобы АФЧХ получилась замкнутой на действительную ось. Затем применить критерий устойчивости Найквиста.

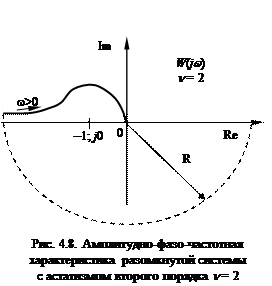На рис. 4.8. приведена амплитудно-фазо-частотная характеристика разомкнутой системы с астатизмом второго порядка n = 2. Замкнутая система в этом случае будет неустойчива, так как амплитудно-фазо-частотная характеристика W (jw), дополненная дугой 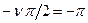бесконечно большого радиуса, всегда охватывает точку (–1; j 0) в отрицательном направлении (по часовой стрелке).

Удаление АФЧХ разомкнутой системы W (jw) от точки (–1; j 0) определяет запас устойчивости, который характеризуется двумя величинами: запасом устойчивости по фазе и запасом устойчивости по амплитуде.

Запас устойчивости по фазе определяют как величину угла j = p – (y (w _с)) для частоты w _с, при которой ½ W (w _с)½ = 1; запас устойчивости по амплитуде определяется как величину отрезка оси абсцисс h, заключенного между критической точкой (–1; j 0) и АФЧХ (рис. 4.9).

Правила записи передаточной функции системы, состоящей из нескольких звеньев, соединенных различными способами см. теоретический материал к выполнению лабораторной работы № 2.