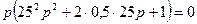1. Для звена W 3(p) (см. рис. 4.1) построить переходной процесс при единичном ступенчатом воздействии, по которому определить его устойчивость.
2. Провести оценку устойчивости объекта по алгебраическим критериям: корневому и Рауса-Гурвица.
3. Провести оценку устойчивости объекта по частотному критерию Михайлова. Построить амплитудно-фазовую характеристику объекта без обратной связи и по критерию Найквиста оценить устойчивость замкнутой системы. Если рассматриваемое звено устойчиво, определить запас устойчивости по амплитуде и фазе.
4. Аналогичным образом проанализировать устойчивость разомкнутой системы, состоящей из трех звеньев (см. рис. 4.1).
5. Аналогичным образом проанализировать устойчивость замкнутой системы, а также провести оценку устойчивости замкнутой системы по критерию Найквиста.
6. проанализировать влияние соотношения коэффициентов звеньев на устойчивость замкнутой системы, используя один из критериев.
Примеры расчета
Пример 1. Для звена заданного передаточной функцией:
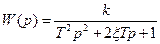 ,
,
1) построить переходной процесс, сделать заключения об устойчивости объекта;
2) сделать заключение об устойчивости объекта по коэффициентам и корням характеристического уравнения;
3) построить годограф Михайлова, сделать заключение об устойчивости объекта по критерию Михайлова;
4) построить амплитудно-фазовую характеристику объекта без обратной связи и по критерию Найквиста оценить устойчивость замкнутой системы, определить запас устойчивости по амплитуде и фазе.
Решение
1. Передаточная функция колебательного звена:
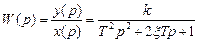 , откуда
, откуда 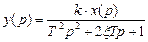 .
.
Передаточная функция для единичного ступенчатого воздействия 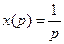 имеет вид:
имеет вид: 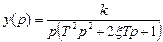 .
.
Выполним обратное преобразование Лапласа (см. приложение, табл. 3) и получим переходной процесс для единичного ступенчатого воздействия:
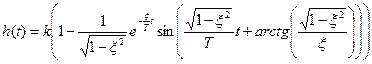 .
.
Строим график переходного процесса при T =25, x = 0,5, k = 8 (рис. 4.10)
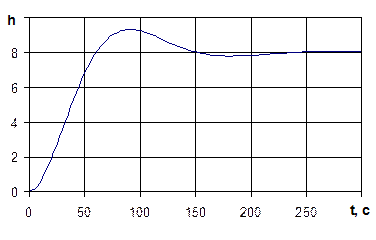
Рис. 4.10. Переходной процесс колебательного звена при T =25, x = 0,5, k = 8
Из графика следует, что объект нейтрален.
2. Оценка устойчивости по алгебраическим критериям:
Корневой критерий
Характеристическое уравнение для передаточной функции колебательного звена: 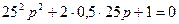
имеет 2 комплексных корня: 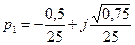 ,
, 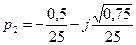 . Действительные части комплексных корней, отрицательны, следовательно объект является устойчивым.
. Действительные части комплексных корней, отрицательны, следовательно объект является устойчивым.
Критерий Рауса-Гурвица
Так как все коэффициенты характеристического уравнения положительны, то необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения:
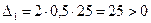 ,
, 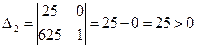 .
.
Так как все определители, составленные из коэффициентов характеристического уравнения, положительны, объект является устойчивым.
3. Оценка устойчивости по частотным критериям
Критерий Михайлова
В характеристическом полиноме 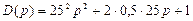 . Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
. Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
D (jw) = 625(jw)2 + 25(jw) + 1 = – 625 w 2 + 25 jw + 1 =
= (1 – 625 w 2) + j× 25 w.
Выделяем действительную и мнимую части: Re = 1 – 625 w 2; Im = 25 w. Задаваясь значениями частоты из интервала [0; ¥[, строим годограф Михайлова (рис. 4.11).
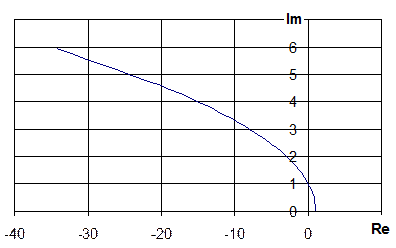
Рис. 4.11. Годограф Михайлова для 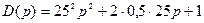
Вывод. Годограф Михайлова при изменении частоты от 0 до ¥ начинается на положительной части действительной оси комплексной плоскости при w = 0 Re = 1, Im = 0, проходит последовательно против часовой стрелки n квандрантов плоскости, нигде не обращается в 0 и не проходит через начало координат (n = 2 – порядок характеристического уравнения системы). Следовательно объект устойчив.
Критерий Найквиста
Для разомкнутой системы 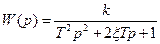 . Заменяем р на jw, освобождаемся от иррациональности в знаменателе и группируем слагаемые, содержащие и не содержащие j:
. Заменяем р на jw, освобождаемся от иррациональности в знаменателе и группируем слагаемые, содержащие и не содержащие j:
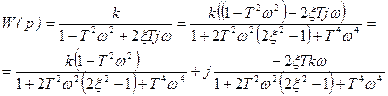 , откуда
, откуда
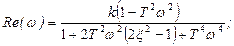
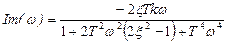 .
.
Задаваясь значениями частоты из интервала [0; ¥[, строим АФЧХ колебательного звена (рис. 4.12).
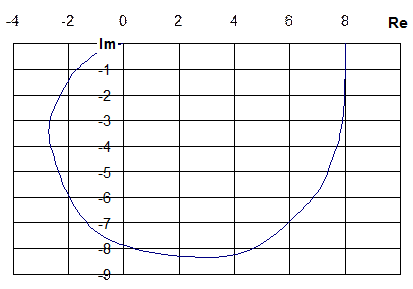
Рис. 4.12. Амплитудно-фазо-частотный критерий Найквиста для 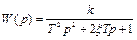
Вывод. Разомкнутая система устойчива, а так как амплитудно-фазо-частотная характеристика разомкнутой системы не охватывает на комплексной плоскости точку с координатами (–1; j 0), следовательно замкнутая система будет тоже устойчива.
Запас устойчивости по фазе: 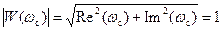 при w с = 0,116. Тогда
при w с = 0,116. Тогда 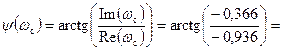
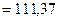 град., j = p – (y (w с)) = = 180 – 111,37 = 68,63 град.; запас по амплитуде: h =1 – отрезок, заключенный между критической точкой (–1; j 0) и АФЧХ при пересечении ею оси абсцисс.
град., j = p – (y (w с)) = = 180 – 111,37 = 68,63 град.; запас по амплитуде: h =1 – отрезок, заключенный между критической точкой (–1; j 0) и АФЧХ при пересечении ею оси абсцисс.
Пример 2. Провести анализ устойчивости разомкнутой и замкнутой систем, содержащих в прямой цепи, подключенные параллельно два звена, с передаточными функциями 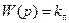 и
и 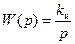 , где kп= 1; kи= 0,5 и последовательно соединенное с ними звено с передаточной функцией
, где kп= 1; kи= 0,5 и последовательно соединенное с ними звено с передаточной функцией 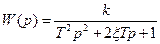 , где T = 25, x = 0,5, k = 8 (см. рис. 4.1). Проанализировать влияние соотношения коэффициентов звеньев на устойчивость системы.
, где T = 25, x = 0,5, k = 8 (см. рис. 4.1). Проанализировать влияние соотношения коэффициентов звеньев на устойчивость системы.
Решение
1. Передаточная функция разомкнутой системы:
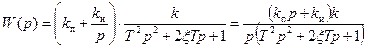 .
.
2. Алгебраические критерии.
Корневой критерий
имеет 2 комплексных корня: 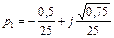 ,
, 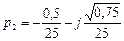 и один нулевой корень p 3 = 0. Действительные части комплексных корней, отрицательны, следовательно разомкнутая система находится на границе устойчивости.
и один нулевой корень p 3 = 0. Действительные части комплексных корней, отрицательны, следовательно разомкнутая система находится на границе устойчивости.
Критерий Рауса-Гурвица
Так как все коэффициенты характеристического уравнения положительны, то необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения 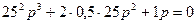 .
.
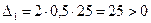 ,
, 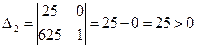 ,
,
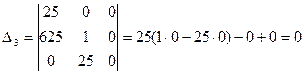 .
.
Так как один определитель (D3), составленный из коэффициентов характеристического уравнения, нулевой, а два положительны, разомкнутая система находится на границе устойчивости.
3. Частотные критерии
Критерий Михайлова
В характеристическом полиноме D (p)= p× (252 p 2+2×0,5×25 p +1). Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
D (jw) = (625(jw)2 + 25(jw) + 1)×(jw) = – 625 jw 3 – 25 w 2 + 1 jw =
= – 25 w 2 + j× (w – 625 w 3).
Выделяем действительную и мнимую части:
Re = – 25 w 2; Im = w – 625 w 3.
Задаваясь значениями частоты из интервала [0; ¥[, строим годограф Михайлова (рис. 4.13).
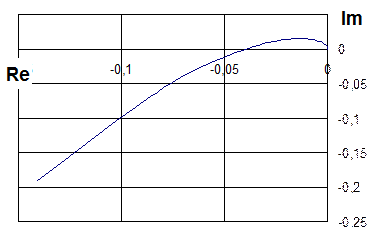
Рис. 4.13. Годограф Михайлова для 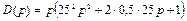
Годограф Михайлова при изменении w =[0; +¥) начинается в начале координат комплексной плоскости, проходит против часовой стрелки по квадрантам плоскости и уходит в бесконечность в третьей четверти. Следовательно разомкнутая система находится на границе устойчивости.
4. Передаточная функция замкнутой системы с отрицательной единичной обратной связью равна:
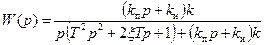 .
.
5. Алгебраические критерии
Корневой критерий
Так как характеристическое уравнение исследуемой системы
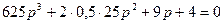 достаточно трудоемко в решении анализ устойчивости по корневому критерию проводить не будем, ограничившись критерием Рауса-Гурвица.
достаточно трудоемко в решении анализ устойчивости по корневому критерию проводить не будем, ограничившись критерием Рауса-Гурвица.
Критерий Рауса-Гурвица
Все коэффициенты характеристического уравнения положительны - необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения 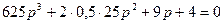 .
.
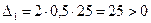 ,
,
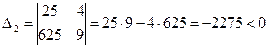 ,
,
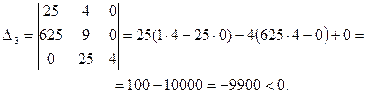
Так как один определитель (D1), составленный из коэффициентов характеристического уравнения, положителен, а два отрицательны, замкнутая система неустойчива.
6. Частотные критерии
Критерий Михайлова
В характеристическом полиноме 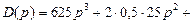
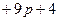 . Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
. Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
D (jw) = 625(jw)3 + 25(jw)2 + 9(jw) + 4 = – 625 jw 3 – 25 w 2 + 9 jw + 4 =
= (– 25 w 2 + 4) + j (w× (9 – 625 w 2).
Выделяем действительную и мнимую части:
Re = –25 w 2+ 4; Im = w ×(9 – 625 w 2).
 Задаваясь значениями частоты из интервала [0; ¥[, строим годограф Михайлова (рис. 4.14):
Задаваясь значениями частоты из интервала [0; ¥[, строим годограф Михайлова (рис. 4.14):
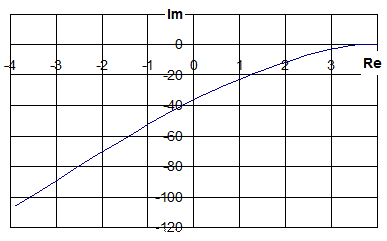
Рис.4.14. Годограф Михайлова для 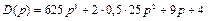
Годограф Михайлова при изменении частоты от 0 до ¥ начинается на положительной части действительной оси комплексной плоскости, не проходит последовательно против часовой стрелки 3 квадранта плоскости, обращается в 0 и уходит в бесконечность в третьей четверти.
Следовательно, замкнутая система неустойчива.
Критерий Найквиста:
По Амплитудно-фазовому критерию Найквиста устойчивости замкнутой системы, охваченной отрицательной статической обратной связью, определяется по АФЧХ разомкнутой системы. Для разомкнутой системы 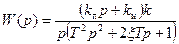 . Заменяем р на jw, освобождаемся от иррациональности в знаменателе и группируем слагаемые, содержащие и не содержащие j:
. Заменяем р на jw, освобождаемся от иррациональности в знаменателе и группируем слагаемые, содержащие и не содержащие j:
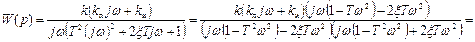
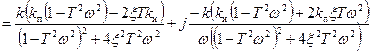 , откуда
, откуда
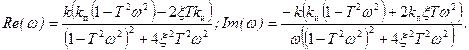
Задаваясь значениями частоты из интервала [0; ¥[, строим АФЧХ разомкнутой системы, а, поскольку, система содержит интегрирующее звено, то есть АФЧХ имеет разрыв, дополняем годограф дугой – p /2, начинающейся на положительной полуоси и проходящей по часовой стрелке до пересечения с годографом (пунктирная линия на рис. 4.15):
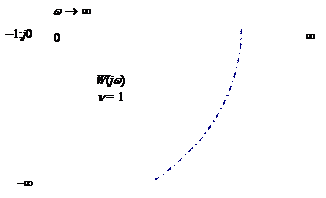
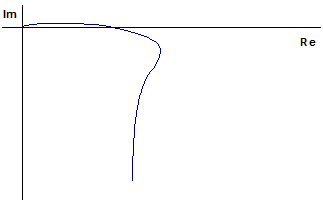
Рис. 4.15. Годограф разомкнутой системы для анализа устойчивости
по критерию Найквиста
Так как разомкнутая система находится на границе устойчивости (см. выше) и ее годограф не охватывает точку (–1; j 0), то замкнутая система является неустойчивой.
7. Проанализируем влияние соотношения коэффициентов звеньев на устойчивость замкнутой системы, используя критерий Михайлова.
Характеристический полином 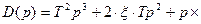
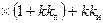 . Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
. Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j:
D (jw) = T 2(jw)3 + 2× xT (jw)2 + (jw)×(1+ kk п) + kk и = – T 2 jw 3 – 2× xT w 2 +
+ (jw)×(1+ kk п) + kk и = (–2× xT w 2 + kk и) + j (w× ((1+ kk п) – T 2 w 2).
Выделяем действительную и мнимую части: Re= (–2× xT w 2 + + kk и); Im = (w× ((1+ kk п) – T 2 w 2).
Задаваясь значениями частоты из интервала [0; ¥[, строим годографы Михайлова при изменении по отдельности каждого из коэффициентов (рис. 4.16):
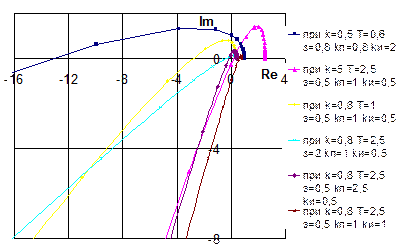
Рис. 4.16. Годограф Михайлова при различных значениях коэффициентов
При увеличении k годограф сдвигается по оси абсцисс вправо и наоборот. При уменьшении T годограф как бы раскручивается, при увеличении наоборот. При увеличении x наклон годографа к оси абсцисс уменьшается. При увеличении k п, увеличивается выпуклость годографа, при уменьшении годограф сглаживается. При увеличении k и наклон годографа к оси абсцисс увеличивается.
В результате варьирования коэффициентов звеньев получили устойчивую замкнутую систему. Подтвердим устойчивость системы методом Рауса-Гурвица. Так как все коэффициенты характеристического уравнения 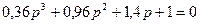 положительны, то необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения.
положительны, то необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения.
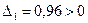 ,
, 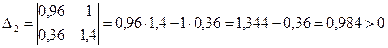 ,
,
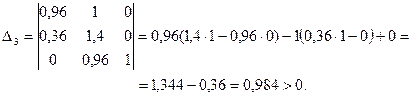
Так как все определители, составленные из коэффициентов характеристического уравнения положительны, то замкнутая система устойчива.
Контрольные вопросы
1. Понятие устойчивости САР.
2. Определение устойчивости по временным характеристикам.
3. Методы, используемые для определения устойчивости САР.
4. Критерий Ляпунова.
5. Критерий Рауса-Гурвица.
6. Критерий Михайлова.
7. Критерий Найквиста.
8. Определение устойчивости систем с астатизмом по критерию Найквиста.
9. Запас устойчивости. Определение запаса устойчивости.
ЛАБОРАТОРНАЯ РАБОТА № 5
 2015-04-12
2015-04-12 895
895