Метод логарифмирования применяется для изменения влияния факторов только в мультипликативных моделях.
Порядок факторов в методе не важен. При использовании этого метода достигается еще более высокая точность, чем при использовании интегрального метода. В этом достоинство метода, а недостаток – в ограниченности применения.
Рассмотрим трехфакторную мультипликативную модель.
y = a∙b∙c
Прологарифмируем обе части равенства по любому основанию.
lg(y) = lg(a∙b∙c)
lg(y) = lg(a)+ lg(b) + lg(c)
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, заменим их абсолютные значения на индексы:
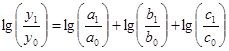
lg(Iy) = lg(Ia) + lg(Ib) + lg(Ic)
Умножим обе части равенства на 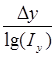 :
:
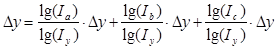
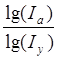 ∙∆у,
∙∆у, 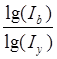 ∙∆у,
∙∆у, 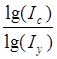 ∙∆у - частные приросты результативного показателя.
∙∆у - частные приросты результативного показателя.
Можно сделать вывод, что:
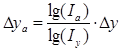
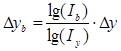
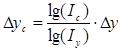
| Приемы анализа | Мультипликативная модель | Аддитивная модель | Кратная модель | Смешанная модель |
| Цепная подстановка | + | + | + | + |
| Индексный | + | - | + | - |
| Абсолютных разниц | + | - | - | y=(a-b)▪c y=a▪(b-c) |
| Относительных (процентных) разниц | + | - | - | y=(a-b)▪c |
| Пропорционального деления (долевого участия) | - | + | - | y=a/(b+c+…) |
| Интегральный | + | - | + | y=a/b+c+… |
| Логарифмирования | + | - | - | - |
 2015-04-12
2015-04-12 522
522








