Сечение цилиндра плоскостью

Цилиндр является поверхностью проецирующей. При пересечении цилиндра плоскостью, параллельной основанию (рис.126 а), в сечении получаем окружность. Плоскость, параллельная двум образующим (рис.126 6), в сечении дает прямоугольник. При пересечении цилиндра плоскостью (рис126 в) в сечении получаем эллипс.

Рис.126 а

Рис.126 б Рис.126 в

Пересечение цилиндра с фронтально-проецирующей плоскостью показано на рис. 127.

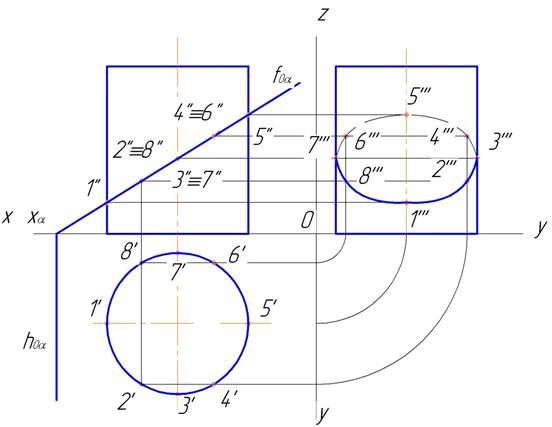
Рис.127

Пересечение прямой с поверхностью

При пересечении прямой с поверхностью нужно определить точки входа и выхода прямой из данной поверхности.

Алгоритм решения такой задачи сводится к следующему:

1.заключить прямую во вспомогательную плоскость;

2. построить линию пересечения вспомогательной плоскости с заданной поверхностью (построить фигуру сечения);

3.найти точки пересечения прямой с контуром фигуры сечения;

4.определить видимость прямой.

Пример 1. Конус (рис.128)

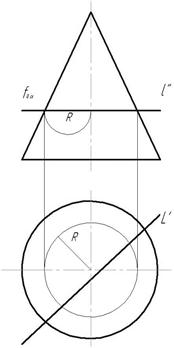
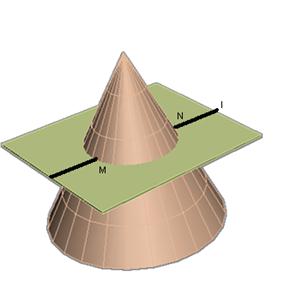
Рис.129

1. Заключаем прямую l 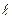в плоскость частного положения так, чтобы при пересечении конуса с плоскостью была простая линия пересечения – окружность. В данной задаче α – горизонтальная плоскость, f_оα собирающий след, l'' 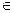f_оα (рис. 130).

2. Строим линию пересечения конуса с плоскостью α. Это окружность радиуса R.

3. На пересечении горизонтальной проекции l' и окружности радиуса R отметим искомые горизонтальные проекции M' и N'. M'' и N'' отмечаем на l''.

4. Определяем видимость прямой l. Между получившимися точками M и N прямая всегда невидима. Горизонтальная проекция прямая l' видима (невидима только от M' до N'). Фронтальная проекция l'' до М'' видима, т.к. точка М лежит на видимой части конуса относительно π₂. Точка N лежит на невидимой части конуса относительно π₂, следовательно, фронтальная проекция l'' от N'' до очерковой образующей невидима. За очертаниями конуса прямая l всегда видима (рис.130).

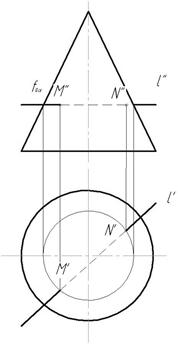Рис.130 Рис.131

Пример 2. Гранная поверхность - призма (рис.131)

1. Заключаем прямую l во вспомогательную плоскость частного положения. Линией пересечения плоскости с гранной поверхностью будет ломаная линия. Заключаем прямую l во фронтально-проецирующую плоскость α 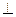π₂, l'' 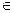f_oα, f_oα – собирающий след (рис.131).

2. Строим линию пересечения плоскости α с призмой. Отметим 1'', 2'', 3'' на собирающем следе f_oα.

3. Построим горизонтальные проекции 1', 2' и 3' на соответствующих ребрах.

4. Соединяем горизонтальные проекции 1'-2'-3' ломаной линией с учетом видимости.

5. На пересечении горизонтальной проекции l' с горизонтальной проекцией 1'-2'-3' отметим горизонтальные проекции M' и N' искомых точек М и N.

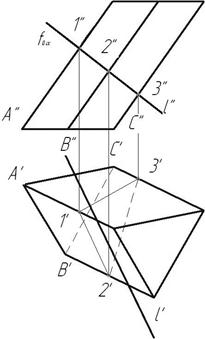Рис.132 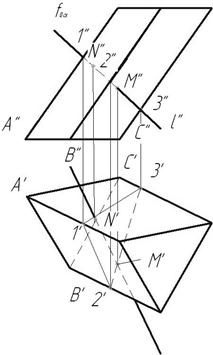Рис.133

6. Построим фронтальные проекции M'' и N'' на l''.

7. Определяем видимость прямой l. Между полученными точками M и N прямая невидима всегда. Горизонтальная проекция l' невидима между M'N' и от M' до горизонтальной проекции ребра В', т. к. горизонтальная проекция М' принадлежит невидимой относительно π₁ грани ВС. На π₂: точка М лежит на грани BС видимой относительно π₂, следовательно, М'' видима, и фронтальная проекция l" видима до М''. Точка N принадлежит грани АC, невидимой относительно π₂, следовательно, фронтальная проекция N'' не видима, и фронтальная проекция l'' от N'' невидима. За очертаниями призмы прямая l видима (рис.133).

Пример 3. Пересечение прямой со сферой показано на рис. 134. 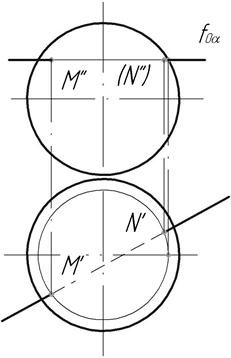Рис. 134.