Основные понятия. В начертательной геометрии кривая поверхность определяется как непрерывное множество положений перемещающейся в пространстве линии

В начертательной геометрии кривая поверхность определяется как непрерывное множество положений перемещающейся в пространстве линии, называемой образующей. Образующая может быть прямой (линейчатая поверхность) или кривой (нелинейчатая) линией. Движение образующей в пространстве может осуществляться по некоторому закону. Такая поверхность называется закономерной в отличие от незакономерной (случайной) поверхности. К числу условий перемещения в пространстве образующей линии относятся: перемещение по неподвижным линиям – направляющим, вращательное движение вокруг неподвижной оси, винтовое перемещение и др.

Одна и та же поверхность может быть образована перемещением различных линий и согласно различным условиям. Например, боковая поверхность прямого кругового цилиндра может быть рассмотрена как результат:

- перемещения окружности вдоль некоторой оси;

- вращения некоторой образующей прямой линии вокруг оси вращения;

- вращения некоторой кривой линии, все точки которой равноудалены от оси вращения.

Рассматривая совокупность прямолинейных образующих с совокупностью образующих окружностей получим каркас данной поверхности цилиндра.

Множество неподвижных линий, инцидентных данной поверхности и объединенных каким-либо общим признаком, называется её каркасом.

6.2.2. Задание поверхности вращения на чертеже.
Точки и линии на поверхности

На чертеже поверхность изображают очерком проекций поверхности или её отдельных частей.

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этой поверхности.

Точка принадлежит поверхности, если она находится на линии, принадлежащей данной поверхности. Рассмотрим чертёж конуса и точки, принадлежащие его поверхности (рис. 6.6). Фронтальная проекция конуса задана очерковыми образующими, определяющими границы поверхности, а горизонтальная – проекцией основания конуса. Каркас конуса – это совокупность образующих прямых линий, соединяющих их вершину S и основание конуса и совокупность параллелей – окружностей различного радиуса, плоскость которых перпендикулярна оси конуса.

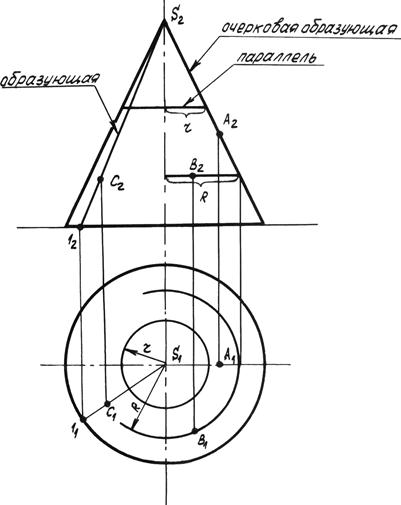
Рис. 6.6

Рассмотрим ряд точек на боковой поверхности конуса. Точка А расположена на очерковой образующей конуса, её горизонтальная проекция находится на линии связи на оси конуса. Обратим внимание, что очерковая образующая является фронталью, т. е. её фронтальная проекция – натуральная величина образующей конуса.

Принадлежность точек В и С поверхности конуса определяется соответственно с помощью параллели радиуса R или образующей конуса (S 1).

6.2.3. Позиционные задачи на пересечение поверхности
с прямой линией и плоскостью

В общем случае пересечением поверхности с плоскостью является кривая линия.

Рассмотрим конические сечения фронтально проецирующими плоскостями и горизонтальной плоскостью уровня (рис. 6.7) Обозначим угол наклона образующей к оси конуса a, а угол наклона следа плоскости – j. В зависимости от угла наклона плоскости линией сечения может быть окружность, эллипс, парабола, гипербола. Если:

j = 90°, линия сечения – окружность;

j > a – эллипс;

j = a – парабола;

j < a – гипербола.

Если секущая плоскость проходит через вершину конуса, то сечением является треугольник.

Пример 6.Построить линию сечения конуса фронтально проецирующей плоскостью S (рис. 6.8).

Решение. Линией сечения в данном случае будет неполный эллипс, так как угол наклона плоскости S к оси конуса больше угла наклона образующей. Фронтальная проекция линии сечения совпадает со следом плоскости, так как секущая плоскость является фронтально проецирующей. Определим горизонтальную проекцию сечения. Первоначально отметим опорные точки: точка 1 на очерковой образующей является высшей точкой сечения, точки 2 и 3 на основании конуса – низшие точки. Ряд промежуточных точек 4, 5, 6, 7 определяем с помощью параллелей конуса, проведённых через эти точки. Точки 8, 9 определены через образующую конуса. Полученные точки плавно соединяем с учётом видимости.

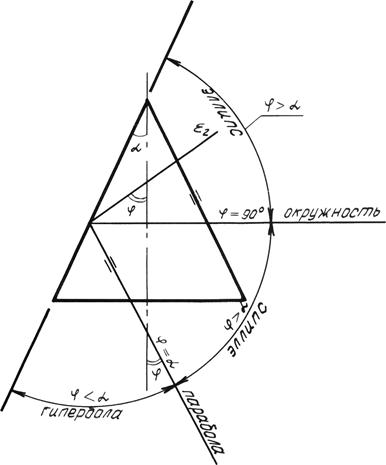
Рис. 6.7. Сечение конуса

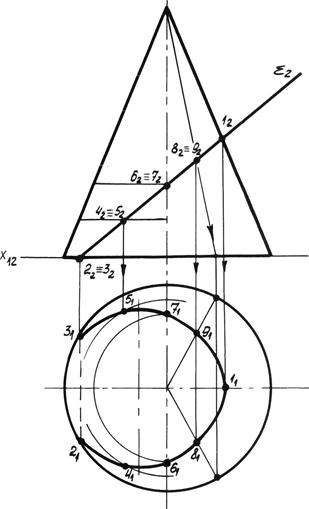
Рис. 6.8

Пример 7. Определить точки пересечения прямой а с конусом (рис. 6.9).

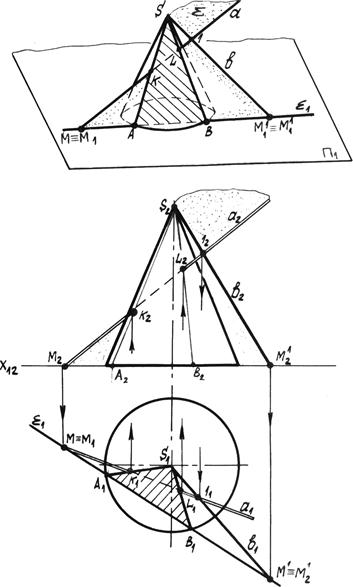
Рис. 6.9. Пересечение прямой с конусом

Решение. Для решения задачи выгоднее всего использовать вспомогательную плоскость, проходящую через вершину конуса. Для этого дополним прямую а до плоскости прямой b, пересекающейся с ней в точке 1 (см. рис. 6.9). Определим горизонтальный след вспомогательной плоскости S(а Ç b). Для этого найдём следы прямых а и b – М и М ¹. Отметим точки пересечения основания конуса с горизонтальным следом S₁ – точки А и В. Определилась линия сечения конуса со вспомогательной плоскостью – треугольник АВS.

На пересечении линии сечения A ₁ B ₁ S ₁ и проекции прямой а ₁ находим искомые точки K ₁ и L ₁, по линиям связи – точки K ₂ и L ₂. Затем определяем видимость прямой относительно точек пересечения.