1. Матричный метод.
Пусть дана система 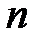 - уравнений с
- уравнений с 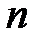 - неизвестными.
- неизвестными.
Запишем систему в виде одного матричного уравнения:
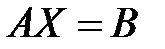 (6.1).
(6.1).
Если определитель системы 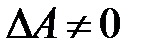 , то существует обратная матрица
, то существует обратная матрица 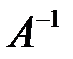 . Тогда, умножая (6.1) на
. Тогда, умножая (6.1) на 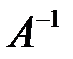 слева, получим:
слева, получим:
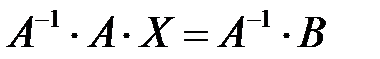 или
или 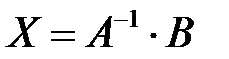 .
.
Запишем решение системы в расширенном виде:
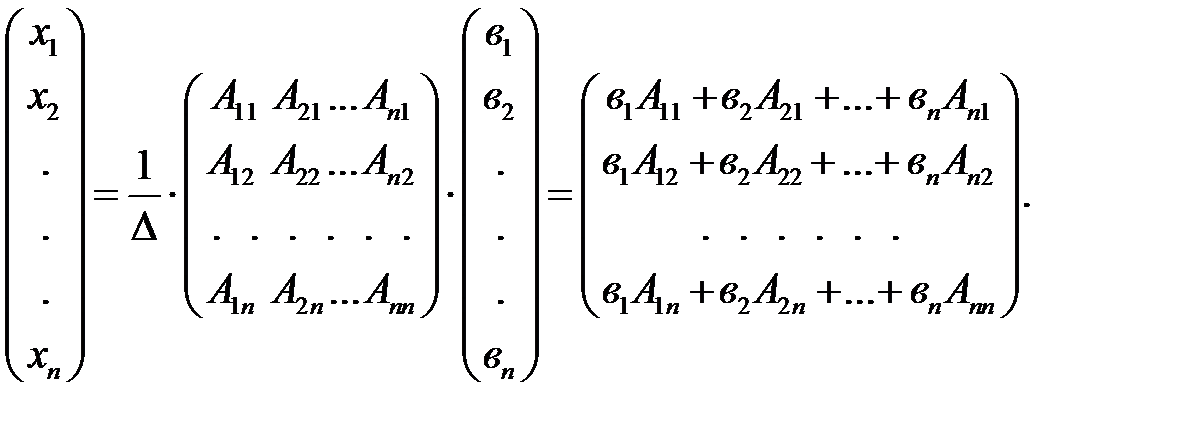
Рассмотрим полученные равенства:
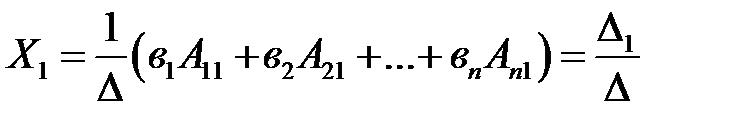 , где
, где
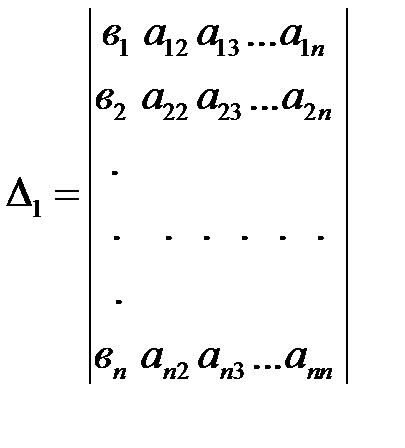
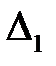 - определитель, полученный из основного определителя путем замены первого столбца столбцом свободных членов. Аналогично для всех
- определитель, полученный из основного определителя путем замены первого столбца столбцом свободных членов. Аналогично для всех  от 2 до
от 2 до 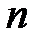 т.е.:
т.е.:
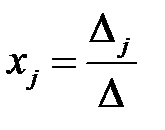 (6.2).
(6.2).
Формулы (6.2) носят название формул Крамера.
2. Метод Гаусса.
Суть этого метода состоит в последовательном исключении неизвестных.
Пример 9. Решить систему 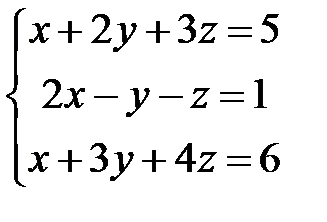
Решение. Выразим 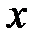 из первого уравнения системы:
из первого уравнения системы:
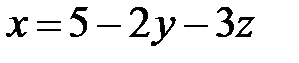 ,
,
Подставим во второе и третье уравнения:
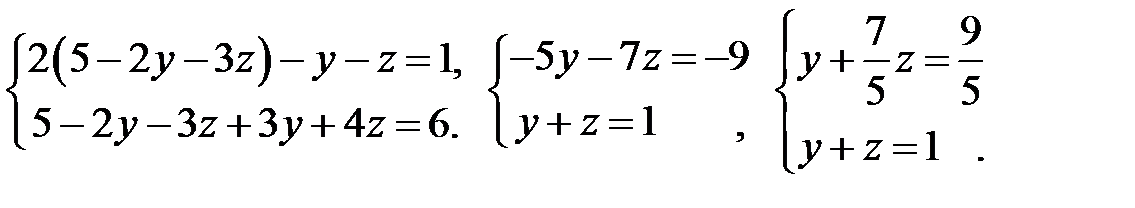
Выразим 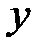 из первого уравнения полученной системы:
из первого уравнения полученной системы:
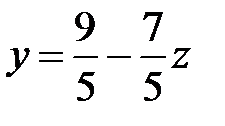 .
.
Подставим во второе уравнение:
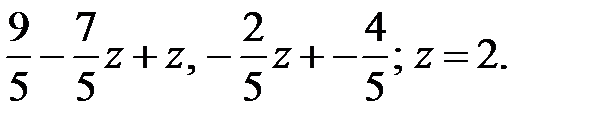
Тогда 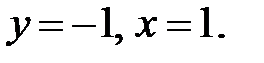
 2015-04-12
2015-04-12 363
363








