Векторы можно умножать скалярно и векторно. Скалярным произведением двух ненулевых векторов 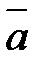 и
и 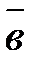 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
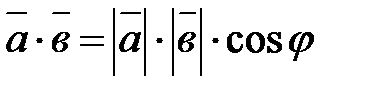 (8.1).
(8.1).
Эту формулу можно записать в виде
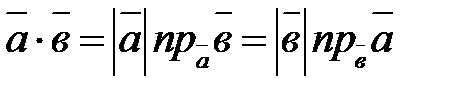 .
.
Скалярное произведение имеет следующие свойства:
1. 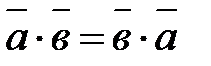 - переместительный закон.
- переместительный закон.
3. 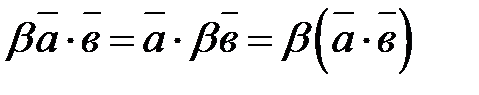
4. 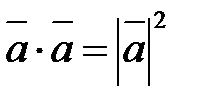 , отсюда
, отсюда 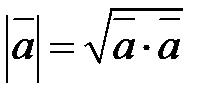
5. Если 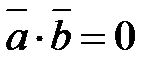 , то
, то 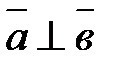 - условие перпендикулярности векторов
- условие перпендикулярности векторов 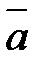 и
и 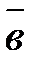
6. 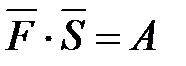 ,
, 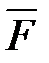 - вектор силы,
- вектор силы, 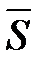 - вектор перемещения,
- вектор перемещения, 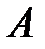 - работа силы
- работа силы 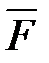 .
.
Если 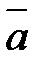 и
и 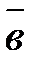 заданы в прямоугольной системе координат
заданы в прямоугольной системе координат 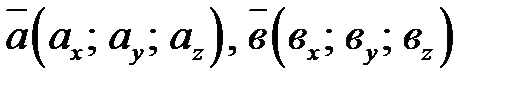 , то
, то 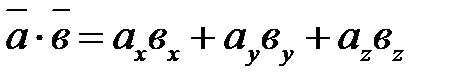 (8.2).
(8.2).
Упорядоченная тройка векторов 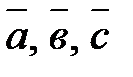 называется правой, если кратчайший поворот от вектора
называется правой, если кратчайший поворот от вектора 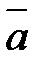 к вектору
к вектору 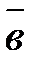 из конца вектора
из конца вектора 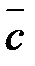 виден совершающимся против часовой стрелки. Рис.7.
виден совершающимся против часовой стрелки. Рис.7.
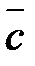 |
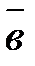 |
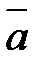 |
Рис. 7.
Векторным произведением вектора 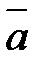 на вектор
на вектор 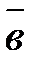 называется третий вектор
называется третий вектор 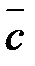 , длина которого равна
, длина которого равна 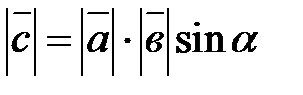 , он перпендикулярен векторам
, он перпендикулярен векторам 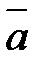 и
и 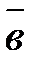 и направлен в ту сторону, что векторы
и направлен в ту сторону, что векторы 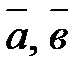 и
и 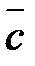 образуют правую тройку.
образуют правую тройку.
Векторное произведение обозначается 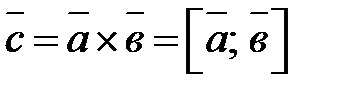 .
.
Векторное произведение имеет следующие свойства:
1. 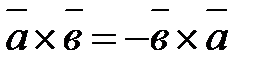
2. 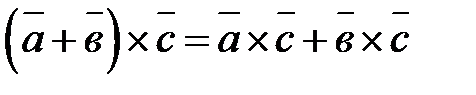
3. 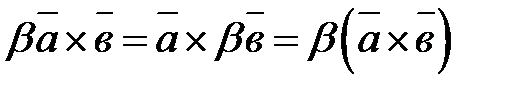
4. Если 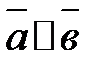 , то
, то 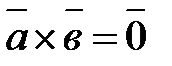
5. 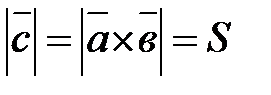 , где
, где 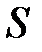 - площадь параллелограмма, построенного на этих векторах как на сторонах.
- площадь параллелограмма, построенного на этих векторах как на сторонах.
Если векторы 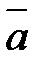 и
и 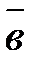 заданы в прямоугольной системе координат:
заданы в прямоугольной системе координат: 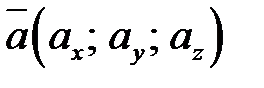 и
и 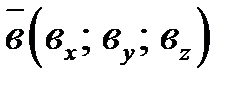 , то:
, то:
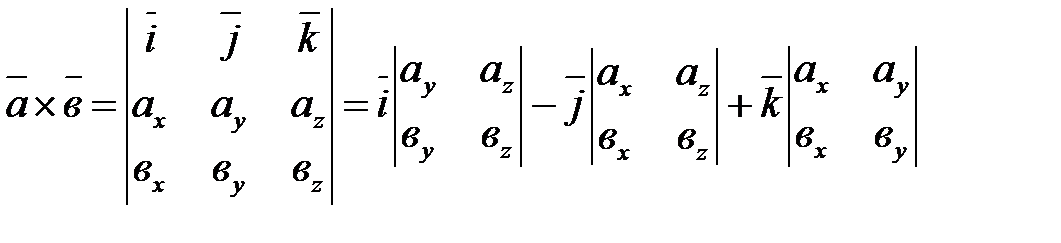 (8.3).
(8.3).
Если 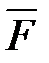 вектор силы, приложенной в точке
вектор силы, приложенной в точке 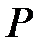 , а
, а 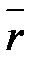 радиус-вектор точки
радиус-вектор точки 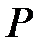 , то момент силы
, то момент силы 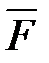 , относительно начала координат
, относительно начала координат 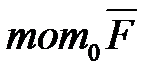 равен:
равен:
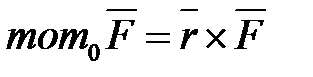 .
.
Смешанным произведением трех векторов 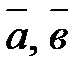 и
и 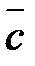 называется их векторно-скалярное произведение. Обозначается
называется их векторно-скалярное произведение. Обозначается 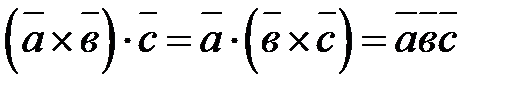 .
.
Если заданы координаты векторов в прямоугольной системе координат, то их смешанное произведение вычисляется по формуле:
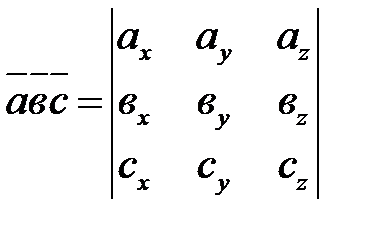 (8.4).
(8.4).
Свойства смешанного произведения векторов:
1. 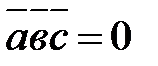 - условие компланарности векторов;
- условие компланарности векторов;
2. 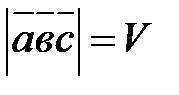 - объем параллелепипеда, построенного на векторах, как на сторонах;
- объем параллелепипеда, построенного на векторах, как на сторонах;
3. 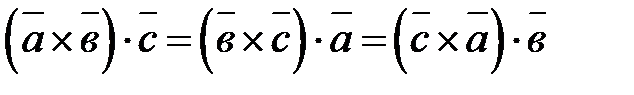 - циклическая перестановка сомножителей не меняет величины смешанного произведения;
- циклическая перестановка сомножителей не меняет величины смешанного произведения;
4. 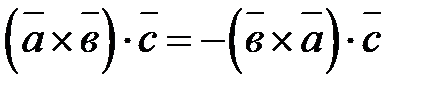
Пример 11. Даны вершины пирамиды 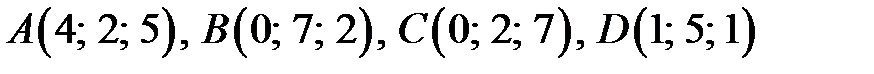 . Найти 1) угол между ребром
. Найти 1) угол между ребром 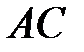 и гранью
и гранью 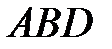 ; 2) площадь грани
; 2) площадь грани 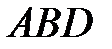 ; 3) объем пирамиды
; 3) объем пирамиды 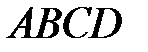 ; 4) длину высоты, опущенной из вершины
; 4) длину высоты, опущенной из вершины  на грань
на грань 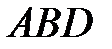 .
.
Решение. Вычислим координаты вектора 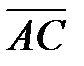 :
:
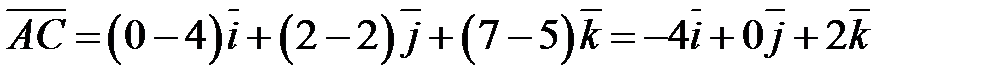 .
.
Угол 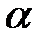 между ребром
между ребром 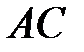 и гранью
и гранью 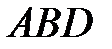 является дополнительным углом для угла
является дополнительным углом для угла 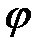 , образованного перпендикуляром, проведенным к плоскости треугольника
, образованного перпендикуляром, проведенным к плоскости треугольника 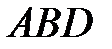 и ребром
и ребром 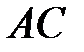 .
. 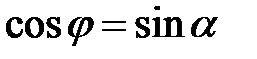 . Для нахождения
. Для нахождения 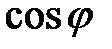 вычислим координаты векторного произведения векторов
вычислим координаты векторного произведения векторов 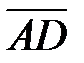 и
и 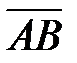 :
:
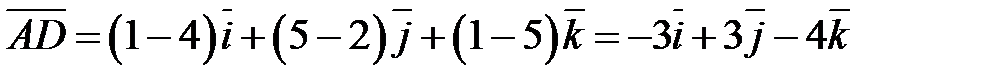 ;
;
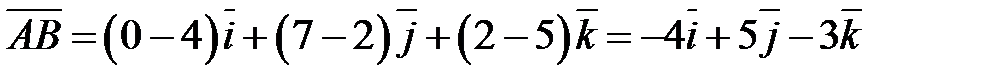 .
.
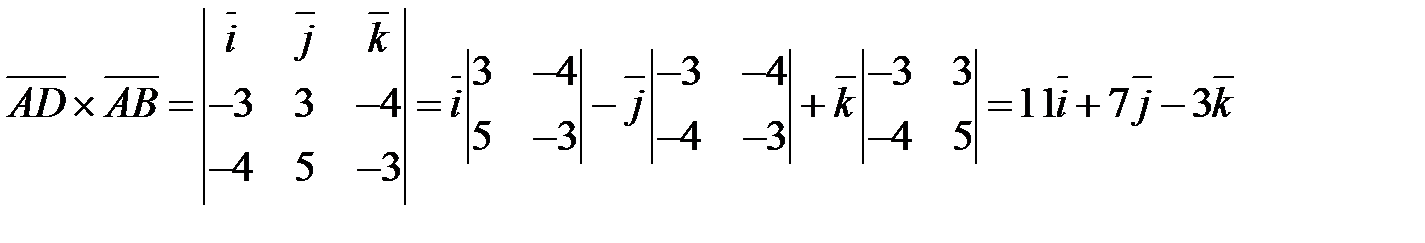 .
.
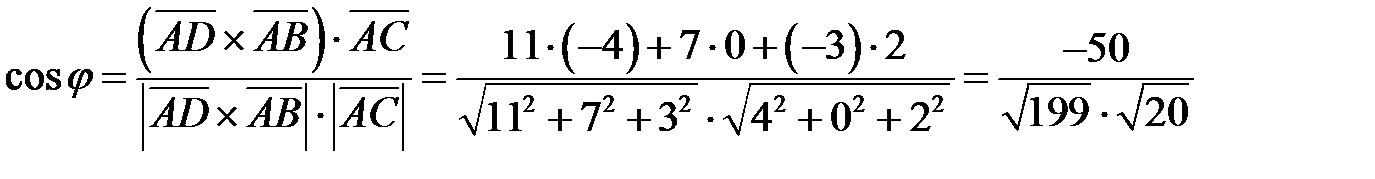 ;
;
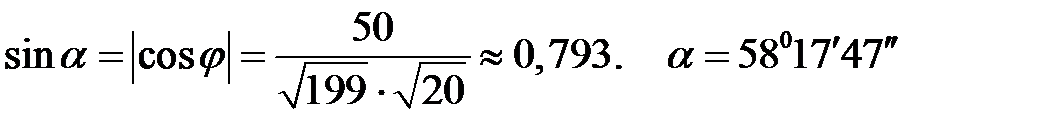 .
.
1) Площадь грани 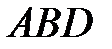 равна половине площади параллелограмма, построенного на сторонах
равна половине площади параллелограмма, построенного на сторонах 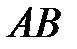 и
и 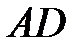 , т.е.
, т.е.
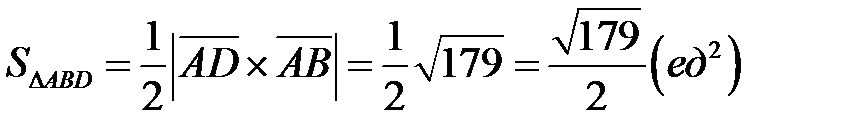 .
.
2) Объем пирамиды равен одной трети от объема параллелепипеда,
построенного на ребрах 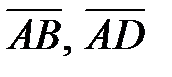 и
и 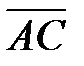 . Следовательно
. Следовательно
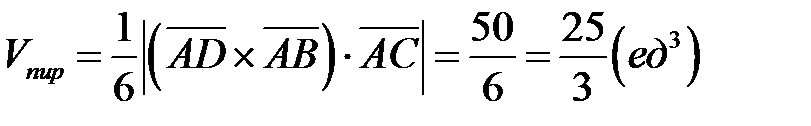 .
.
3) Длина высоты 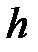 определяется из формулы:
определяется из формулы:
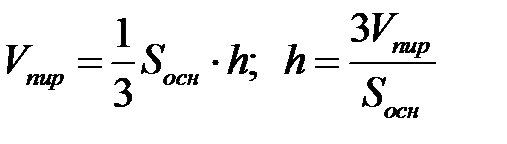 ;
; 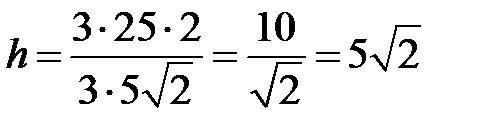 .
.
Ответ: 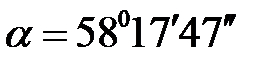 ;
; 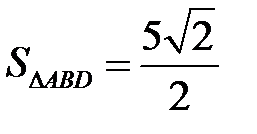 ;
; 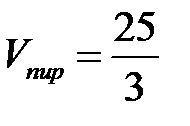 ;
; 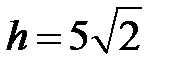 .
.
 2015-04-12
2015-04-12 5068
5068

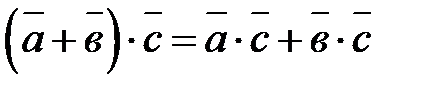 -
-