Элементарные операции

Простейшие операции, с помощью которых из базовых функций могут быть получены рекурсивные функции, называют элементарными.

К числу элементарных операций относят операции суперпозиции, рекурсии и минимизации.

Операция суперпозиции. Если даны функция h от m независимых переменных аргумента, т.е. h = (z₁; z₂;... z_m; у), и m функций q_i от n независимых переменных аргумента, т.е. {q_i=(x_1i; x_2i;... x_ni; z_ij)}, то в результате подстановки функций q₁, q₂... q_m вместо аргументов функции h может быть получена новая функция f=(x₁; x₂;... x_n; у) от n независимых переменных аргумента, т.е.

h = (z₁; z₂:... z_m; y):

q₁ = (x₁; x₂;... x_n; z₁);

q₂ = (x₁; x₂;... x_n; z₂);

...................................

q_m = (x₁; x₂;... x_n; z_m);

h = (q₁; q₂;... q_m; y) = f = (x₁; x₂;... x_n; y).

Значения функций q₁; q₂;... q_n, найденные при заданных значений независимых переменных x₁; x₂;... x_n, принять за значения независимых переменных аргумента функции h и вычислить ее значение, которое принять за значение функции f = (x₁; x₂;... x_n; y).

Например, если h = (z; y) = l(z) и q(х; z) = l(х), то f=(q; у) = l(l) = l²(х). Следовательно, для х = 5 имеем z=5 + 1= = 6 и у = 6 + 1 = 7.

Оператор суперпозиции, реализующий одноименную операцию, часто записывают так:

f = x₁; x₂;... x_n; y = S_mⁿ (h^(m); q₁⁽ⁿ⁾; q₂⁽ⁿ⁾;... q_m⁽ⁿ⁾),

где h^(m) =(z₁; z₂;... z_m; y) и

q₁⁽ⁿ⁾ = (x_1i ⁽ⁿ⁾; x_2i ⁽ⁿ⁾;... x_ni ⁽ⁿ⁾; z_i).

Если заданы функции тождества (I_n,m) и оператор суперпозиции (S_mⁿ), то можно считать заданными всевозможные операторы подстановки, перестановки и переименования любых функций.

Операция рекурсии. Если даны n-местная рекурсивная функция g и (n + 2)-местная рекурсивная функция h, то можно найти (n + 1)-местную рекурсивную функцию f, используя схему примитивной рекурсии:

f (x₁; x₂;... x_n; 0) = g (x₁; x₂;... x_n;);

f (x₁; x₂;... x_n; у+1) = h (x₁; x₂;... x_n; у; f(x₁; x₂;... x_n; у)).

Схема примитивной рекурсии позволяет определить значения функций f не только через значения функций g и h, но и через значения функций f во всех предшествующих точках аргумента.

Схема примитивной рекурсии содержит главный дополнительный аргумент – у, который войдет в значение определяемой функции, и один вспомогательный аргумент – f (x₁; x₂;... x_n; у), который позволяет определить значение искомой функции для последующих значений главного дополнительного аргумента.

Оператор рекурсии, реализующий одноименную операцию, записывают так:

f = (x₁; x₂;... x_n; у+1) = R(g⁽ⁿ⁾; h⁽ⁿ⁺²⁾),

где g_i⁽ⁿ⁾ = g_i (x₁; x₂;... x_n;);

h⁽ⁿ⁺²⁾ = h (x₁; x₂;... x_n; у; f (x₁; x₂;... x_n; у)).

Переменные x₁; x₂;... x_n при выполнении операции рекурсии играют роль фиксированных параметров, т.е.

x₁ = a_i; x₂ = a₂;... x_n = а_n.

Итак, значением искомой функции f для нулевого значения главного дополнительного аргумента следует считать значение исходной функции g, значением функции f для каждого последующего значения главного аргумента (у+1) следует считать значения функции h при предыдущих значениях главного аргумента у и при значении вспомогательного аргумента, совпадающим с предыдущим значением искомой функции.

Пример. Пусть g (х) = C_i (х) = 0; h (х; у; f (х; у)) = J_3,2 = y. Тогда по схеме примитивной рекурсии имеем:

f (х, 0) = g (х) = 0;

f (х; у+1) = h (х; у; f (х; у)) = у;

Так как функции g и h не содержат в качестве аргумента независимую переменную х, то имеем:

f(0) = 0;

f(1) = 0;

f(2) = 1;

f(3) = 2;

..............

f (i) = (i - 1); если i = у, то f (у) = (у– 1) = l(у).

Пусть у = 6, тогда f (6) = 6 – 1 = 5.

Так как рекурсивная функция принимает значения на множестве целых положительных чисел, то функция предшествования реализует усеченное вычитание, формула которого имеет вид:

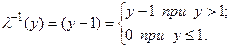
Таким образом, в дополнение функции следования получена функция предшествования. Для получения функции предшествования использованы две базовые функции (константа и тождества) и операция примитивной рекурсии: (у – 1) =R (0; у) = l^-1 (у).

Пример. Пусть g(x)=J_1,1=x;

h (х; у; f (х; у)) = l (J_3,3) = f (x; у) + 1.

По схеме примитивной рекурсии имеем:

f (х; 0) = g(х) = х;

f (х; 1) = h (x; 0; f (x; 0)) = x + 1;

f (x; 2) = h(x; 1; f(x; 1)) = x + 2;

f (x; 3) = h (x; 2; f (x; 2)) = x + 3;

......................................................

f (x; i) = h (x; (i – 1); f (x; (i – 1))) = x + i; если i = у, то f(x;у)=(x+у).

Пусть x = 3, у = 6, тогда f (3; 6) = 3 + 6 = 9.

Таким образом, для получения значений функции сложения двух независимых переменных использованы две базовые функции (тождества и следования) и операция примитивной рекурсии:

(х + у) = R (х; (f (х; у) + 1)) = f₊ (х; у).

Пример. Пусть g(x) = I_1,1 = x;

h (х; у; f (х; у)) = l^-1 (J_3,3) = f (x; у) – 1.

По схеме примитивной рекурсии имеем:

f (х; 0) = g(х) = х;

f (х; 1) = h (x; 0; f (x; 0)) = x – 1;

f (x; 2) = h(x; 1; f(x; 1)) = (x – 1) – 1 = x – 2;

f (x; 3) = h (x; 2; f (x; 2)) = (x – 2) – 2 = x – 3;

......................................................................

f (x; i) = h (x; (i – 1); f (x; (i – 1))) = (x – (i – 1)) – 1 = x – 1.

Если i = у, то f (x; у) = (x – у).

Пусть х = 6, y = 3, тогда f (6; 3) = 6 – 3 = 3.

Формула усеченного вычитания имеет следующие значения:

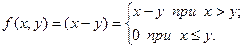
Таким образом, для получения значений функции вычитания двух независимых переменных использованы базовая функция тождества, примитивно рекурсивная функция предшествования и операция примитивной рекурсии:

(х – у) = R (х; (l^-1 (f(х; у))) = f₊ (х; у).

Пример. Пусть g(x) = С₁ = 0;

h (х; у; f (х; у)) = f₊ (J_3,1 ; J_3,3 ) = x + f (x; у).

По схеме примитивной рекурсии имеем:

f (х; 0) = g(х) = 0;

f (х; 1) = h (x; 0; f (x; 0)) = x + 0 = x;

f (x; 2) = h(x; 1; f (x; 1)) = (x + x) = 2x;

f (x; 3) = h (x; 2; f (x; 2)) = (x + 2x) = 3x;

..................................................................

f (x; i) = h (x; (i – 1); f (x; (i –1))) = (x + (i – 1)) – x = i – x.

Если i = у, то f (x; у) = x ^. у.

Пусть х = 3, y = 4, тогда f (3; 4) = 3 ^. 4 = 12.

Таким образом, для получения значений функции умножения двух независимых переменных использованы базовая функция константы и примитивно рекурсивная функция сложения:

x ^. у = R (0; f₊ (х; f (x; у))) = f₊ (х; у).

Пример. Пусть g(x) = С₁ = 1;

h (х; у; f (х; у)) = f _* (J_3,1 ; J_3,3 ) = x ^. f (x; у).

По схеме примитивной рекурсии имеем:

f (х; 0) = g (х) = 1;

f (х; 1) = h (х; 0; f (х; 0)) = х ^. 1= х;

f(x; 2) = h (x; 1; f (х; l)) x ^. x = x²;

f (õ; 3) = h (õ; 2; f (õ; 2)) = х ^. x² = x³;

..........................................................

f (x; i) = h (x; (i - 1); f (x; (i - 1))) = x ^. x^{(i - 1)} = xⁱ.

Если i = у, то f (x; y) = x^y.

Пусть x = 3, у = 3, тогда f (3; 3) = 3³ = 27.

Таким образом, для получения значений функции возведения в степень использованы базовая функция константы и примитивно рекурсивная функция умножения:

х^y = R (1; f_* (x; f (x; y)))=f_exp(x; y).

Из приведенных примеров легко можно получить примитивно рекурсивные функции:

a) min (х; у) = х – (х – у);

б) mах (х; у) = у – (х – у);

в) | х – у| = (х – у) + (у – х);

г) х = 1 – х;

д) х v у = mах (х; у);

е) х ^. у = min (х; у).

Функции, для вычисления значений которых использовали базовые функции и операторы суперпозиции и примитивной рекурсии, называют примитивно рекурсивными функциями. Последовательность рекурсивного описания функции, использующая базовые функции и результаты вычисления ее значений на всех предшествующих точках с помощью операторов суперпозиции и примитивной рекурсии, называют протоколом вычисления значения функции.

Примеры. 1. Доказать, что функция 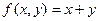является примитивно-рекурсивной.

Решение. Так как данная функция 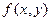есть функция двух аргументов, то для использования операции примитивной рекурсии мы должны иметь функцию g, зависящую от одного аргумента, и функцию h, зависящую от трех аргументов. Определим их.

В функции 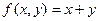положим y =0. Тогда имеем 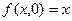- это тождественная функция. Полагая y =1, получим 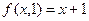- это функция следования.

Таким образом, выбираем следующие элементарные функции: тождественную 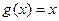и функцию следования 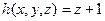. Заметим, что здесь .

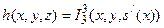Используем схему примитивной рекурсии:

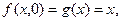
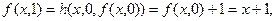
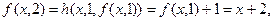
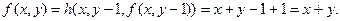
Таким образом, построена функция (таблица ее значений) которая равна сумме двух слагаемых.

2. Доказать, что функция 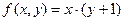является примитивно-рекурсивной.

Решение. Заметим, что

.

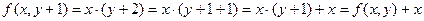Найдем требуемые функции 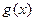и h. Для этого считаем, что, так как заданная функция 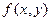есть функция двух аргументов, следует выбрать функцию g, зависящую от одного аргумента, и функцию h, зависящую от трех аргументов.

Для заданной функции можно записать

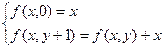
Первая из этих функций – это тождественная функция 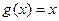, а вторая определяет функцию h. Это функция сложения двух чисел, которая, как доказано выше, является примитивно-рекурсивной. Поэтому можно использовать ее для выбора функции h.

Итак, имеем для операции примитивной рекурсии:

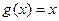- функция одного аргумента,

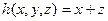- функция трех аргументов.

Проверим, что функции выбраны правильно. Из определения операции примитивной рекурсии имеем:

…………………..

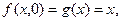
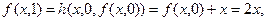
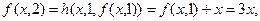
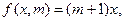
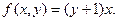
Примитивно-рекурсивность операции умножения доказана. Этот факт можно использовать при доказательстве примитивной рекурсивности других функций.

3. Найти функцию 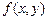, полученную из функци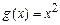й и 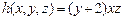по схеме примитивной рекурсии.

Решение. Найдем несколько значений функции f:

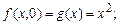
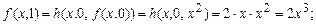
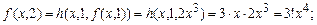
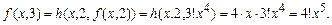
Сделаем предположение, что

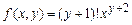. (1)

Докажем формулу (1) методом математической индукции, проведя индукцию по y:

1) Проверка при y =0.

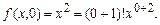
Да, при y =0 формула (1) верна.

2) Допустим, что формула (1) верна при y = n, т.е. допустим, что верно

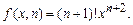(2)

3) Докажем, что формула (1) верна при y = n+ 1, т.е. докажем справедливость формулы

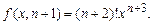(3)

Выразим 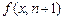с помощью схемы примитивной рекурсии:

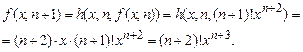
Итак, в предположении справедливости формулы (2) доказана формула (3). На основании метода математической индукции утверждаем, что предположении (1) справедливо для всех .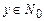

Ответ: .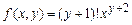

Операция минимизации (поиск наименьшего корня). Если дана (n + 1)-местная функция f(x₁; x₂;... x_n; у), то значение n-местной функции j(x₁; x₂;... x_n) можно определить, придавая вспомогательному аргументу у последовательно значения 0; 1; 2; 3;..., пока не окажется, что функция f (x₁; x₂;... x_n; у) в первый раз стала равной нулю, т.е. f(x₁; x₂;... x_n; у) = 0. Полученное значение вспомогательного аргумента у принять за значение определяемой функции, соответствующей заданным значениям независимых переменных аргумента (x₁ = a₁; x₂ =a₂;... x_n = a_n), при которых выполнялся вычислительный процесс.

Поиск значений функции j (x₁; x₂;... x_n) может быть задан с помощью m-оператора, который может быть записан так:

j (x₁; x₂;... x_n) = m_y (f (x₁; x₂;... x_n; y) = 0.

Операция минимизации по i -ой переменной функции 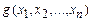обозначается 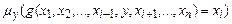и определяется следующим образом:

Рассмотрим соотношение

, (*)

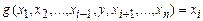которое будем рассматривать как уравнение относительно y. Это уравнение будем решать подбором, подставляя вместо y числа 0, 1, 2 и т.д. Возможны случаи:

1) на некотором шаге левая часть соотношения (*) не определена. В этом случае считаем, что на наборе 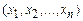операция минимизации не определена;

2) на каждом шаге левая часть соотношения (*) определена, но ни при каких y равенство не выполняется. В этом случае также считаем, что на наборе 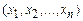операция минимизации не определена;

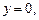
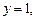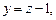
3) левая часть соотношения (*) определена при …, 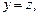но при 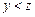равенство (*) не выполняется, а при 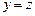оно выполняется. В этом случае число z считается значением операции минимизации на наборе .

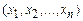Пример. Найти функции, получаемые из числовой функции 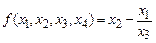с помощью операции минимизации по каждой ее переменной.

Решение.

1. Минимизируем данную функцию по переменной 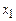. Рассмотрим уравнение 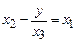. (4)

а) Если 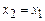, то при подстановке вместо y нуля получаем верное равенство.

б) Если 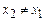, , 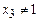то при подстановке в уравнение (4) вместо y единицы в левой части уравнения (4) появляется неосмысленное выражение – дробь 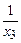, значит, в этом случае операция минимизации не определена.

в) Если 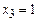, но 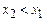, уравнение (4) примет вид 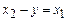. Это уравнение не может выполниться ни при каких .

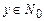г) Если 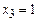, но 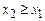, то при 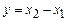уравнение (4) выполнится.

Итак,

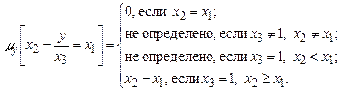
2. Минимизируем данную функцию по переменной 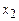. Рассмотрим уравнение 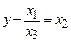. (5)

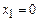Если , а 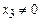, то уравнение (5) примет вид 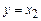и имеем решением число .

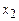Если 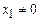, то на самом первом шаге, при подстановке вместо y нуля, в левой части уравнения (5) возникает отрицательное число, т.е. неосмысленное выражение.

Итак,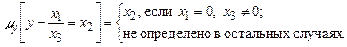

3. Минимизируем данную функцию по переменной 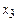. Рассмотрим уравнение 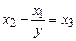. (6)

Это уравнение на самом первом шаге, при подстановке вместо y нуля теряет смысл, операция минимизации по переменной 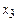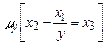нигде не определена.

4. Минимизируем данную функцию по переменной 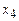. Рассмотрим уравнение 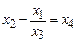. (7)

Если набор переменных таков, что левая часть уравнения (7) имеет смысл и уравнение выполнимо, то можно считать, что оно выполнимо при подстановке в (7) переменной y на самом первом шаге, т.е. при y =0.

В остальных случаях значение операции минимизации не определено. Итак,

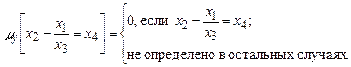
Использование оператора m_y-удобное средство для поиска обратных рекурсивных функций.

Как правило, область определения функции j (x₁; x₂;... x_n) меньше области определения функции f (x₁; x₂;... x_n; у), что позволяет утверждать о частичной рекурсивности функции j(x₁; x₂;... x_n).

Пример. Пусть f (x₁; x₂;... x_n; у) = f (x; у) = y² – x.

Тогда j (x) = m_y (j (x; y) = y²–x = 0 или j (x) =y = .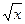

Так как j (x) является рекурсивной функцией, то 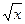должен иметь только целое положительное значение. Таким образом, j (x) определена только для значения х = 1, 4, 9, 16... и имеет значение, соответственно, 1, 2, 3, 4,... Таким образом, функция j (x) также является частично рекурсивной.

Если дан алгоритм вычисления функции f (a₁; a₂;... a_n; у), то значение функции j (a₁; a₂;... a_n) вычисляется следующим образом:

шаг 1: принять у = 0 и вычислить значение функции f (a₁; a₂;... a_n; у).

шаг 2: если f (a₁; a₂;... a_n; у) = 0, то конец, значение функции j (a₁; a₂;... a_n) = у, иначе принять у = у + 1 и перейти к шагу 1.

Пример. Пусть f (a₁; a₂;... a_n; у)=(x₁ – x₂ – x₃ – y), где x₁ = 7, x₂ = 1, x_з = 2.

Тогда по алгоритму минимизации имеем:

f =(7; 1; 2; 0) = 7 – 1 – 2 – 0 ¹ 0;

f = (7; 1; 2; 1) = 7 – 1 – 2 – 1 ¹ 0;

f = (7; 1; 2; 2) = 7 – 1 – 2 – 2 ¹ 0;

f = (7; 1; 2; 3) = 7 – 1 – 2 – 3 ¹ 0;

f = (7; 1; 2; 4) = 7 – 1 – 2 – 4 = 0.

Следовательно, j (x₁; x₂;... x_n) = j (7; 1; 2) = 4.

Операция итерации. Повторное выполнение какого-либо процесса до тех пор, пока не будет удовлетворено заданное условие, называют итерацией. При этом выполнение процесса производится каждый раз полностью. Однократное выполнение процесса называют шагом итерации.