Часто при проведении анкетирования или тестирования рассматриваются только два значения переменной, например «0» и «1» («нет» или «да»). Возникает ситуация т.н. «дихотомического оценивания». Пусть группа вопросов анкеты посвящена исследованию одного признака. Задачей корреляционного анализа в этом случае может быть оценка тесноты связи между вопросами анкеты, принадлежащими данной группе, а целью – оценка качества самой анкеты в отношении исследования рассматриваемого признака.
В простейшем учебном варианте дихотомического оценивания изучают тесноту связи только двух вопросов. В качестве переменных рассматривают ответы на вопросы анкеты Х и У со значениями «0» и «1». Эти ответы были даны группой респондентов или тестируемых. Исходной в таком случае является матрица корреляции
| У Х | ||
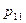 
| 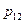
| |
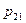
| 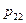
|
Здесь 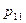 – процентная доля респондентов, ответивших «0» на оба вопроса,
– процентная доля респондентов, ответивших «0» на оба вопроса, 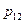 – процентная доля респондентов, ответивших «0» на вопрос Х и «1» на вопрос У и т.д. Выполняется условие нормировки
– процентная доля респондентов, ответивших «0» на вопрос Х и «1» на вопрос У и т.д. Выполняется условие нормировки
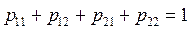 . (17.1)
. (17.1)
Построим ряды распределения случайных величин Х и У по отдельности. Для этого складываем элементы корреляционной матрицы по столбцам и по строкам:
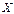
| 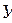
| |||||
| Р | 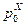
| 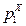
| Р | 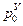
| 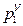
|
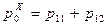 ,
, 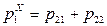 ,
, 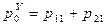 ,
, 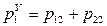 (17.2)
(17.2)
Находим параметры, аналогичные определенным формулами (16.1) – (16.8). Математические ожидания вычисляются по формулам (5.2)
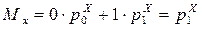 ; (17.3)
; (17.3)
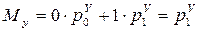 . (17.4)
. (17.4)
Дисперсии вычисляются по формуле (5.3)
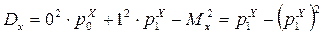 ; (17.5)
; (17.5)
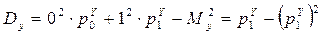 . (17.6)
. (17.6)
Средне квадратические отклонения вычисляются по формулам (5.4)
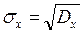 ,
, 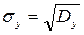 .(17.7)
.(17.7)
Ковариация вычисляется по формуле
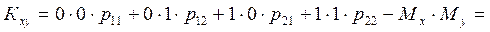
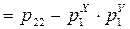 . (17.8)
. (17.8)
Коэффициент корреляции вычисляется по формуле
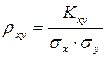 . (17.9)
. (17.9)
При дихотомическом оценивании принимается обычно градация степеней корреляции, отличная от приведенной в разд. 16 (табл. 17.1).
Таблица 17.1.
 2015-04-12
2015-04-12 456
456








