7.1. Рассчитывается среднеожидаемое значение функции полезности по каждой альтернативе:
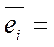 {
{ 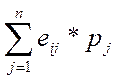 } используем метод Байеса
} используем метод Байеса
7.2. Рассчитывается среднеквадратическое отклонение:
σi 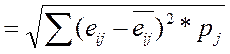
7.3. Определяем коэффициент вариации: 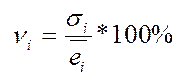
В рассм. примере p1=0,4 p2=0,2 p3=0,1 p4=0,3
| Z1 | Z2 | Z3 | Z4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Полученные показатели сводим в таблицу:
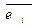 (МЕТОД Байеса) (МЕТОД Байеса) | σi | νi | |
| А1 | 35,8% | ||
| А2 | 28,3% | ||
| А3 | 44,75% |
где σi (А1)= 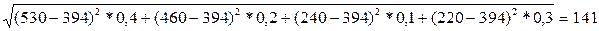
Следовательно, e (А*) = min {νi (А)}= e (А2)
 2015-04-12
2015-04-12 756
756








