Стандартное отклонение и дисперсия

4.1.1. Описание

Важнейшей мерой рассеяния является дисперсия. При ее вычислении определяются отклонения значений призна­ка или, соответственно, середин классов от арифметического среднего и возводятся в квадрат. Последнее действие обусловлено двумя причинами:

• желанием исключить влияние знака;

• необходимостью сделать чрезмерно большие отклонения еще заметнее.

Итак, дисперсия определяется следующим образом.

I) Для негруппированных значений признака:

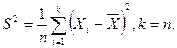
2) Для группированных значений признака:

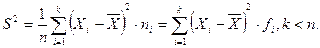
Выражение 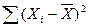характеризуется как сумма квадратов отклонений. Квадратный корень в дисперсии вытекает так называемое стандартное отклонение:

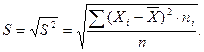
В то время как в теоретической статистике находит применение главным образом дисперсия как мера рассеяния, в практической статистике используется преимущественно стандартное отклонение.