Существует ещё один приближенный, но достаточно точный при больших значениях n способ вычисления вероятностей 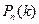 .
.
Теорема Лапласа. Пусть p - вероятность появления события А в одном испытании, причем 0 < p < 1. Тогда вероятность того, что в условиях схемы Бернулли в n испытаниях
событие А наступит ровно k раз, приближенно выражается равенством:
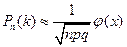 , где
, где 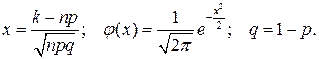 (12.1)
(12.1)
Формула (1) дает тем более точный результат, чем больше n.
Функция 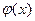 чётная, поэтому для неё составлены таблицы только при
чётная, поэтому для неё составлены таблицы только при 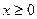 .
.
Замечание: Рекомендуется применять локальную теорему Лапласа, когда 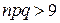 , приближение Пуассона, когда
, приближение Пуассона, когда 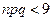 .
.
 2015-04-12
2015-04-12 471
471








