Задание 1. Найти все лорановские разложения данной функции по степеням

Найти все лорановские разложения данной функции по степеням 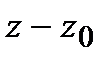. Указать главную и правильную части ряда.

= ,

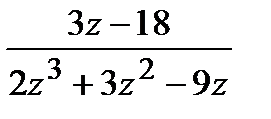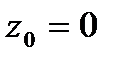
Задание 2. Для функции 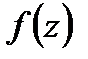найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

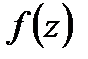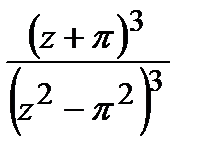
Задание 3. В ычислить интеграл от функции комплексного переменного:

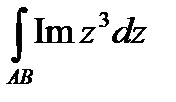; АВ – отрезок прямой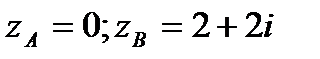

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 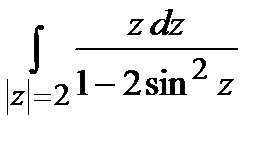; б) .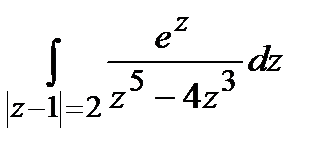

Задание 5. Вычислить интегралы с помощью вычетов.

1.

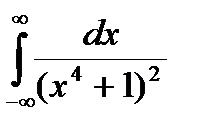
2.

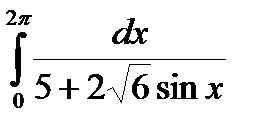
Вариант №4

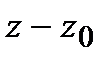Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= ,

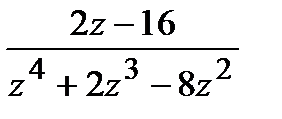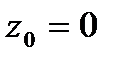
Задание 2. Для функции 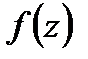найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

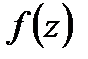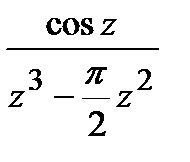
Задание 3. В ычислить интеграл от функции комплексного переменного:

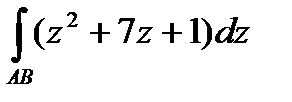; АВ – отрезок прямой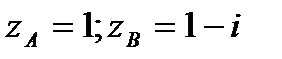

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 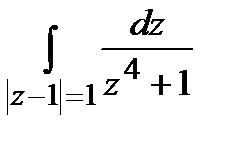; б) .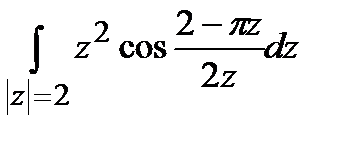

Задание 5. Вычислить интегралы с помощью вычетов.

1.

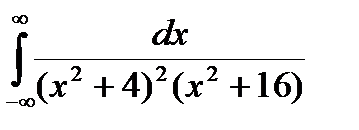
2.

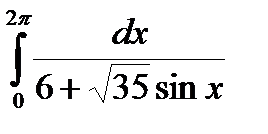
Вариант №5

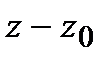Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

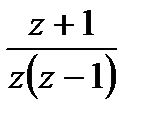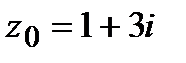Задание 2. Для функции 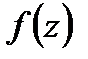найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= .

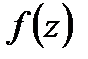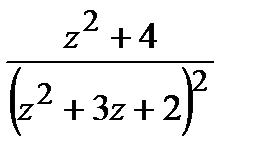Задание 3. В ычислить интеграл от функции комплексного переменного:

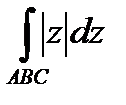; АВС – ломаная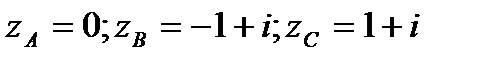

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 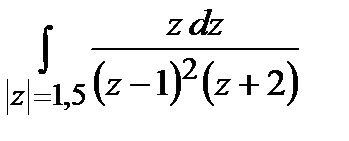; б) .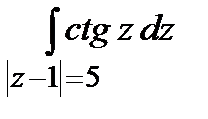

Задание 5. Вычислить интегралы с помощью вычетов.

1.

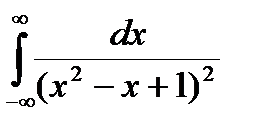
2.

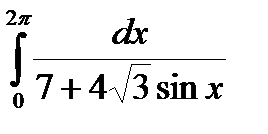
Вариант №6

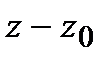Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , ;

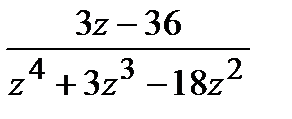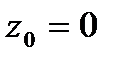Задание 2. Для функции 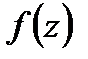найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= ;

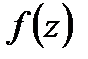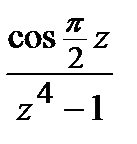Задание 3. В ычислить интеграл от функции комплексного переменного:

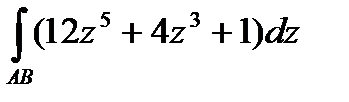; АВ – отрезок прямой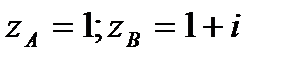

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 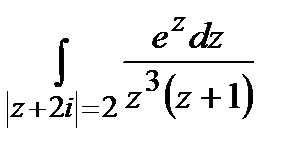; б)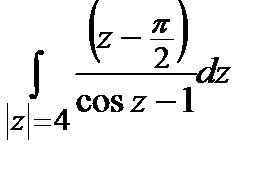

Задание 5. Вычислить интегралы с помощью вычетов.

1.

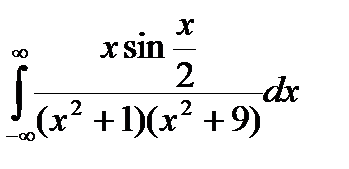
2.

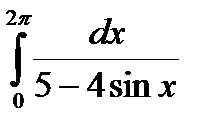
Вариант №7

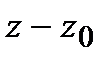Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

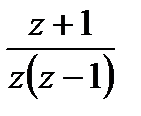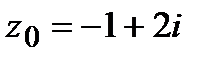Задание 2. Для функции 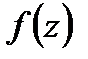найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

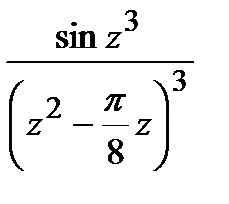
Задание 3. В ычислить интеграл от функции комплексного переменного:

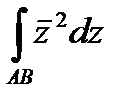; АВ – отрезок прямой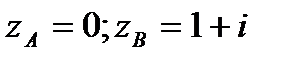

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 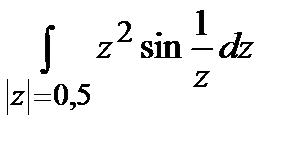; б) .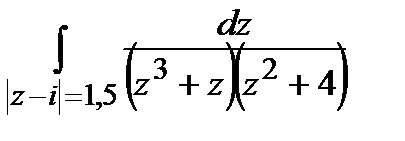

Задание 5. Вычислить интегралы с помощью вычетов.

1.

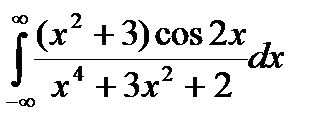
2.

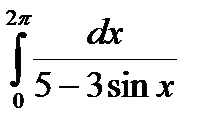
Вариант №8

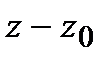Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= ,

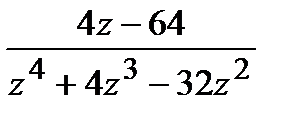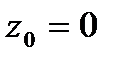
Задание 2. Для функции 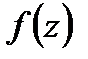найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= .

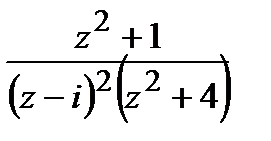Задание 3. В ычислить интеграл от функции комплексного переменного:

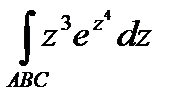; АВС – ломаная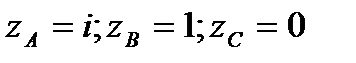

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 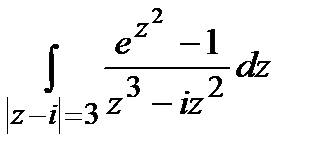; б) .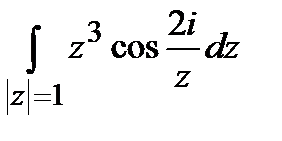

Задание 5. Вычислить интегралы с помощью вычетов.

1.

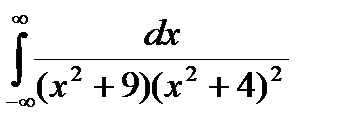
2.

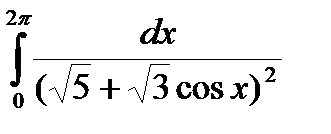
Вариант №9

Задание 1. Найти все лорановские разложения данной функции по степеням 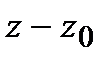. Указать главную и правильную части ряда.

= , .

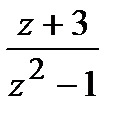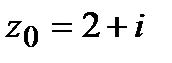Задание 2. Для функции 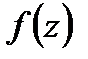найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

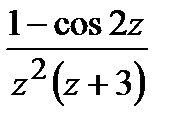
Задание 3. В ычислить интеграл от функции комплексного переменного:

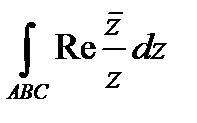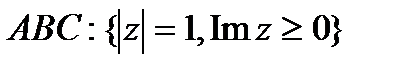; , BC- отрезок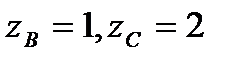

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 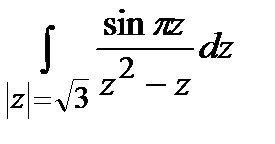; б) .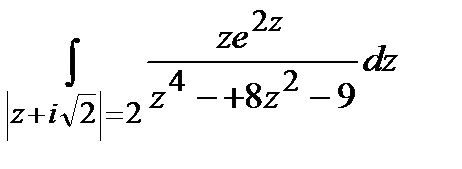

Задание 5. Вычислить интегралы с помощью вычетов.

1.

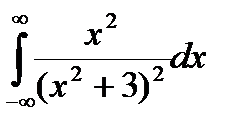
2.

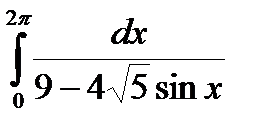
Вариант №10

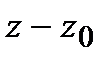Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

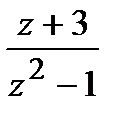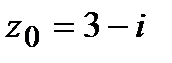Задание 2. Для функции 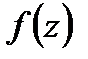найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= .

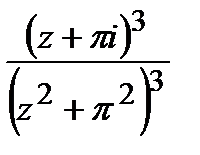Задание 3. В ычислить интеграл от функции комплексного переменного:

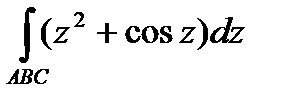; АВС – ломаная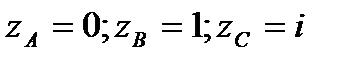

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 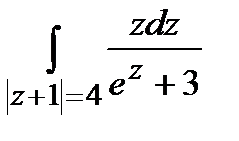; б) .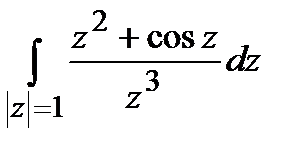

Задание 5. Вычислить интегралы с помощью вычетов.

1.

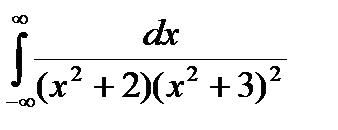
2.

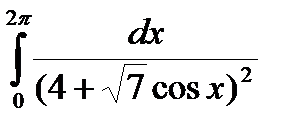
Вариант №11

Задание 1. Найти все лорановские разложения данной функции по степеням 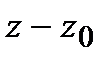. Указать главную и правильную части ряда.

= , .

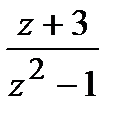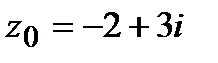Задание 2. Для функции 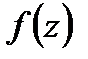найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= ;

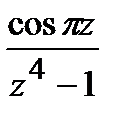Задание 3. В ычислить интеграл от функции комплексного переменного:

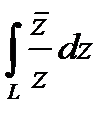; L –граница области: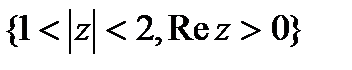

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 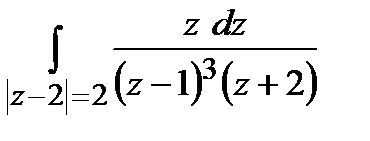; б) .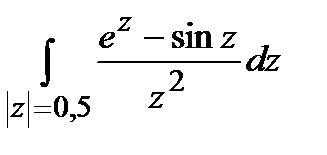

Задание 5. Вычислить интегралы с помощью вычетов.

1.

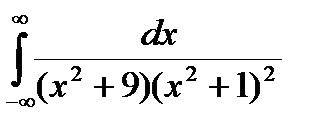
2.

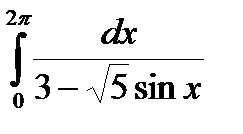
Вариант №12

Задание 1. Найти все лорановские разложения данной функции по степеням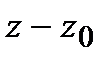

= ,

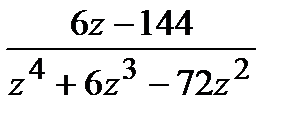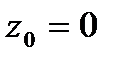
Задание 2. Для функции 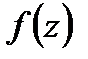найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= .

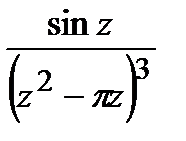Задание 3. В ычислить интеграл от функции комплексного переменного:

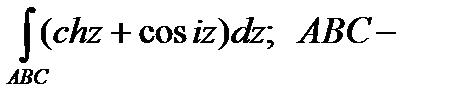ломаная, .

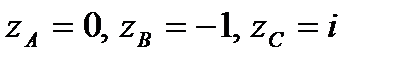Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 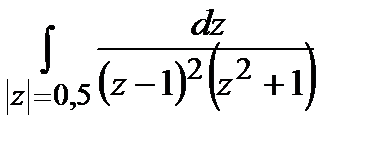; б) .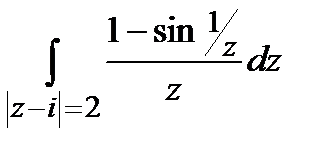

Задание 13. Вычислить интегралы с помощью вычетов.

1.

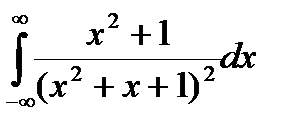
2.

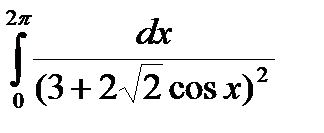
Вариант №13

Задание 1. Найти все лорановские разложения данной функции по степеням 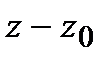. Указать главную и правильную части ряда.

= , .

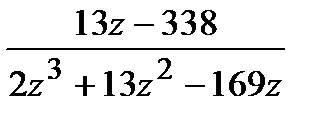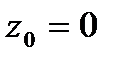Задание 3. Для функции 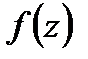найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

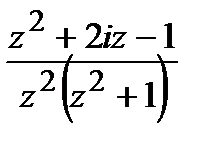
Задание 3. В ычислить интеграл от функции комплексного переменного:

.

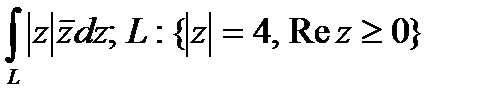Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 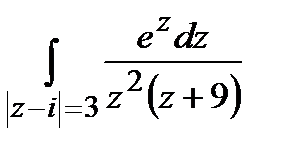; б) .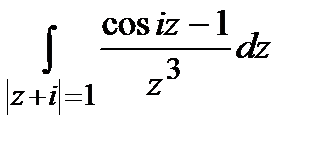

Задание 5. Вычислить интегралы с помощью вычетов.

1.

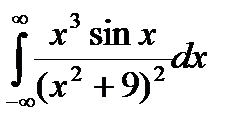
2.

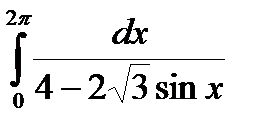
Вариант №14

Задание 1. Найти все лорановские разложения данной функции по степеням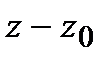

а) = , ;

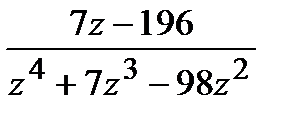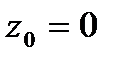Задание 2. Для функции 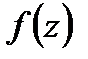найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

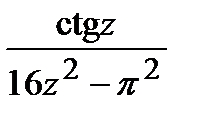
Задание 3. В ычислить интеграл от функции комплексного переменного:

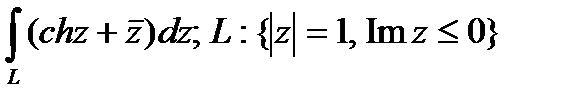
Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 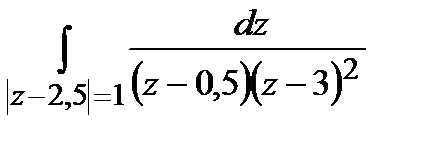; б) .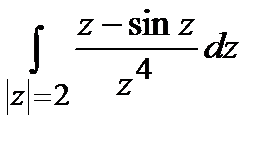

Задание 5. Вычислить интегралы с помощью вычетов.

1.

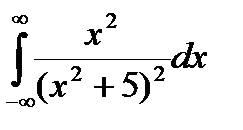
2.

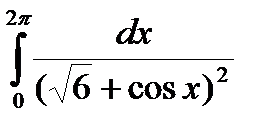
Вариант №15

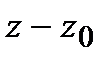Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

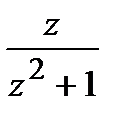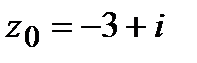Задание 2. Для функции 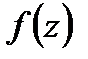найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

= ;

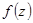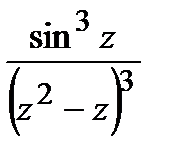З адание 3. В ычислить интеграл от функции комплексного переменного:

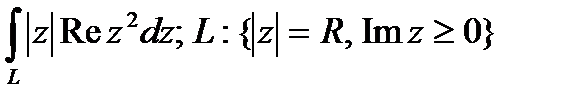
Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 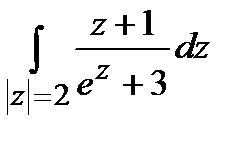; б) .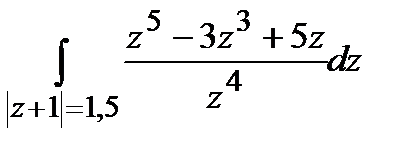

Задание 5. Вычислить интегралы с помощью вычетов.

1.

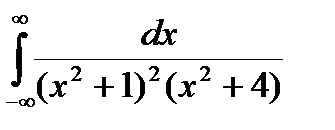
2.

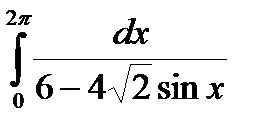
Вариант №16

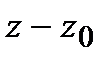Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= ,

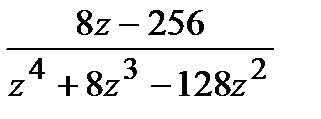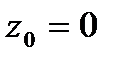
Задание 2. Для функции 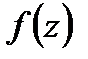найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

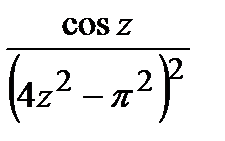
Задание 3. В ычислить интеграл от функции комплексного переменного:

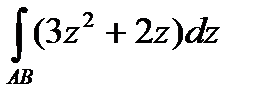
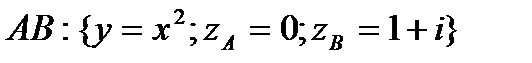
Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 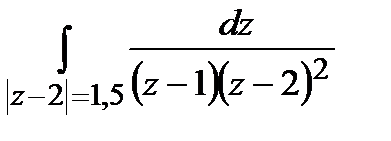; б) .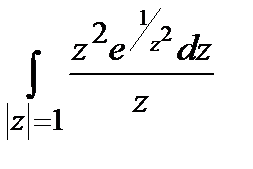

Задание 5. Вычислить интегралы с помощью вычетов.

1.

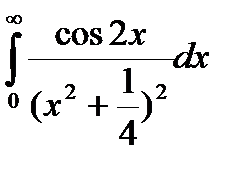
2.

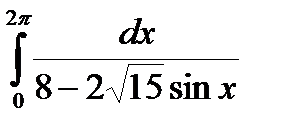
Вариант №17

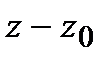Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

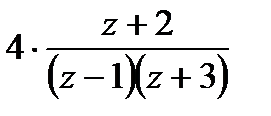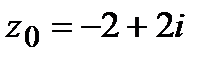Задание 2. Для функции 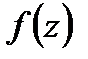найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

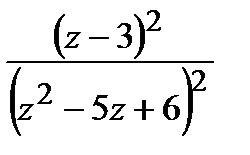
Задание 3. В ычислить интеграл от функции комплексного переменного:

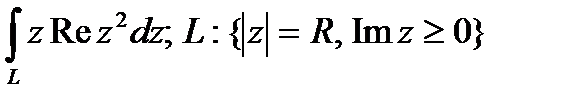
Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 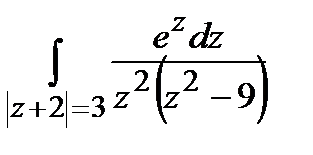; б) .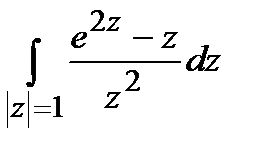

Задание 5. Вычислить интегралы с помощью вычетов.

1.

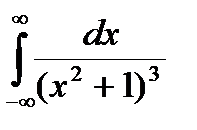
2.

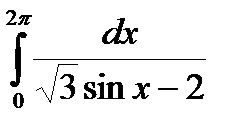
Вариант №18

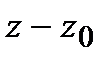Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= ,

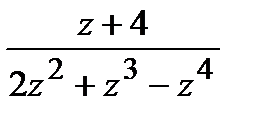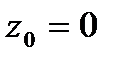
Задание 2. Для функции 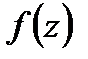найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

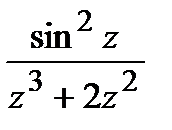
Задание 3. В ычислить интеграл от функции комплексного переменного:

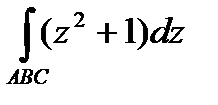; АВС – ломаная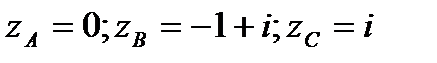

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 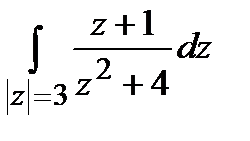; б) .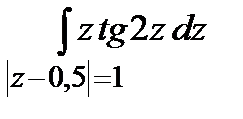

Задание 5. Вычислить интегралы с помощью вычетов.

1.

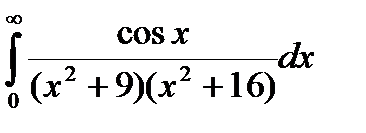
2.

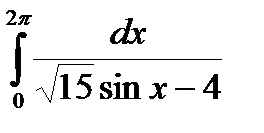
Вариант №19

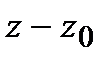Задание 1. Найти все лорановские разложения данной функции по степеням . Указать главную и правильную части ряда.

= , .

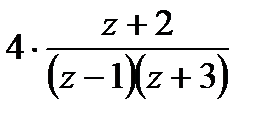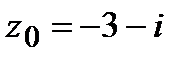Задание 2. Для функции 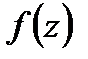найти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

=

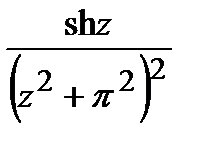
Задание 3. В ычислить интеграл от функции комплексного переменного:

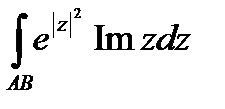; АВ – отрезок прямой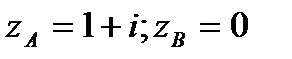

Задание 4. Вычислить интегралы, используя теорему Коши о вычетах.

а) 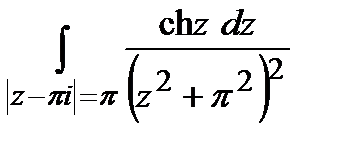; б) .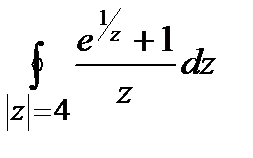

Задание 5. Вычислить интегралы с помощью вычетов.

1.

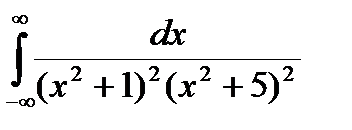
2.

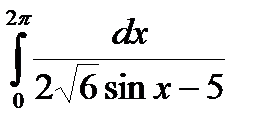
Вариант №20