Задание 1

Физико-математический факультет

Кафедра математики
и экономико-математических методов

СПЕЦИАЛЬНЫЕ
РАЗДЕЛЫ МАТЕМАТИКИ

Методическое пособие

Тирасполь, 2015

УДК 51 (072)

ББК В1р30

И 6О

Составители:

Л.В. Елкина, ст. преп.

Рецензенты:

Л.В. Чуйко, канд.пед. наук, доцент кафедры М и ЭММ, физико-математического факультета.

В.В. Звонкий, канд. тех. наук, доцент кафедры, инженерно технического факультета.

Специальные разделы математики: методическое пособиеI/ Сост.: Елкина Л.В. – Тирасполь, 2015. – 173 с.

Методическое пособие по дисциплине «Специальные разделы математики» предназначено для дополнительного и углубленного изучения данного курса. Содержит варианты для индивидуальных работ, предусмотренных по этой дисциплине.

Работа составлена в соответствии с требованиями Федерального Государственного образовательного стандарта ВПО третьего поколения по направлению 151701.65 «Проектирование технологических машин и комплексов», 151000 «Технологические машины и оборудование», утвержденного приказом Министерства образования и науки Российской Федерации от 09 ноября 2009 г. № 533.

Адресуется студентам инженерных специальностей.

УДК 51 (072)

ББК В1р30 Рекомендовано Научно-методическим советом ПГУ им.Т.Г.Шевченко

© Составители: Елкина Л.В., 2015

ПРЕДИСЛОВИЕ

Методическое пособие по дисциплине «Специальные разделы математики», включает в себя 20 вариантов индивидуальных заданий по четырем основным темам: Криволинейные и повторные интегралы, теория поля, функции комплексного переменного и элементы операционного исчисления, список вопросов для подготовки к зачету, а также список необходимой литературы.

Методическое пособие составлено в соответствии с учебным планом и рабочей программой дисциплины. Количество вариантов исключает переписывание одного и того же варианта, а решенные примеры в сочетании с другими пособиями по данному курсу окажет большую помощь студентам-бакалаврам дневного и заочного отделений в их самостоятельной работе, как при выполнении индивидуальных, контрольных работ, так и при подготовке к зачету.

Задание для индивидуальных работ:

Индивидуальная работа №1

Вариант 1

1. Вычислить криволинейный интеграл первого рода 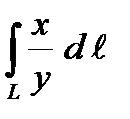, если L – дуга окружности .

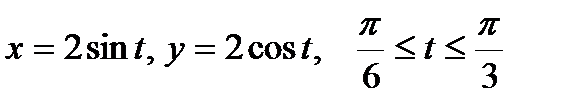2. Вычислить криволинейный интеграл второго рода 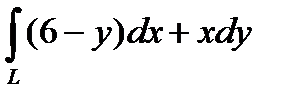, где L – арка циклоиды .

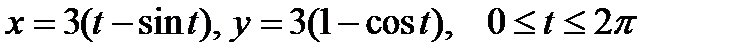3. Вычислить поверхностный интеграл первого рода 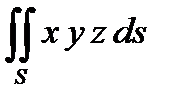по пространственной области 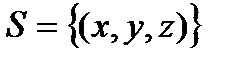, определяемой условиями .

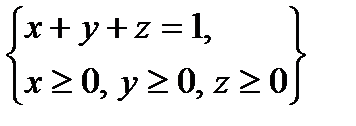4. Вычислить по формуле Стокса криволинейный интеграл 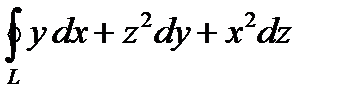, где L – окружность, по которой плоскость 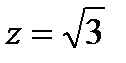пересекает сферу, заданную уравнением .

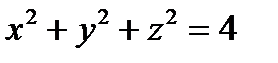Вариант 2

1. Вычислить криволинейный интеграл первого рода 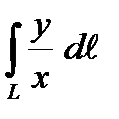по кривой L .

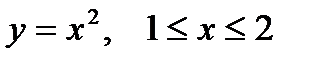2. Вычислить криволинейный интеграл второго рода 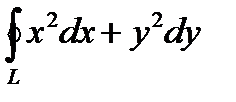, если L – контур эллипса 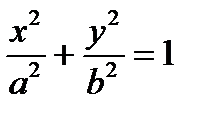, взятый при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 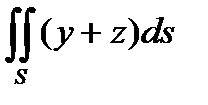по пространственной области 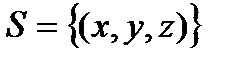, определяемой условиями .

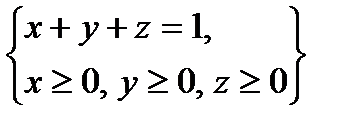4. Вычислить поверхностный интеграл второго рода 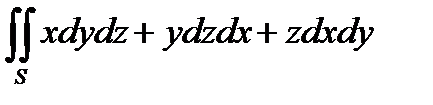, где S - внешняя сторона сферы .

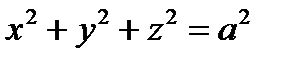Вариант 3

1. Вычислить криволинейный интеграл первого рода 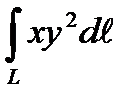по кривой L: .
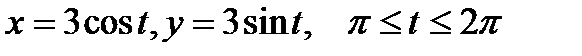2. Вычислить криволинейный интеграл второго рода 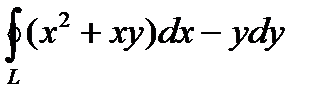, L-контур квадрата АВСD с вершинами А(1,0), В(0,1), С(-1,0), D(0,-1), взятый при положительном направлении обхода.
3. Вычислить поверхностный интеграл первого рода 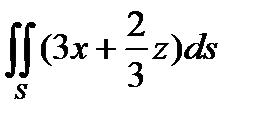по пространственной области 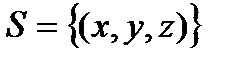, определяемой условиями .
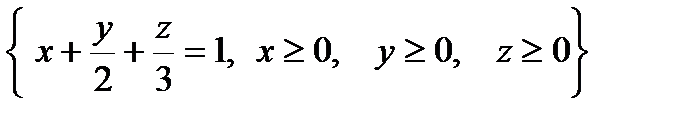4. Вычислить поверхностный интеграл II рода 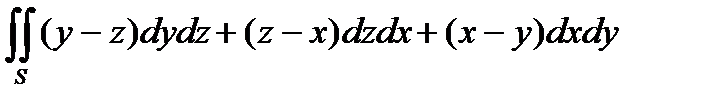, где S - нижняя сторона части конической поверхности 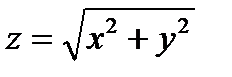, при .

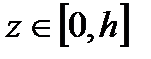Вариант 4

1. Вычислить криволинейный интеграл первого рода 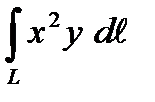по кривой L: .

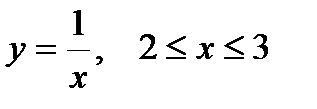2. Вычислить криволинейный интеграл второго рода 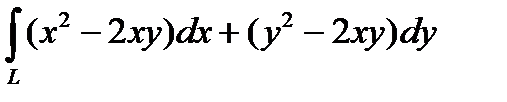, где L - дуга параболы 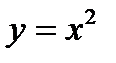при 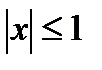при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 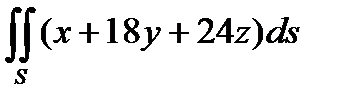по пространственной области 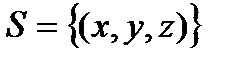, определяемой условиями .

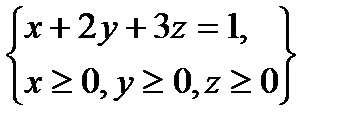4. Вычислить поверхностный интеграл II рода 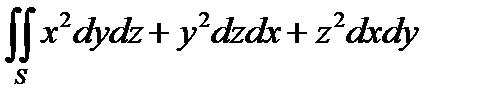, где S - внешняя сторона сферы 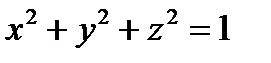при .

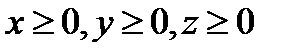Вариант 5

1. Вычислить криволинейный интеграл первого рода 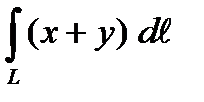по кривой L: .

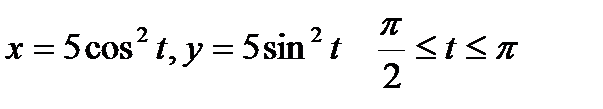2. Вычислить криволинейный интеграл второго рода 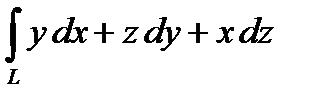, L - отрезок прямой АВ, А(0,1,2), В(3,2,-1).

3. Вычислить поверхностный интеграл первого рода 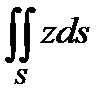по пространственной области 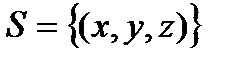, определяемой условиями .

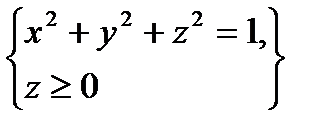4. Пользуясь формулой Стокса, вычислить криволинейный интеграл 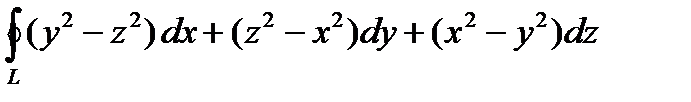, где L – граница сечения куба 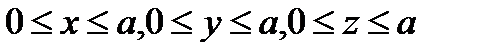плоскостью 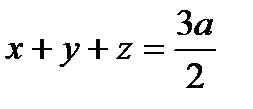, которая обходится против часовой стрелки, если смотреть из точки (2 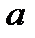,0,0).

Вариант 6

1. Вычислить криволинейный интеграл первого рода 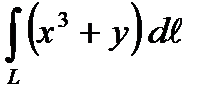по кривой L: .

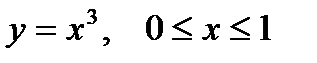2. Вычислить криволинейный интеграл второго рода 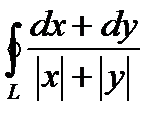, L-контур квадрата АВСD с вершинами А(1,0), В(0,1), С(-1,0), D(0,-1), взятый при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 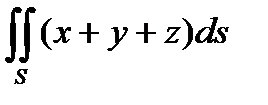по пространственной области 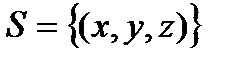, определяемой условиями .

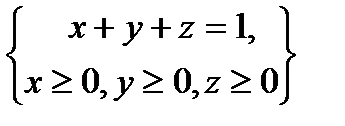4. С помощью формулы Остроградского-Гаусса вычислить поверхностный интеграл II рода 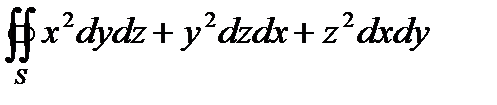по внешней стороне S сферы .

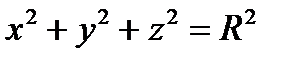Вариант 7

1. Вычислить криволинейный интеграл первого рода 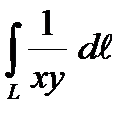по дуге астроиды L: .

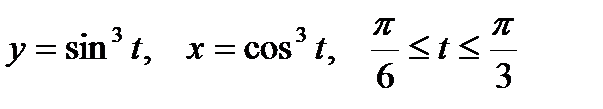2. Вычислить криволинейный интеграл второго рода 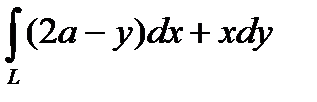, где L – арка циклоиды 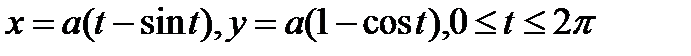при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 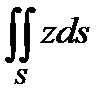по пространственной области 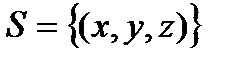, определяемой условиями .

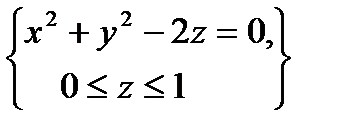4. Вычислить поверхностный интеграл II рода 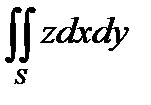, где S - нижняя сторона части конуса 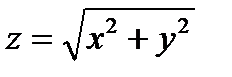, заключенного между плоскостям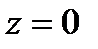и и .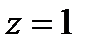

Вариант 8

1. Вычислить криволинейный интеграл первого рода 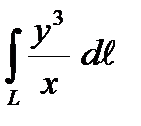по кривой L: .

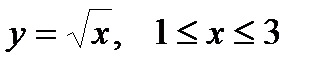2. Вычислить криволинейный интеграл второго рода 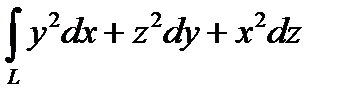, где L – часть кривой Вивиани 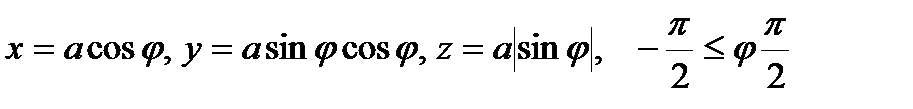при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 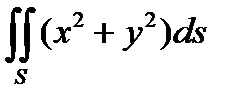по пространственной области 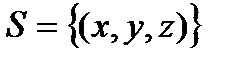, определяемой условиями .

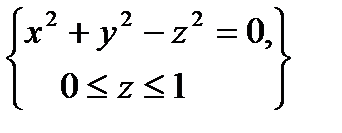4. Вычислить поверхностный интеграл II рода 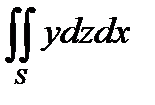, где S - верхняя сторона параболоида 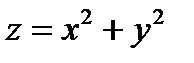, заключенного между плоскостям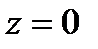и и .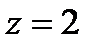

Вариант 9

1. Вычислить криволинейный интеграл первого рода 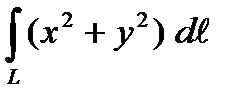по дуге циклоиды L: .

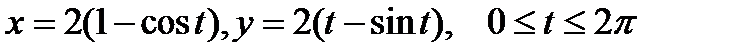2. Вычислить криволинейный интеграл второго рода 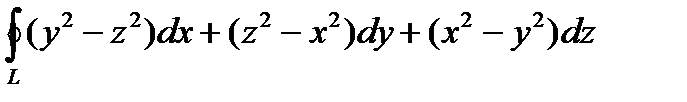, где L – контур, образованный линиями пересечения сферы 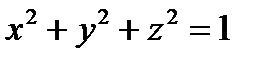с координатными плоскостями, 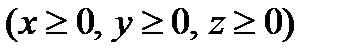при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 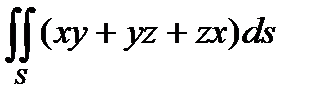по пространственной области 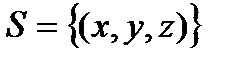, определяемой условиями .

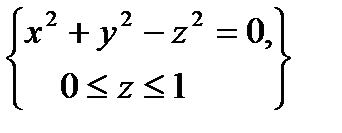4. Вычислить поверхностный интеграл II рода 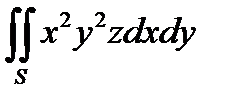по верхней стороне верхней половины сферы .

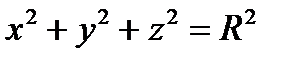Вариант 10

1. Вычислить криволинейный интеграл первого рода 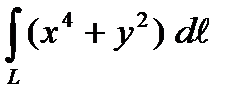по кривой L: .

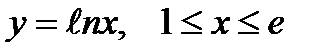2. Вычислить криволинейный интеграл второго рода 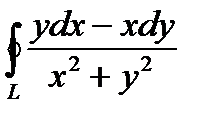, где L – дуга окружности радиуса 2 с центром в начале координат при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 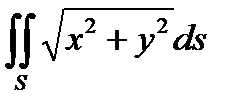по пространственной области 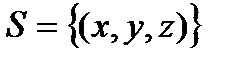, определяемой условиями .

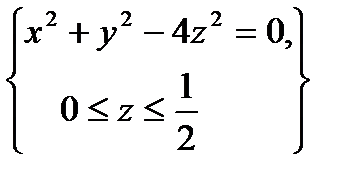4. Вычислить поверхностный интеграл второго рода 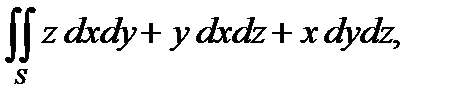где S – верхняя сторона плоскости 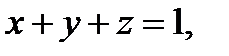ограниченной координатными плоскостями.

Вариант 11

1. Вычислить криволинейный интеграл первого рода 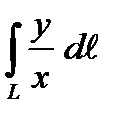по кривой L: .

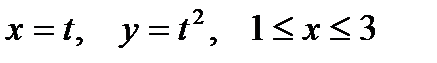2. Вычислить криволинейный интеграл второго рода 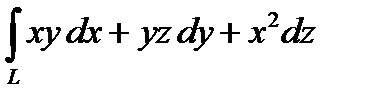, где L – дуга винтовой линии 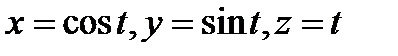от точки А (1,0,0) до точки В (1,0,2 ).

3. Вычислить поверхностный интеграл первого рода 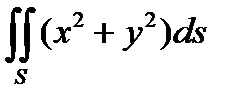по пространственной области 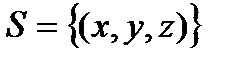, определяемой условиями .

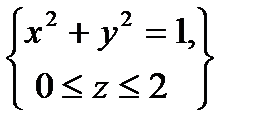4. Вычислить поверхностный интеграл второго рода 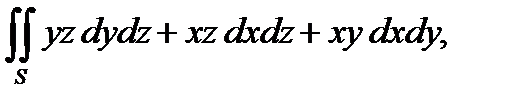где S – внешняя сторона поверхности, ограниченной плоскостями .

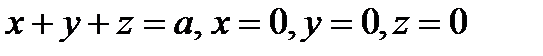Вариант 12

1. Вычислить криволинейный интеграл первого рода 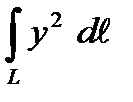по кривой L: .

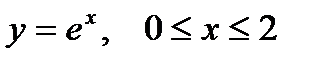2. Вычислить криволинейный интеграл второго рода 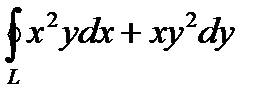, где L – дуга эллипса 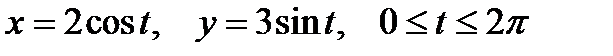при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 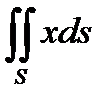по пространственной области 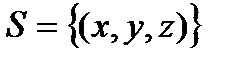, определяемой условиями .

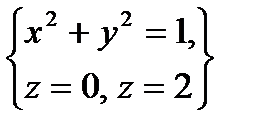4. Вычислить поверхностный интеграл второго рода 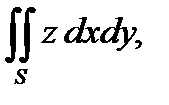где S – внешняя сторона эллипсоида .

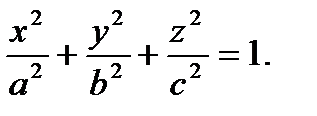Вариант 13

1. Вычислить криволинейный интеграл первого рода 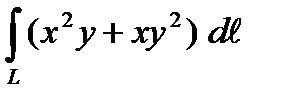по дуге L окружности 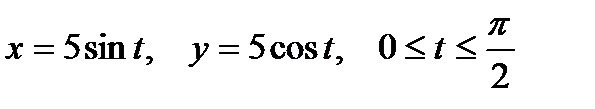, расположенной в первой координатной четверти.

2. Вычислить криволинейный интеграл второго рода 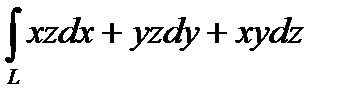, где L - дуга винтовой линии 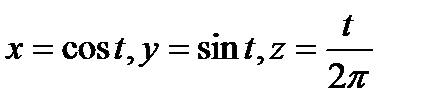от точки А(1,0,0) до точки В(1,0,1).

3. Вычислить поверхностный интеграл первого рода 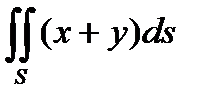по пространственной области 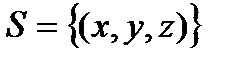, определяемой условиями .

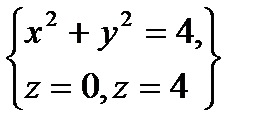4. Вычислить поверхностный интеграл второго рода 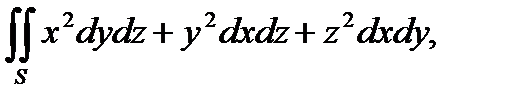где S – внешняя сторона поверхности верхней полусферы .

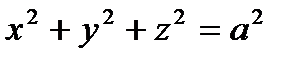Вариант 14

1. Вычислить криволинейный интеграл первого рода 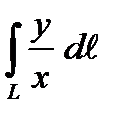, если L – дуга параболы .

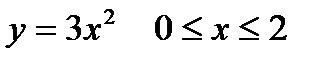2. Вычислить криволинейный интеграл второго рода 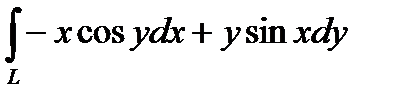, где L - отрезок прямой от точки А(0,0) до точки В .

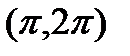3. Вычислить поверхностный интеграл первого рода 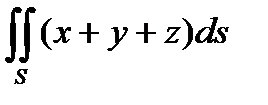по пространственной области 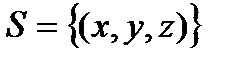, определяемой условиями .

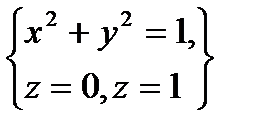4. Вычислить поверхностный интеграл второго рода 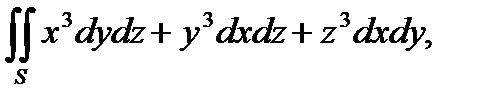где S – внешняя сторона поверхности .

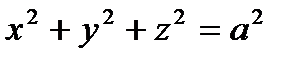Вариант 15

1. Вычислить криволинейный интеграл первого рода 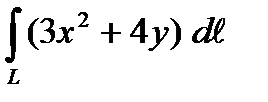, если L –дуга окружности .

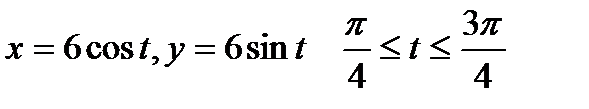2. Вычислить криволинейный интеграл второго рода 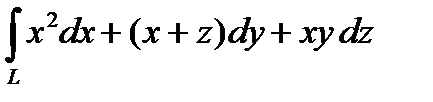, где L – дуга кривой 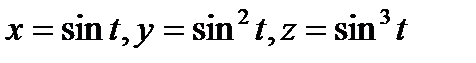при .

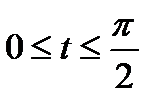3. Вычислить поверхностный интеграл первого рода 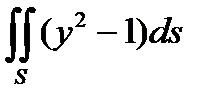по пространственной области 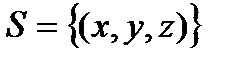, определяемой условиями .

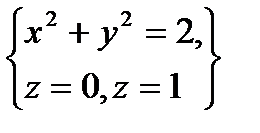4. Вычислить поверхностный интеграл второго рода 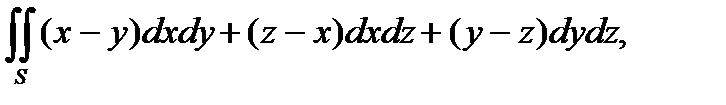где S – внешняя сторона конической поверхности .

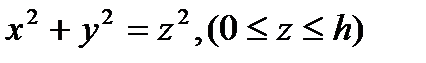Вариант 16

1. Вычислить криволинейный интеграл первого рода 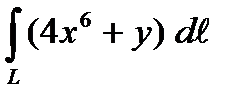, если L –дуга кривой .

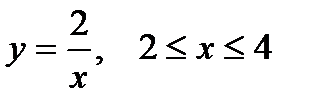2. Вычислить криволинейный интеграл второго рода 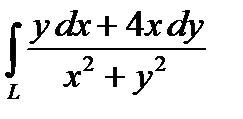, где L – отрезок прямой от точки А(1,2) до точки В(2,8).

3. Вычислить поверхностный интеграл первого рода 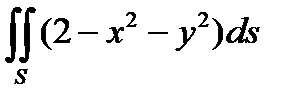по пространственной области 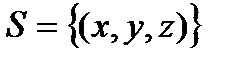, определяемой условиями .

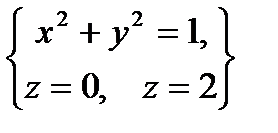4. Вычислить поверхностный интеграл второго рода 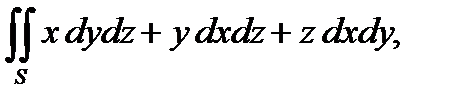где S – положительная сторона куба, составленного плоскостями .

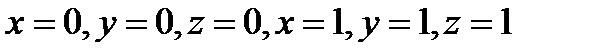Вариант 17

1. Вычислить криволинейный интеграл первого рода 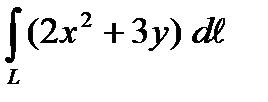, если L –дуга кривой .

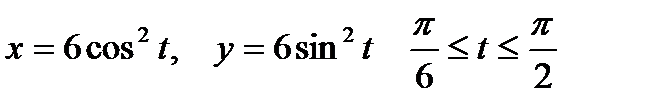2. Вычислить криволинейный интеграл второго рода 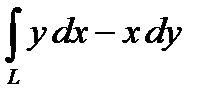, где L – дуга астроиды 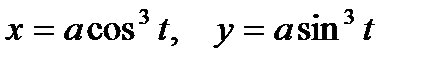от точки А(а,0) до точки В(0,а).

3. Вычислить поверхностный интеграл первого рода 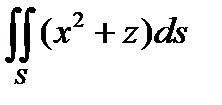по пространственной области 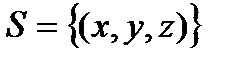, определяемой условиями .

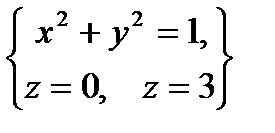4. Вычислить поверхностный интеграл второго рода 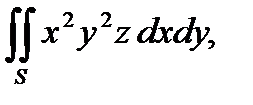где S – положительная сторона нижней половины сферы .

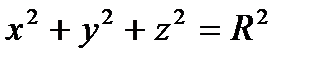Вариант 18

1. Вычислить криволинейный интеграл первого рода 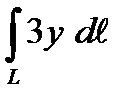, если L – дуга кубической параболы .

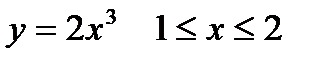2. Вычислить криволинейный интеграл второго рода 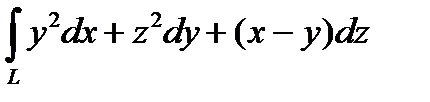, где L – отрезок прямой от точки А(1,0,2) до точки В (2,-1,0).

3. Вычислить поверхностный интеграл первого рода 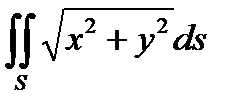по пространственной области 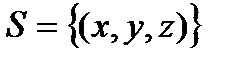, определяемой условиями .

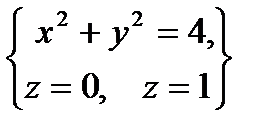4. Вычислить поверхностный интеграл второго рода 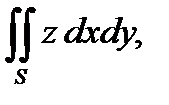где S – внешняя сторона эллипсоида .

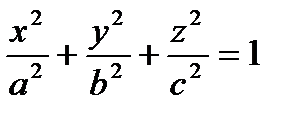Вариант 19

1. Вычислить криволинейный интеграл первого рода 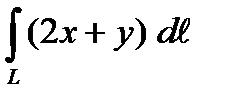, если L – дуга астроиды .

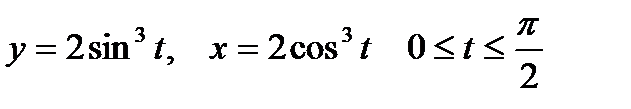2. Вычислить криволинейный интеграл второго рода 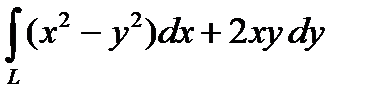, где L – дуга параболы 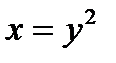при .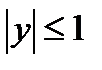

3. Вычислить поверхностный интеграл первого рода 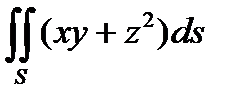по пространственной области 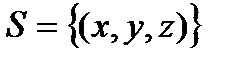, определяемой условиями .

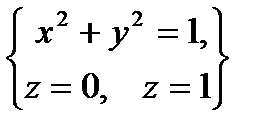4. Вычислить поверхностный интеграл второго рода 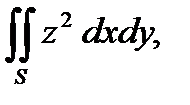где S – внешняя сторона эллипсоида .

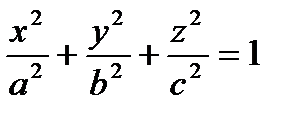Вариант 20

1. Вычислить криволинейный интеграл первого рода 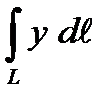, если L – дуга кривой .

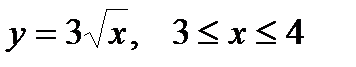2. Вычислить криволинейный интеграл второго рода 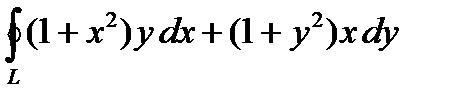, где L – контур треугольника АВС с вершинами А(0,0), В(2,0), С(4,2) при положительном направлении обхода.

3. Вычислить поверхностный интеграл первого рода 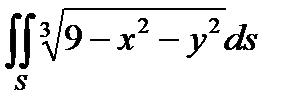по пространственной области 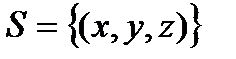, определяемой условиями .

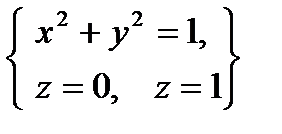4. Вычислить поверхностный интеграл второго рода 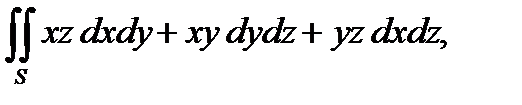где S – внешняя сторона пирамиды, составленной плоскостями 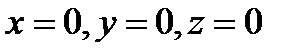и .

И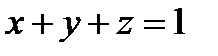ндивидуальная работа №2.

Вариант №1

Задание 1. Найти производную функции z по направлению вектора 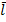в точке М ₀, gradz, 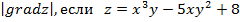, , 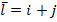М ₀ (1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

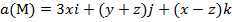, (p):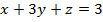

Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

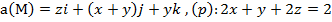Задание 4. Выяснить, является ли векторное поле 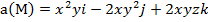соленоидальным.

Вариант №2

Задание 1. Найти производную функции z по направлению вектора 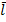в точке М ₀, gradz, 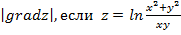, , 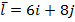М ₀ (1,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

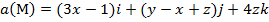, (p): .

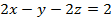Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

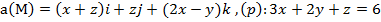Задание 4. Выяснить, является ли векторное поле 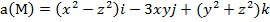соленоидальным.

Вариант №3

Задание 1. Найти производную функции u по направлению вектора 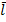в точке М ₀, gradz, 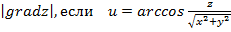, , 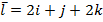М ₀ (1,1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

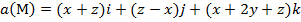, (p): .

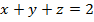Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

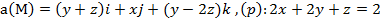Задание 4. Выяснить, является ли векторное поле 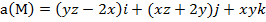соленоидальным.

Вариант №4

Задание 1. Найти gradz, 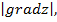производную функции 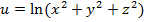по направлению вектора 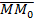в точке М ₀(1,2,1), если М(3,6,5).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

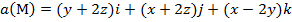, (p): .

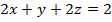Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

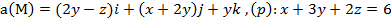Задание 4. Выяснить, является ли векторное поле 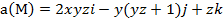соленоидальным.

Вариант №5

Задание 1. Найти производную функции z по направлению вектора 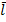в точке М ₀, gradz,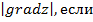 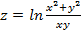, , 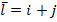М ₀ (1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

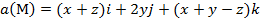, (p): .

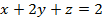Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

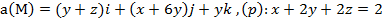Задание 4. Выяснить, является ли векторное поле 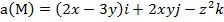соленоидальным.

Вариант №6

Задание 1. Найти производную функции z по направлению вектора 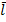в точке М ₀, gradz,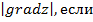 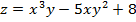, , 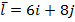М ₀ (1,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

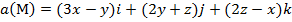, (p): .

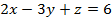Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

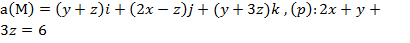Задание 4. Выяснить, является ли векторное поле 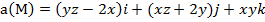потенциальным.

Вариант №7

Задание 1. Найти производную функции u по направлению вектора 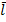в точке М ₀, gradz,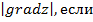 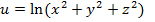, , 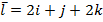М ₀ (1,1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

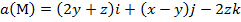, (p): .

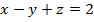Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

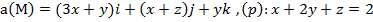Задание 4. Выяснить, является ли векторное поле 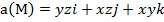потенциальным.

Вариант №8

Задание 1. Найти gradz, 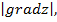производную функции 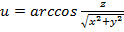по направлению вектора 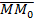в точке М ₀(1,2,1), если М(3,6,5).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

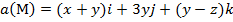, (p): .

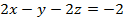Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

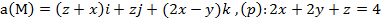Задание 4. Выяснить, является ли векторное поле 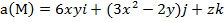потенциальным.

Вариант №9

Задание 1. Найти производную функции z по направлению вектора 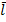в точке М ₀, gradz,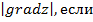 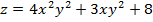, , 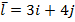М ₀ (1,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

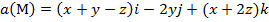, (p): .

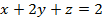Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

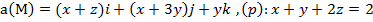Задание 4. Выяснить, является ли векторное поле 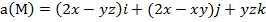потенциальным.

Вариант №10

Задание 1. Найти производную функции z по направлению вектора в точке М ₀, gradz, 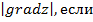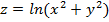, , 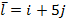М ₀ (3,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

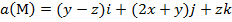, (p): .

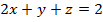Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

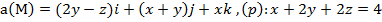Задание 4. Выяснить, является ли векторное поле 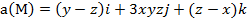потенциальным.

Вариант №11

Задание 1. Найти производную функции u по направлению вектора 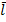в точке М ₀, gradz, 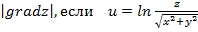, , 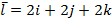М ₀ (1,3,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

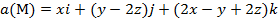, (p): .

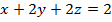Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

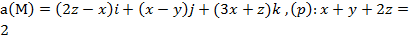Задание 4. Выяснить, является ли векторное поле 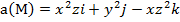гармоническим.

Вариант №12

Задание 1. Найти gradz, 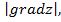производную функции 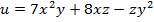по направлению вектора 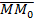в точке М ₀(1,2,1), если М(2,3,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

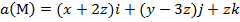, (p): .

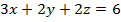Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

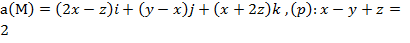Задание 4. Выяснить, является ли векторное поле 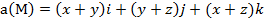гармоническим.

Вариант №13

Задание 1. Найти производную функции z по направлению вектора 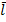в точке М ₀, gradz,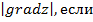 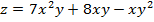, , 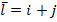М ₀ (1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

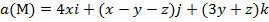, (p): .

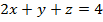Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

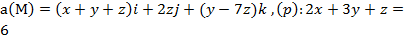Задание 4. Выяснить, является ли векторное поле 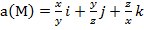гармоническим.

Вариант №14

Задание 1. Найти производную функции z по направлению вектора 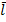в точке М ₀, gradz, 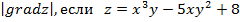, , 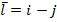М ₀ (2, ).

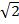Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

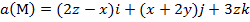, (p): .

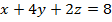Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

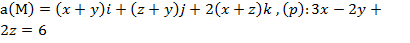Задание 4. Выяснить, является ли векторное поле 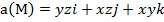гармоническим.

Вариант №15

Задание 1. Найти производную функции u по направлению вектора 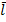в точке М ₀, gradz,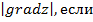 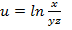, , 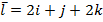М ₀ (1,3,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

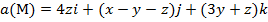, (p): .

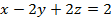Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

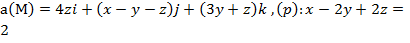Задание 4. Выяснить, является ли векторное поле 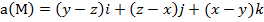гармоническим.

Вариант №16

Задание 1. Найти, gradz, 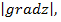производную функции 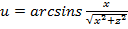по направлению вектора 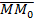в точке М ₀(1,2,1), если М(3,6,5).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

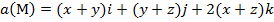, (p): .

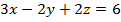Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

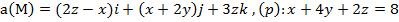Задание 4. Выяснить, является ли векторное поле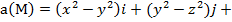

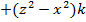соленоидальным.

Вариант №17

Задание 1. Найти производную функции z по направлению вектора 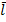в точке М ₀, gradz, 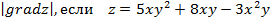, , 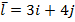М ₀ (1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

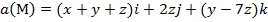, (p): .

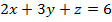Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

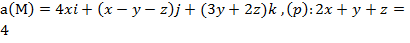Задание 4. Выяснить, является ли векторное поле 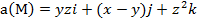соленоидальным.

Вариант №18

Задание 1. Найти производную функции z по направлению вектора 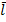в точке М ₀, gradz, 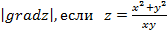, , 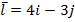М ₀ (1,2).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

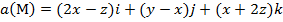, (p): .

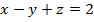Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

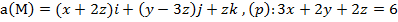Задание 4. Выяснить, является ли векторное поле 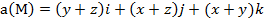соленоидальным.

Вариант №19

Задание 1. Найти производную функции u по направлению вектора 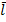в точке М ₀

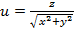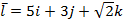, , М ₀ (1,1,1).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

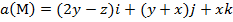, (p): .

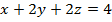Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

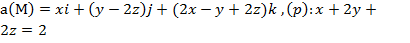Задание 4. Выяснить, является ли векторное поле 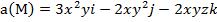соленоидальным.

Вариант №20

Задание 1. Найти производную функции 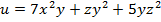по направлению вектора 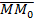в точке М ₀(1,2,1), если М(3,6,5).

Задание 2. Вычислить поток векторного поля а(М) через верхнюю поверхность пирамиды, образуемой плоскостью (р) и координатными плоскостями, двумя способами: 1) использовав определение потока;

2) с помощью формулы Остроградского –Гаусса.

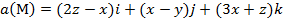, (p): .

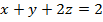Задание 3. Вычислить циркуляцию векторного поля а(М) по контуру треугольника, полученного в результате пересечения плоскости (р) с координатными плоскостями, при положительном направлении обхода относительно нормального вектора n(A,B,C) этой плоскости двумя способами:1) использовав определение циркуляции;

2) с помощью формулы Стокса

.

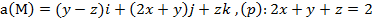Задание 4. Выяснить, является ли векторное поле 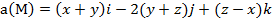соленоидальным.

Индивидуальная работа №3.

Вариант №1

Задание 1.

а) Найти модуль и аргумент чисел 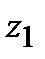= 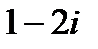и 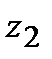= 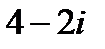. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , , .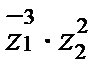

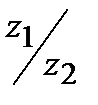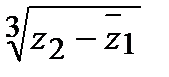Задание 2. Вычислить значение функции 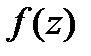в точке 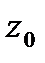, ответ представить в алгебраической форме комплексного числа:

а) 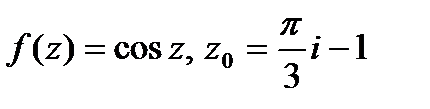; б) .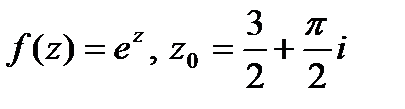

Задание 3. Указать область дифференцируемости функции 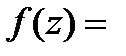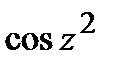и вычислить производную. Выделить действительную и мнимую часть полученной производной.

Вариант №2