2015-04-12
439
а) Найти модуль и аргумент чисел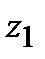 
= 
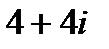и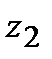 
= 
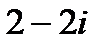. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.
б) Найти: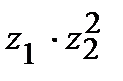 
, 
, 
.
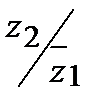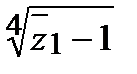Задание 2. Вычислить значение функции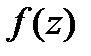 
в точке 
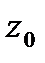, ответ представить в алгебраической форме комплексного числа:
а)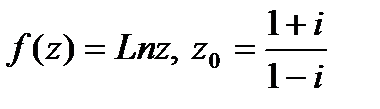 
; б)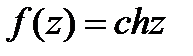 
, 
.
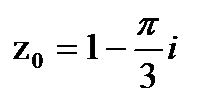Задание 3. Указать область дифференцируемости функции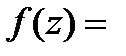 
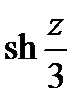и вычислить производную. Выделить действительную и мнимую часть полученной производной.
Вариант №3
