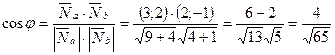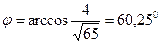Решение. Так как (а) || ( в) тогда и только тогда, когда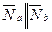

; .

Так как (а) || ( в) тогда и только тогда, когда , то

равенство 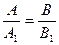является признаком параллельности прямых.

Так как (а) 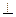(в) тогда и только тогда, когда ,

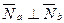то равенство АА₁ + ВВ₁ = 0 является признаком перпендикулярности прямых.

Угол между прямыми можно выразить через их угловые

коэффициенты.

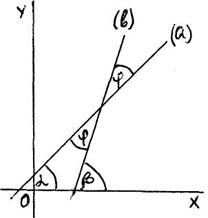
Пусть 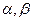- углы, которые составляют прямые (а) и (в) с осью ох соответственно. Тогда угол 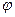между прямыми (a) и (в) равен 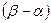. Следовательно,

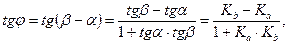
где К_а, К_в – угловые коэффициенты прямых (а) и (в).

Пример. Вычислить угол 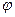между прямыми (а) и (в) по их уравнениям: у = Зх + 5, 5х + 2у = 4.

Решение. Так как К _а = 3, К_в = 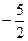, то , .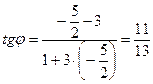

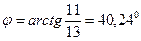Так как параллельные прямые пересекают ось ох под одинаковым углом, то равенство К_{а =} К_в является условием параллельности прямых (а) и (b).

Так как дробь 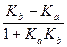не существует, когда 1 + К_аК_в = 0,

то равенство К_в= 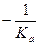является условием перпендикулярности прямых (а) и (в).