2015-04-12
1772
Статистические оценки случайной величины (выборочное среднее, выборочная дисперсия и т.д.)могут служить только приближением соответствующих характеристик генеральной совокупности. При этом эти оценки должны удовлетворять определённым требованиям.
Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического (истинного) распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема п и вычислим для каждой из них оценку параметра Θ:
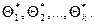
Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения 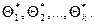Если математическое ожидание Θ* не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если М (Θ*) >Θ, и с недостатком, если М (Θ*) < Θ). Следовательно, необходимым условием отсутствия систематических ошибок является требование
М(Θ*) = Θ. (35.1)
Если требование (35.1) выполняется, то есть математическое ожидание оценки равно оцениваемому параметру, то статистическая оценка Θ* называется несмещенной.
Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию.
Состоятельной называется статистическая оценка, которая при п →∞ стремится по вероятности к оцениваемому параметру.
Дополнение. Говорят, что бесконечная последовательность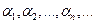 
стремится по вероятности к 
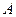при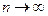 
, если для любого 
:
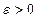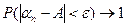, когда 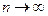. (35.1)
Выборочное среднее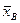 
представляет собой несмещенную оценку математического ожидания М (Х).
Действительно, будем рассматривать 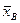как случайную величину, а х 1, х 2,…, хп, то есть значения исследуемой случайной величины, составляющие выборку,– как независимые, одинаково распределенные случайные величины Х 1, Х 2,…, Хп, имеющие математическое ожидание а. Из свойств математического ожидания следует, что
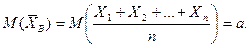
Но, поскольку каждая из величин Х 1, Х 2,…, Хп имеет такое же распределение, что и генеральная совокупность, а = М (Х), то есть М (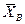
) = М (Х), что и требовалось доказать.
Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания.
В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Можно доказать, что
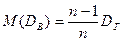, (35.2)
где DГ – истинное значение дисперсии генеральной совокупности. Можно предложить другую оценку дисперсии – исправленную дисперсию s ², вычисляемую по формуле
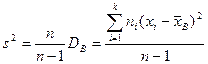. (35.3)
Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение
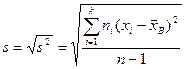. (35.4)
