2015-04-12
2299
Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего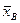 
оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 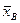как случайную величину 
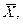а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х 1, Х 2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом
, 
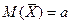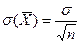(38.1)
(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства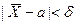 
. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
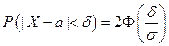. (38.2)
Тогда, с учетом того, что ,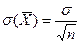
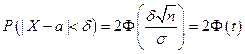, (38.3)
где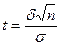 
. Отсюда 
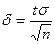, и предыдущее равенство можно переписать так:
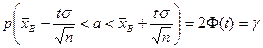. (38.4)
Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал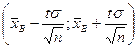 
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
|
|
|
Пример. Найдем доверительный интервал для математического ожидания нормально распределенной случайной величины, если объем выборки п = 49,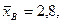 
σ = 1,4, а доверительная вероятность γ = 0,9.
Определим t, при котором Ф(t) = 0,9:2 = 0,45: t = 1,645. Тогда
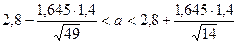, или 2,471 < a < 3,129.
Найден доверительный интервал, в который попадает а с надежностью 0,9.
