Тензоры

Тензоры возникли как естественное развитие представлений об объектах линейной алгебры: если скаляр в 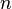-мерном представляется нульмерным объектом (состоящим только из одного элемента поля), вектор — одномерным массивом (матрицей размера 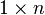), линейное преобразование — двумерной матрицей, то тензор может быть представлен как многомерный массив элементов поля размера 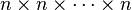(количество измерений массива называют валентностью тензора), а скаляры, векторы, линейные операторы оказываются частными случаями тензора (с валентностями 0, 1 и 2 соответственно). Следующее обобщение, использованное в понятии тензора взято из возможности представления линейного функционала как ковектора и идея двойственности между пространством и егосопряжением — пространством его линейных функционалов; используя эту возможность, тензор валентности рассматривается как 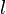раз контравариантный, то есть, рассматриваемый соответствующими компонентами в «обычном» базисе, и 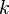раз ковариантный, то есть, с компонентами в сопряжённом пространстве (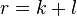, «тензор ранга »).

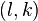В тензорной алгебре вводятся и изучаются линейные операции над тензорами, такие, как умножение на скаляр, сложение, свёртка. Особую роль играет операциятензорного произведения (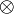), обобщение которой на линейные пространства позволило обобщить и определение тензора: рассматривать тензор ранга 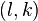в линейном пространстве 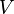как элемент тензорного произведения 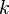экземпляров 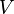и 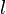экземпляров сопряжённого ему :

.

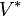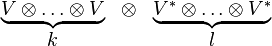Квадратичные и билинейные формы [править | править вики-текст]

Основные статьи: Квадратичная форма, Билинейная форма

Алгебраические формы (однородные многочлены на векторных пространствах, задаваемые однородными многочленами от координат вектора) относятся кполилинейной алгебре, но квадратичные, билинейные формы, и некоторые специальные виды форм (полуторалинейные, эрмитовы) важны также в чисто линейной алгебре. Значение билинейных и квадратичных форм заключается в том, что они выражаются матрицами, как и линейные операторы. Наиболее детально изучены свойства симметричных 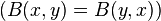и кососимметричных 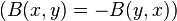билинейных форм.