Пример 2. Закодируем буквы алфавита из примера 1 в коде Шеннона-Фано.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)
Таблица 4.1.
| X | P | Коды | ||||
| x1 | 1/4 | ------- | ------- | |||
| x2 | 1/4 | ------- | ------- | |||
| x3, | 1/8 | ------- | ||||
| x4 | 1/8 | ------- | ||||
| x5 | 1/16 | |||||
| x6 | 1/16 | |||||
| x7 | 1/16 | |||||
| x8 | 1/16 |
Средняя длина полученного кода будет равна
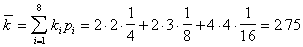
Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы.
Пример 3.
Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице 4.2.
Таблица 4.2.
| Буква | Рi | Код | ||||
| ب | 0.145 | - | ||||
| о | 0.095 | - | ||||
| е | 0.074 | |||||
| а | 0.064 | |||||
| и | 0.064 | |||||
| н | 0.056 | |||||
| т | 0.056 | … | … | - | ||
| с | 0.047 | … | … | |||
| ... | … | |||||
| ф | 0.03 |
Средняя длина данного кода будет равна, 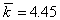 бит/букву;
бит/букву;
Энтропия H=4.42 бит/буква. Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины 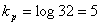 , то эффективность была бы значительно ниже.
, то эффективность была бы значительно ниже. 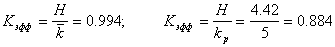
 2015-04-17
2015-04-17 605
605








