2015-04-01
648
Построенные оценки параметров уравнения регрессии являются точечтными оценками. Доверительные интервалы для парметров уравнения регрессии являются их интервальными оценками.
100(1-a)% -ный доверительный интервал для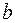 
:
 ,
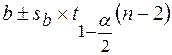| (49) |
100(1-a)% - ный доверительный интервал для a:
 .
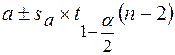| (50) |
Статистика t1-a/2(n-2) имеет распределение Стьюдента с (n-2) степенями свободы.
Если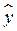 
интерпретируется как наилучшая оценка единственного значения y, соответствующего х = хi (см. (42)), а также число наблюдений достаточно велико (по крайней мере, больше 30), то для 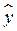может быть построен, так называемый, «быстрый» доверительный интервал.
100(1-a)% - ный доверительный интервал для :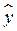
 .
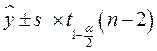| (51) |
где s – стандартная ошибка оценки.
Таблица дисперсионного анализа для простой линейной регрессии
Дисперсию оценки можно также найти из таблицы дисперсионного анализа, которую можно получить стандартными средствами в большинстве систем обработки статистических данных (табл. 2).
Величина s2 идентична среднему квадрату отклонения (остатка) от регрессии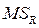 
. Она вычисляется как отношение остаточной суммы квадратов 
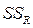к остаточному числу степеней свободы 
.
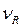Таблица 2 – Таблица дисперсионного анализа для простой линейной регрессии
| Источник дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат | F-отношение |
| Регрессия |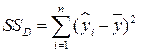 
| 
| 
| 
|
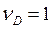
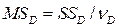
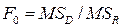
| Отклонение от регрессии |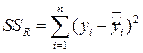 
| 
| 
| - |
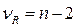
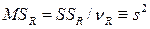
| Полная дисперсия |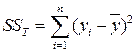 
| 
| - | - |
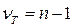
Обусловленная регрессией сумма квадратов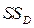 
получила такое название потому, что ее можно выразить через оценку коэффициента регрессии:
 .
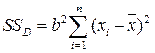| (52) |
Итак, чем больше коэффициент регрессии, тем больше сумма квадратов, «обусловленная регрессией».
Последняя колонка таблицы, называемая F -отношение, может быть использована для проверки гипотез, если ошибки предполагаются нормально распределенными.
Для проверки гипотезы о том, что простая линейная регрессия y по x отсутствует, то есть гипотезы Н0: β=0 против альтернативной гипотезы Н1: β≠0, мы используем F -отношение из таблицы дисперсионного анализа:
 .
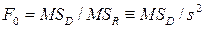| (53) |
Если верна нулевая гипотеза, то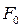 
имеет F -распределение с 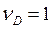и 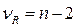степенями свободы. Соответствующее критической области р -значение вычисляется стандартными средствами обработки статистических данных автоматически.
Мы отвергаем нулевую гипотезу, если р -значение меньше, чем уровень значимости a. В этом случае мы говорим о том, что регрессионная зависимость существует.
