Пусть 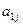 - нормативная трудоемкость изготовления одного изделия j-го типа (чел.-час);
- нормативная трудоемкость изготовления одного изделия j-го типа (чел.-час);
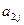 – нормативная металлоемкость одного изделия j-го типа (кг);
– нормативная металлоемкость одного изделия j-го типа (кг);
в1 – суммарная трудоемкость производственной программы предприятия (чел.-час);
в2 – суммарная металлоемкость производственной программы предприятия (кг);
Сj – отпускная цена одного изделия j- го типа (руб.);
Хj – объем производства (количество) изделий j-го типа (шт.);
j = 1, 2, 3.
Необходимо определить оптимальную производственную программу предприятия Х0 = (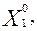
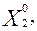
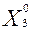 ), т.е. такое распределение объемов производства Х = (
), т.е. такое распределение объемов производства Х = (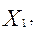
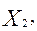
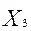 ), при котором достигается наибольший доход:
), при котором достигается наибольший доход:
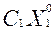 +
+ 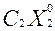 +
+ 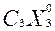 = max (
= max (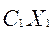 +
+ 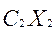 +
+ 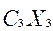 ),
),
(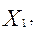
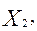
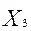 ).
).
При ограничениях на трудоемкость и металлоемкость:
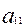
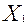 +
+ 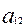
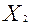 +
+ 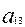
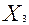 =
= 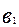 ;
;
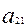
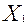 +
+ 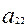
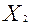 +
+ 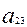
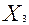 =
= 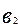 .
.
В настоящей работе мы будем предполагать следующее:
- нормы трудоемкости и металлоемкости строго положительны:
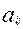 > 0; i = 1,2; j = 1,2,3;
> 0; i = 1,2; j = 1,2,3;
- объемы производства неотрицательны 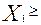 0,
0, 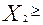 0,
0, 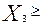 0, так что если
0, так что если 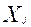 = 0, то изделие j-го типа не включается в производственную программу, i = 1, 2, 3;
= 0, то изделие j-го типа не включается в производственную программу, i = 1, 2, 3;
- оптимальная производственная программа (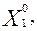
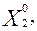
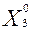 ), где
), где 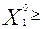 0,
0, 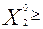 0,
0, 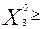 0 существует, т.е. ограничения трудоемкости и металлоемкости сбалансированы;
0 существует, т.е. ограничения трудоемкости и металлоемкости сбалансированы;
- ограничения по трудоемкости и металлоемкости независимы в том смысле, что линейно независима любая пара из векторов (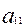 ,
, 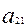 ), (
), (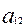 ,
, 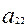 ), (
), (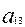 ,
, 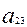 ).
).
 2015-04-17
2015-04-17 209
209








