2015-04-17
254
Пусть нормы трудоемкости изготовления трех изделий имеют значения:
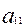= 0,2 (чел.-час); 
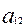= 0,8 (чел.-час); 
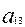= 0,4 (чел.-час),
а нормы металлоемкости тех же изделий – значения:
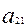= 5 (кг); 
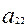= 0,8 (кг); 
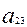= 2 (кг).
Суммарная трудоемкость производственной программы определяется величиной
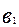= 8800 (чел.-час),
а суммарная металлоемкость –
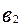= 28000 (кг).
Изделия отпускаются с предприятия по ценам за штуку:
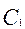= 3000 (руб); 
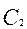= 2400 (руб); 
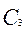= 2600 (руб).
Задача оптимизации производственной программы предприятия может быть сформулирована следующим образом: указать производственную программу (распределение объемов производства изделий) (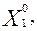
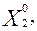
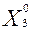), при выполнении которой достигается наибольшее значение дохода предприятия:
y = 3000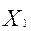 
+ 2400 
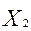+ 2600 
;
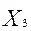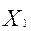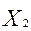0,2 + 0,8 + 0,4 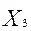= 8800;
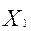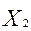5 + 0,8 + 2 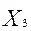= 28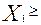00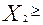0;
0,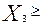 
0, 
0.
В пространстве переменных (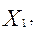
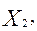
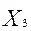) первое из ограничений (по трудоемкости) определяет плоскость 
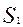, проходящую через точки:
(
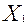= 8800/0,2 = 44000, 
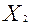= 0, 
= 0)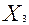 
;
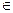
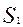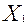( = 0, 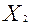= 8800/0,8 = 11000, 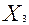= 0) ;
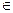
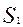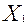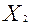( = 0, = 0, 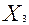= 8800/0,4 = 22000) .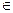
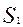Графическое изображение этой плоскости приведено на рис. 1.
Второе ограничение (по металлоемкости) определяет плоскость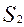 
, проходящую через точки:
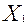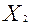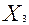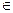
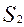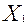( = 28000/5 = 5600, = 0, = 0) ;
( = 0, 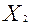= 28000/0,8 = 35000, 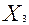= 0) ;
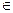
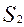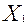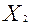( = 0, = 0, 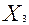= 28000/2 = 14000) .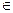
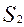Плоскость 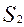также изображена на рис. 1.
Из графического изображения плоскостей-ограничений вытекает следующее:
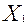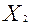- линия пересечения плоскостей-ограничений существует и пересекает координатные плоскости = 0, = 0, 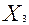= 0 в точках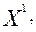 
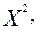
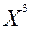соответственно. Ограничения трудоемкости и металлоемкости линейно независимы;
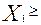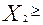- условия 0, 0, 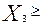0 определяют отрезок линии пересечения, лежащей между координатными плоскостями 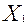= 0, X3 = 0, а конец этого отрезка суть точк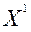и 
и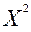 
. Следовательно, оптимальная производственная программа существует (ограничения по трудоемкости и металлоемкости сбалансированы) и реализуется либо в точке 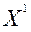, либо в точке X3;
- точка X2 содержит отрицательную вторую компоненту и производственной программой служить не может.
Рис.1. Графическое изображение плоскостей-ограничений в контрольном примере
Находим координаты точки = (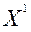
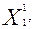
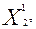
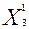) решая систему уравнений:
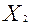0,8 + 0,4 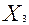= 8800,
0.8 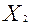+ 2 = 2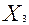8000.
Получаем: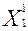 
= 0;
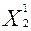= (8800*2 – 0,4*28000)/(0,8*2 – 0,4*0,8) = 5000;
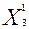= (0,8*28000 – 8800*0,8)/(0,8*2 – 0,4*0,8) = 12000.
Поскольку оба найденных решения неотрицательны и могут определять объемы производства, вычисляем значение целевой функции в точке :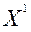
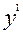= 2400*5000 + 2600*12000 = 43200000.
Находим координаты точки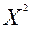 
= (
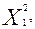
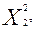
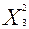), решая систему уравнений:
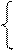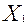0,2 + 0,4 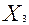= 8800,
5 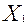+ 2 = 2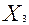8000.
Получаем:
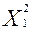= (8800*2 – 0,4*28000)/(0,2*2 – 0,4*5) = -400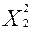0;
= 0;
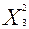= (0,2*28000 – 8800*5)/(0,2*2 – 0,4*5) = 23750.
Значение первой компоненты отрицательное, что ранее было замечено (см. рис. 1). В этом случае значение целевой функции можно вычислить:
2600*23750 – 3000*4000 = 49750000,
но согласно алгоритму решения задачи мы полагаем доход предприятия равным нулю,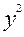 
= 0.
При вычислении координат точки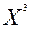 
= (
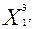
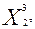
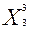) путем решения системы уравнений
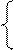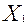0,2 + 0,8 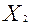= 8800,
5 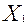+ 0,8 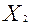= 28000,
получаем:
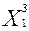= (8800*0,8 – 0,8*28000)/(0,2*0,8 – 0,8*5) = 4000;
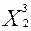= (0,2*28000 – 8800*5)/(0,2*0,8 – 0,8*5) = 1000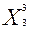0;
= 0.
Поскольку оба найденных решения неотрицательны и могут определять объемы производства, вычисляем значение целевой функции в точке :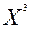
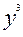= 3000*4000 + 2400*10000 = 36000000.
Расположим полученные значения целевой функции в порядке возрастания:
0 = 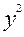< 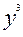= 36000000 < 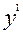= 43200000.
Можно видеть, что оптимальной является первая производственная программа, соответствующая наибольшему значению целевой функции.
Приходим к выводу:
- изделия первого типа не следует включать в оптимальную производственную программу предприятия –
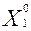= 0;
- объем производства изделий второго типа запланировать в количестве
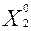= 5000 (шт.);
- объем производства изделий третьего типа запланировать в количестве
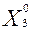= 12000 (шт.).
При этом предприятие получит наибольший возможный доход:
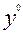= 2400*5000 + 2600*12000 = 43200000 (руб)., т.е. 43.2 млн.руб.
Результаты расчетов представим в виде таблицы 1.
Таблица 1
Оптимальная производственная программа предприятия
| Тип изделия | |||
| Объем производства, шт. | |||
| Доход предприятия, руб. |
