В предыдущих параграфах мы ввели понятия: вектора 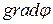 , характеризующего скорость изменения скалярного поля; производную по направлению
, характеризующего скорость изменения скалярного поля; производную по направлению 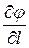 , характеризующую скорость изменения величины
, характеризующую скорость изменения величины 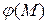 в направлении l; скаляра
в направлении l; скаляра 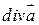 , вектора
, вектора 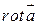 , характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.
, характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.
Пусть 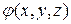 - скалярное поле,
- скалярное поле, 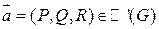 - векторное поле.
- векторное поле.
1) 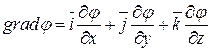
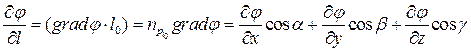
Где 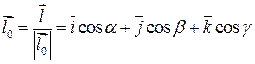 - единичный вектор в направлении
- единичный вектор в направлении 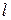 .
.
2) 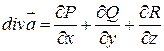 - скаляр.
- скаляр.
3) 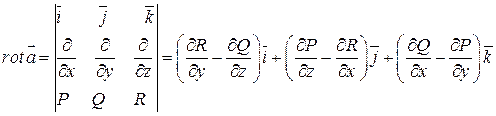 - вихрь вектора
- вихрь вектора 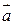 , являющийся вектором.
, являющийся вектором.
Известным английским математиком Гамильтоном было замечено, что все эти (и многие другие) операции можно записать кратко при помощи следующего символического вектора – оператора 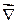 (читается «набла», оператор Гамильтона).
(читается «набла», оператор Гамильтона).
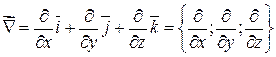
Проекции символического вектора оператора Гамильтона – суть.
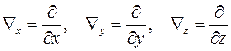 .
.
Сам вектор 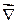 не имеет реального смысла, но результат его применения, как оператора к скалярным или векторным функциям (величинам) дает вполне реальную физическую величину.
не имеет реального смысла, но результат его применения, как оператора к скалярным или векторным функциям (величинам) дает вполне реальную физическую величину.
Тогда символически (обращаясь с 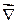 как с вектором в прямоугольной декартовой системе координат и понимая запись
как с вектором в прямоугольной декартовой системе координат и понимая запись 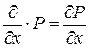 ) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
1) 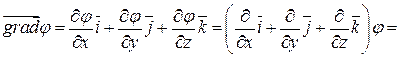
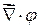
Таким образом, под символическим произведением вектора 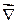 на скаляр
на скаляр 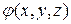 понимается вектор
понимается вектор 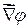 с координатами:
с координатами:
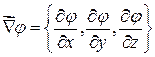
2) 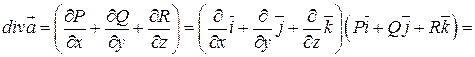
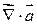
3) Найдем векторное произведение символического вектора:
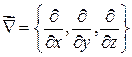 на вектор
на вектор 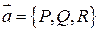 - есть вектор.
- есть вектор.
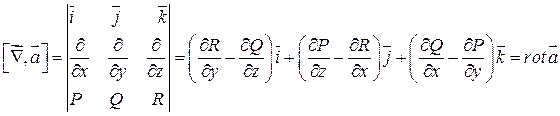

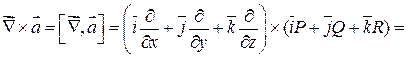
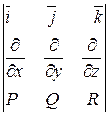 =
=
= 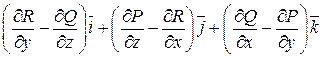 - это вектор, который называют вихрем поля
- это вектор, который называют вихрем поля 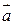 .
. 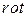 от английского слова
от английского слова  - вращение.
- вращение.
Производную по направлению можно записать в виде:
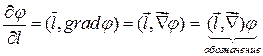 и вообще
и вообще 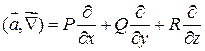 .
.
Таким образом, операции первого порядка могут быть единообразно записаны с помощью символического вектора набла.
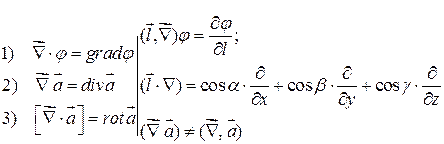
УТВЕРЖДЕНИЕ. Векторные операции I-го порядка линейны относительно своих аргументов.
Доказательство:
Следует из линейности дифференцирования и скалярного и векторных произведений.
НАПРИМЕР.
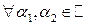 и
и 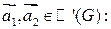
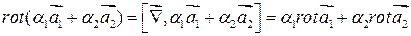
Заметим также, что соотношения, содержащие 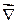 не зависят от выбора системы координат (это доказано для
не зависят от выбора системы координат (это доказано для 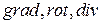 ).
).
Многие формулы векторного анализа легко выводятся при использовании символического вектора 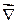 . Нужно понимать, что на функции и векторы, стоящее справа от
. Нужно понимать, что на функции и векторы, стоящее справа от 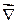 , этот оператор действует как дифференциальный, а функции и векторы, стоящие слева от
, этот оператор действует как дифференциальный, а функции и векторы, стоящие слева от 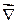 , перемножаются с
, перемножаются с 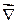 как с обычным вектором по правилам векторной алгебры. В результате такого умножения получается новый дифференциальный оператор.
как с обычным вектором по правилам векторной алгебры. В результате такого умножения получается новый дифференциальный оператор.
Применяя, оператор 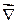 к произведениям векторов и скаляров, будем пользоваться следующим правилом:
к произведениям векторов и скаляров, будем пользоваться следующим правилом:
1. Если оператор 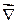 действует на какое-либо произведение, то в первую очередь учитывается его дифференциальный характер, а затем уже векторное свойство.
действует на какое-либо произведение, то в первую очередь учитывается его дифференциальный характер, а затем уже векторное свойство.
2. Чтобы отметить тот факт, что 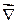 не воздействует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом
не воздействует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом 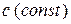 или «стрелкой» (например
или «стрелкой» (например 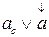 ), который в окончательном результате может быть снят.
), который в окончательном результате может быть снят.
3. Все величины, на которые оператор 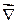 не воздействует, в окончательном результате ставятся впереди
не воздействует, в окончательном результате ставятся впереди 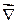 , т.е. слева от него.
, т.е. слева от него.
Так, например, в 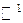 оператор
оператор 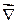 есть оператор дифференцирования
есть оператор дифференцирования
функции одной переменной и тогда правило нахождения производной произведения сводится:
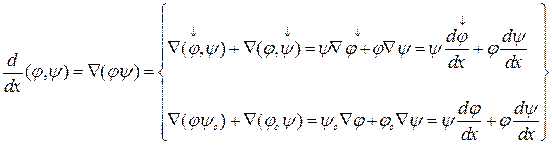
ЗАМЕЧАНИЕ.
Под дифференциальными операциями II-го порядка понимаются операции, в которых символ 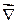 встречается дважды. При этом формулы векторной алгебры считаются справедливыми при замене обычного вектора символическим вектором
встречается дважды. При этом формулы векторной алгебры считаются справедливыми при замене обычного вектора символическим вектором 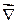 .
.
Усвоим некоторые элементы техники обращения с оператором 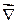 .
.
Вы можете проверить получающиеся формулы в координатах.
1) Пусть 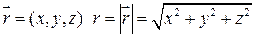 , тогда
, тогда
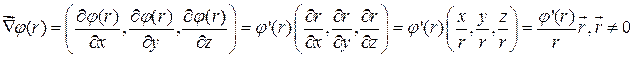
2) 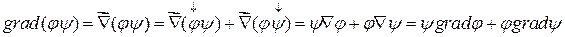
3) 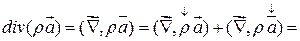
= 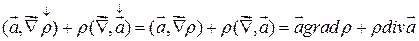
4) 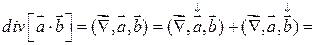
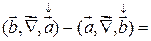
= 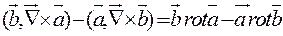
Наряду с обозначениями векторного произведения 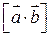 будем использовать и
будем использовать и 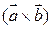 .
.
Нами будет использовано и двойное векторное произведение, известное вам из аналитической геометрии (1 семестр):
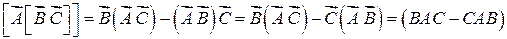
5) 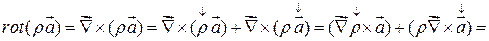
= 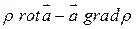 .
.
6) 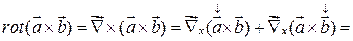
= 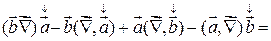
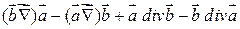 .
.
7) 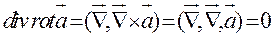 .
.
Вектор 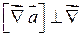 поэтому скалярное произведение равно 0, т.е.
поэтому скалярное произведение равно 0, т.е. 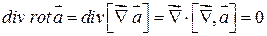 . Т.е. поле вихря вектора
. Т.е. поле вихря вектора 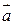 не имеет источников и стоков.
не имеет источников и стоков.
8) 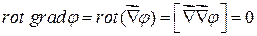 .
.
Т.к. векторы 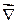 и
и 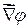 параллельны, т.е. поле вектора
параллельны, т.е. поле вектора 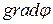 безвихревое.
безвихревое.
9) 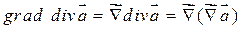 .
.
10) Наряду с 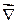 используют оператор Лапласа или Лапласиан.
используют оператор Лапласа или Лапласиан.
Df. Оператором Лапласа или Лапласианом называется закон образования дивергенции от вектора 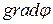 :
:
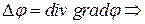 физический смысл. Численное значение Лапласиана определяет плотность источников (если
физический смысл. Численное значение Лапласиана определяет плотность источников (если 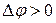 ) или стоков (если
) или стоков (если 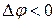 ) векторного поля
) векторного поля 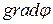 .
.
Справедлива формула:
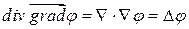 , где символ
, где символ 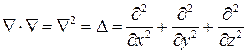 , так что
, так что 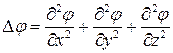 .
.
Df. Скалярное поле 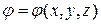 , удовлетворяющее условию
, удовлетворяющее условию 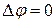 , называется лапласовым или гармоническим полем.
, называется лапласовым или гармоническим полем.
Дифференциальные операции II-го порядка можно для наглядности записать в виде таблицы:
Скалярное поле 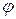 | Векторное поле 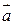 | ||
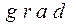 | 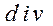 | 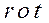 | |
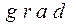 | ---------------------------- | 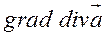 | ---------------------------------- |
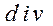 | 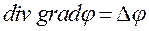 | ----------------- | 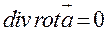 |
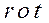 | 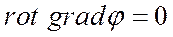 | ----------------- | 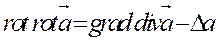 |
ТАБЛИЦА ОСНОВНЫХ ВЕЛИЧИН ПОЛЯ
| Наименование величины и обозначение | Определение или запись с помощью операторов Гамильтона и Лапласа | Формула записи в декартовых координатах |
| -1- | -2- | -3- |
Градиент скалярного поля 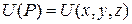 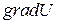 | 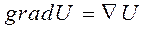 | 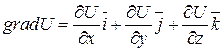 |
Расходимость векторного поля 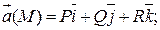 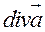 ; ; | 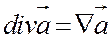 | 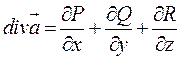 |
Поток векторного поля 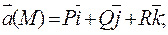 П П | 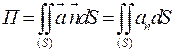 ; в частности через замкнутую поверхность S: ; в частности через замкнутую поверхность S: 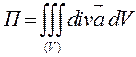 (Теорема Остроградского) (Теорема Остроградского) | 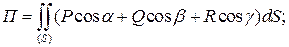 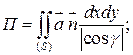 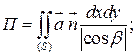 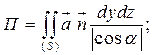 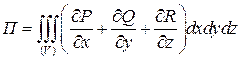 |
Ротор векторного поля 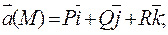 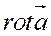 ; ; | 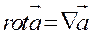 | 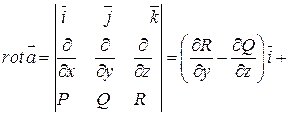 + + 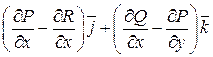 |
| -1- | -2- | -3- |
Работа (линейный интеграл) векторного поля вдоль контура 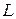 ; W ; W | 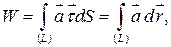 где где 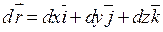 | 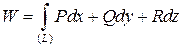 . . 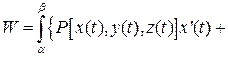 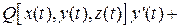 + + 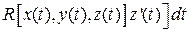 |
Циркуляция векторного поля 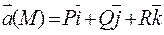 вдоль контура l. Ц вдоль контура l. Ц | 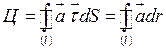 . . | 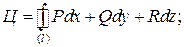 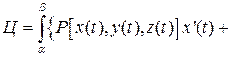 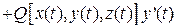 + + + + 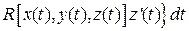 . . |
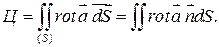 | 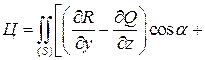 + + 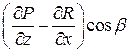 + + 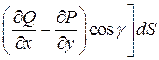 . . |
 2015-04-17
2015-04-17 1208
1208







