Df.1 Пусть 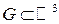 ,
, 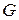 - область, векторное поле
- область, векторное поле 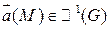 . Ротором (вихрем) векторного поля
. Ротором (вихрем) векторного поля 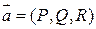 называется:
называется:
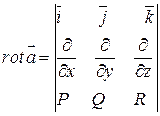 (1)
(1)
(1) операторная форма записи 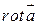 . Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
. Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
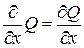 и т.д. Тогда:
и т.д. Тогда:
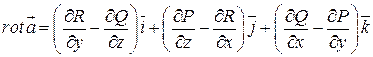
Очевидно, операция 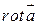 ставит в соответствие векторному полю
ставит в соответствие векторному полю 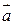 векторное поле
векторное поле 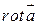 , определенное в G.
, определенное в G.
Th.1 (ТЕОРЕМА СТОКСА)
Пусть 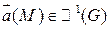 , G – область.
, G – область. 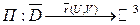 - кусочно-гладкая;
- кусочно-гладкая; 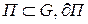 - кусочно-замкнутый контур, ограничивающий П. Тогда:
- кусочно-замкнутый контур, ограничивающий П. Тогда:
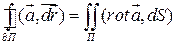 (3)
(3)
(3) – формула Стокса.
(Б/д).




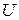
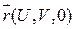
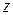
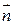
 |  | ||

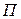
 | |||
 | |||




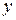
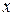
При этом сторона поверхности и направление обхода контура 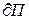 согласованы. Как правило, обычно выбирается внешняя сторона П.
согласованы. Как правило, обычно выбирается внешняя сторона П.
Th.2 (ТЕОРЕМА ГРИНА)
Пусть 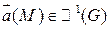 ,
, 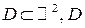 - область,
- область, 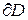 - кусочно-гладкая граница D, ориентированная против часовой стрелки;
- кусочно-гладкая граница D, ориентированная против часовой стрелки; 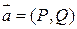 , тогда:
, тогда:
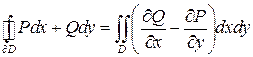 (4)
(4)
(4) – формула Грина.
(Б/д).
Покажем, что (4) – есть частный случай формулы Стокса. Причем это нельзя считать доказательством, т.к. при доказательстве (3) используется (4).
Итак: плоскость П зададим так: 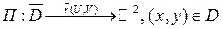 .
.
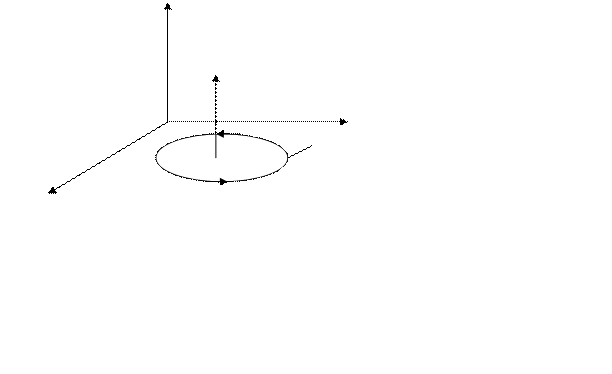
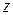
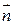
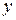
D 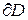
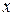
Тогда 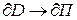 , кроме того
, кроме того 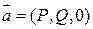 .
.
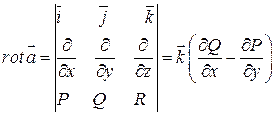
Из (3) 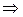
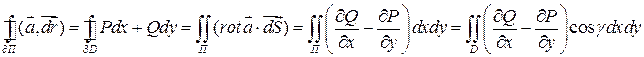 (по теореме о сведении поверхностного интеграла II-го рода к двойному)
(по теореме о сведении поверхностного интеграла II-го рода к двойному)
Здесь 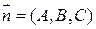 , очевидно
, очевидно 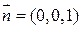 , т.е. С=1. Итак:
, т.е. С=1. Итак:
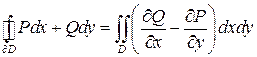
СЛЕДСТВИЕ ИЗ Th.1
Пусть 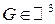 , G -область,
, G -область, 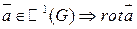 определен в G и инвариантен относительно системы координат.
определен в G и инвариантен относительно системы координат.
 Доказательство:
Доказательство:


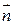

 Г
Г
D ● 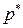 G
G
 ●
● 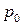
Рассмотрим 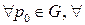 направление, задаваемое
направление, задаваемое 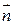 . П – плоскость, перпендикулярная
. П – плоскость, перпендикулярная 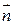 , проходящая через точку
, проходящая через точку 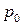 .
.
Пусть D – поверхность: 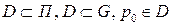 .
.
Г – граница (кусочно-гладкая) поверхности D. Направление обхода D согласовано с 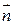 . Применим формулу Стокса для поверхности D с нормалью
. Применим формулу Стокса для поверхности D с нормалью 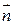 и границей Г:
и границей Г:
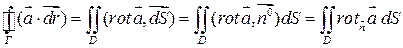
где 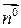 =
= 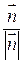 ,
, 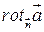 - проекция
- проекция 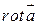 на направление
на направление 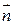 . По теореме о среднем для поверхностного интеграла I-го рода:
. По теореме о среднем для поверхностного интеграла I-го рода:
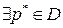 , что
, что
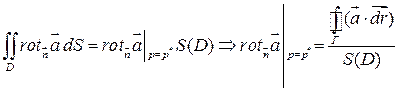 (*)
(*)
Отметим, что 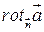
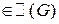 - непрерывное векторное поле.
- непрерывное векторное поле.
Перейдем в (*) к пределу при 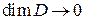 (
(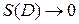 ,
, 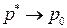 ). В силу непрерывности
). В силу непрерывности 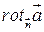 найдем:
найдем:
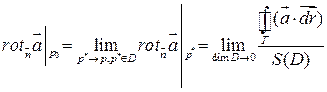
Т.к. 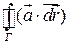 и
и 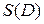 не зависят от выбора системы координат, то
не зависят от выбора системы координат, то 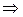
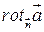 не зависит от выбора системы координат
не зависит от выбора системы координат 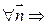
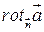 инвариантен относительно выбора системы координат. (Достаточно взять три неколлинеарных вектора
инвариантен относительно выбора системы координат. (Достаточно взять три неколлинеарных вектора 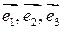 и считать, что
и считать, что 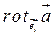 , проекции
, проекции 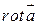 на
на 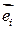 . Есть его координаты).
. Есть его координаты).
СЛЕДСТВИЕ 2.
Пусть 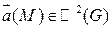 (т.е.
(т.е. 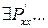 и они непрерывны в G)
и они непрерывны в G) 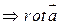 определяет соленоидальное поле в G, т.е.
определяет соленоидальное поле в G, т.е. 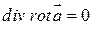 .
.
САМОСТОЯТЕЛЬНО.
Действительно 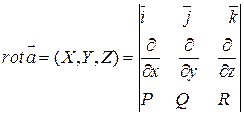 .
.
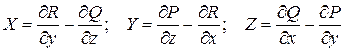 :
: 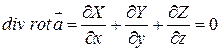
 2015-04-17
2015-04-17 533
533








