Пусть векторное поле 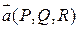 непрерывно в G;
непрерывно в G; 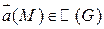 /
/
Df.1 Выражение 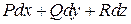 (1) называется полным дифференциалом в G, если
(1) называется полным дифференциалом в G, если 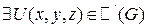 , что:
, что:
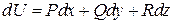 (2)
(2)
т.к. 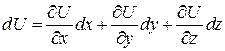 , то (1) – полный дифференциал
, то (1) – полный дифференциал 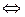 если
если 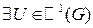 и
и
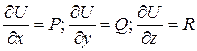 (3)
(3)
Напомним, что для 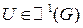 :
:
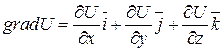 (4)
(4)
тогда очевидна следующая Лемма:
(1) – полный дифференциал 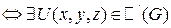 и
и 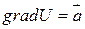 .
.
Доказательство следует из (3) и (4).
Имеют место следующие утверждения:
1) 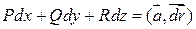 полный дифференциал в G.
полный дифференциал в G.
2) 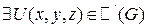 , что
, что 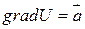 .
.
3) 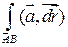 не зависит от формы пути,
не зависит от формы пути, 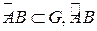 - кусочно-гладкая.
- кусочно-гладкая.
4) 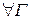 - замкнутого кусочно-гладкого,
- замкнутого кусочно-гладкого, 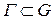 :
:
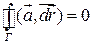
Df.2 G - область. Обозначим D – область в G, 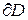 - граница области (замкнутый простой контур в
- граница области (замкнутый простой контур в 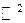 или поверхность в
или поверхность в 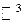 ). Тогда G – односвязная
). Тогда G – односвязная 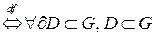 .
.
 Односвязное
Односвязное




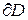 G D
G D
G
Неодносвязное
Th.1 Пусть векторное поле 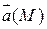 определено в односвязной области G,
определено в односвязной области G, 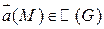 , тогда условия (1), (2), (3) и (4) равносильны.
, тогда условия (1), (2), (3) и (4) равносильны.
Доказательство:
Для доказательства введем два вспомогательных утверждения:
(3’) 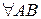 - ломанной,
- ломанной, 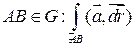 не зависит от формы пути.
не зависит от формы пути.
(4’) 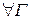 - замкнутой простой ломанной,
- замкнутой простой ломанной, 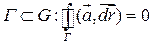 .
.
Доказательство проведем по следующей схеме:
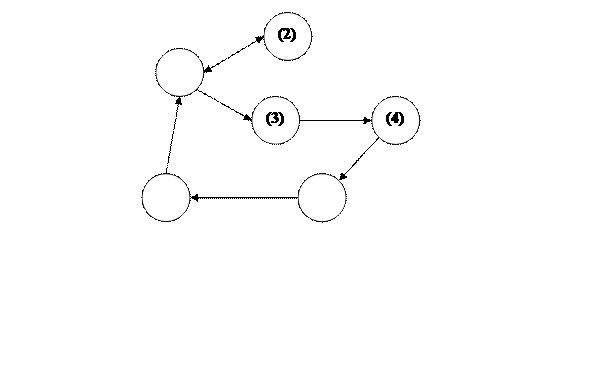
(1)
(3’) (4’)
Отсюда будет следовать, что все условия эквивалентны.
Отметим, что (1) 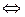 (2) доказано Леммой. Далее ограничимся рассмотрением плоского случая, т.е.
(2) доказано Леммой. Далее ограничимся рассмотрением плоского случая, т.е. 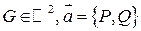 .
.
а) (1) 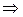 (3)
(3)
Дано: 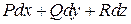 - полный дифференциал, т.е.
- полный дифференциал, т.е. 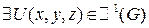 , что
, что 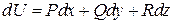 .
.

 ●
● 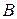
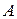 ●
●
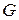
Пусть 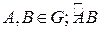 - гладкая кривая.
- гладкая кривая. 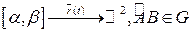 .
.
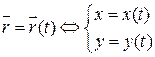
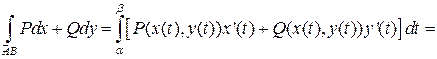 =
= 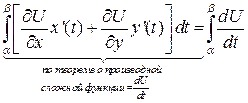 =
= 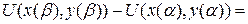
= 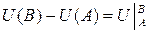 .
.
Пусть теперь 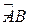 - кусочно-гладкая:
- кусочно-гладкая:

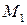
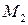
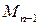
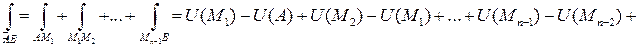
+ 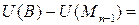
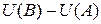 .
.
Таким образом, также дается формула вычисления 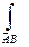 , если подынтегральное выражение полный дифференциал.
, если подынтегральное выражение полный дифференциал.
б) (3) 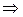 (4)
(4)
Пусть 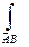
 не зависят от формы пути. Рассмотрим любой контур Г – замкнутый кусочно-гладкий,
не зависят от формы пути. Рассмотрим любой контур Г – замкнутый кусочно-гладкий, 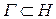 .
.



 ●
●
 ● ●
● ● 
 ●
●
По свойству кратного интеграла II-го рода 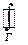 не зависит от начальной точки.
не зависит от начальной точки. 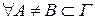 , тогда:
, тогда: 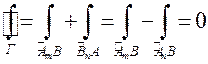 .
.
в) (4) 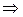 (4’)
(4’)
Это очевидно, т.к. замкнутая ломанная – частный случай кусочно-гладкой кривой.
г) (4’) 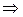 (3’)
(3’)
Ограничимся случаем непересекающихся ломанных.
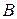
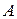
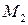
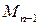
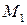
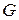
Дано: 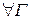 - замкнутой ломанной
- замкнутой ломанной 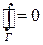 .
.
Доказать: 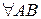 - ломанной, соединяющей A и B
- ломанной, соединяющей A и B 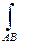 не зависит от формы пути.
не зависит от формы пути.
Пусть 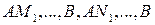 - две произвольные ломанные, тогда:
- две произвольные ломанные, тогда:
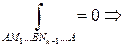 разобьем:
разобьем: 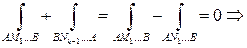
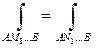 .
.
Можно доказать, что все останется в силе, если ломанные пересекаются.
д) (3’) 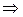 (1)
(1)
Дано: 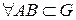 - ломанной,
- ломанной, 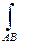 не зависит от формы пути.
не зависит от формы пути.
Доказать: что 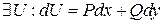
Доказательство существования проведем построением.
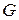
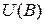
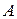 ● ●
● ● 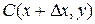
0 x
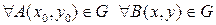 , т.к. G открыто, то
, т.к. G открыто, то 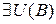 , что
, что
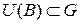 . Возьмем
. Возьмем  . Определим
. Определим 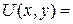
= 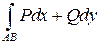 . Это можно сделать, т.к. интеграл не зависит от формы пути и при фиксированной точке А зависит только от конечной точки В(x,y).
. Это можно сделать, т.к. интеграл не зависит от формы пути и при фиксированной точке А зависит только от конечной точки В(x,y).
Найдем:
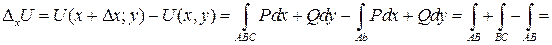
= 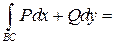
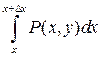 .
.
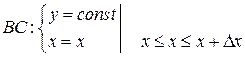
Т.к. Р(x,y) непрерывная в G следовательно по теореме о среднем:
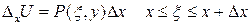 , причем при
, причем при 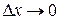 ,
, 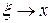
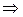
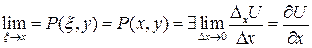 .
.
Аналогично показывается, что 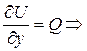 полный дифференциал.
полный дифференциал.
СЛЕДСТВИЕ.
Доказательство теоремы позволяет установить метод отыскания U(x,y,z).
Пусть 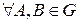 .
.
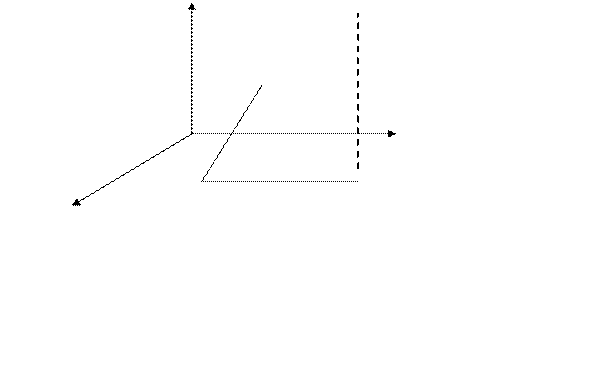
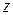 ●
● 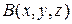
● 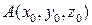
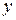
● ●
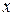
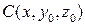
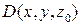
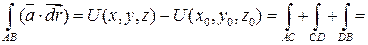
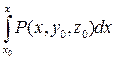 +
+
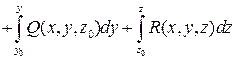 .
.
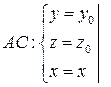
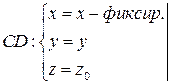
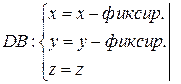
Df.3 Векторное поле 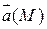 , определенное в G, называется потенциальным, если оно удовлетворяет любому из равносильных условий (1), (2), (3) и (4); U называют потенциалом (потенциальной функцией) поля
, определенное в G, называется потенциальным, если оно удовлетворяет любому из равносильных условий (1), (2), (3) и (4); U называют потенциалом (потенциальной функцией) поля 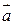 .
.
Очевидно, что U(M) определяется с точностью до константы.
Th.2 Пусть 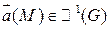 , G – односвязная область. Тогда
, G – односвязная область. Тогда 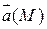 потенциально в G
потенциально в G 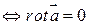 .
.
Доказательство:
Необходимость.
Пусть 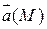 потенциально в G.
потенциально в G. 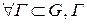 - замкнутая кусочно-гладкая граница:
- замкнутая кусочно-гладкая граница: 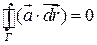 .
.
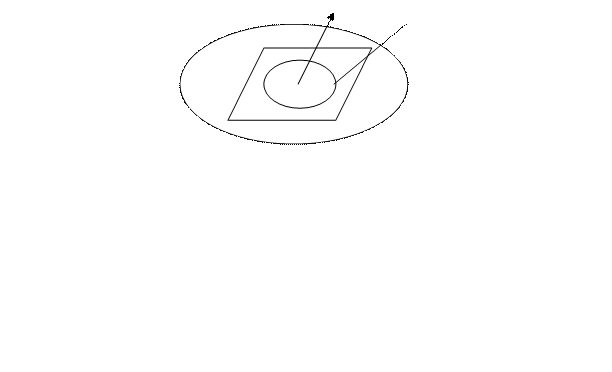
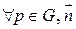 - произвольный нормальный вектор из точки
- произвольный нормальный вектор из точки 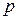 к плоскости, содержащей кривую Г.
к плоскости, содержащей кривую Г.
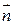
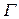
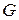
 ●
● 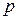
По инвариантному определению 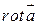 :
:
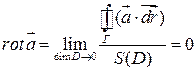
Т.к. 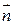 произвольного направления, то пусть
произвольного направления, то пусть 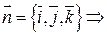
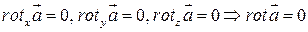 .
.
Достаточность.
Пусть 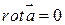 .
. 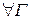 - замкнутой
- замкнутой 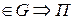 - поверхность, что
- поверхность, что 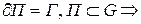 (по теореме Стокса)
(по теореме Стокса) 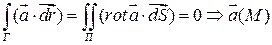 - потенциально.
- потенциально.
Df.4 Пусть векторное поле 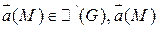 называется бизвихревым в G
называется бизвихревым в G 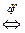 если
если 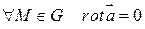 .
.
Тогда теорему 2 можно переформулировать (перефразировать) следующим образом:
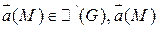 - потенциальное
- потенциальное 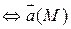 безвихревое.
безвихревое.
Таким образом, отсутствие вихрей является и необходимым и достаточным условием потенциальности поля.
Следует отметить, что необходимым и достаточным условием потенциальности поля является также равенство нулю циркуляции поля по любому замкнутому контуру.
Следует иметь ввиду, что приведенные выше рассуждения справедливы только в случае, когда поле 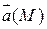 определено во всех внутренних точках контура Г. Если же хотя бы в одной внутренней точке некоторого замкнутого контура поле
определено во всех внутренних точках контура Г. Если же хотя бы в одной внутренней точке некоторого замкнутого контура поле 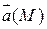 не определено, то циркуляция по этому контуру может и не обращаться в нуль, хотя поле и потенциально.
не определено, то циркуляция по этому контуру может и не обращаться в нуль, хотя поле и потенциально.
Рассмотрим еще одно векторное поле – так называемое соленоидальное, или трубчатое поле.
Df.5 Поле вектора 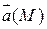 называется соленоидальным или трубчатым, если в каждой точке поля
называется соленоидальным или трубчатым, если в каждой точке поля 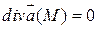 .
.
Или имея в виду физический смысл 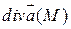 , можно сказать, что соленоидальное поле – это такое поле, в котором нет источников и стоков.
, можно сказать, что соленоидальное поле – это такое поле, в котором нет источников и стоков.
Примером соленоидального поля является поле вихря вектора 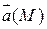 .
.
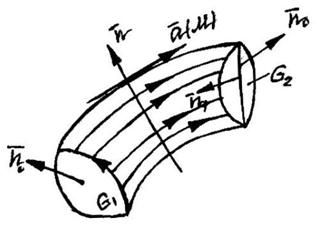
Основное свойство соленоидального поля состоит в том, что в нем векторные линии не могут нигде ни начинаться, ни кончаться, они могут уходить в бесконечность или быть замкнутыми.
ПРИМЕР.
Проверить на потенциальность поле: 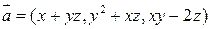 . Найти потенциал и вычислить
. Найти потенциал и вычислить 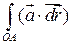 , где
, где 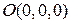 и
и 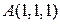 .
.
Решение:
Очевидно, 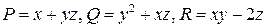 - имеют производные любого порядка в
- имеют производные любого порядка в 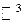 , т.е.
, т.е. 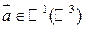 .
.
а) Проверка потенциальности:
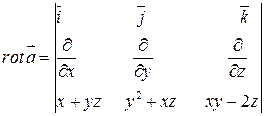 =
= 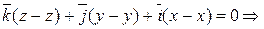 поле потенциально.
поле потенциально.
б) Определяем потенциал:
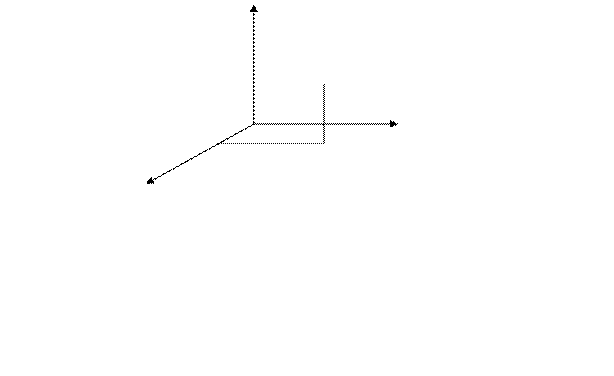 1 способ.
1 способ.
z
● 
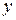
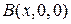 ● ●
● ● 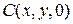
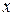
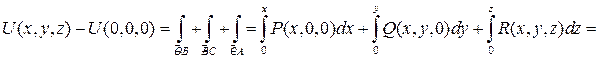 =
= 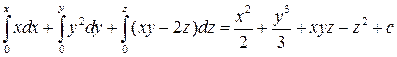 , где
, где 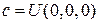 .
.
2 способ.
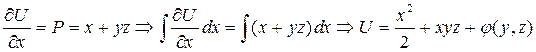 ;
;
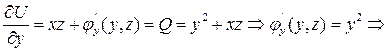
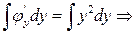
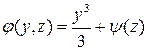 ;
;
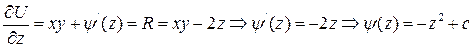 ;
;
Итак:
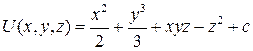 .
.
в) 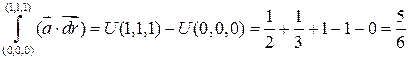 .
.
 2015-04-17
2015-04-17 456
456








