Математические методы и модели искусственного интеллекта: нечеткая логика, генетические алгоритмы, нейронные сети и др. Интеллектуальный анализ данных. Управление знаниями

В основе нечеткой логики лежит теория нечетких множеств, изложенная в серии работ Л. Заде в 1965-1973 годах. Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Л. Заде, формулируя это главное свойство нечетких множеств, базировался на трудах предшественников. В начале 1920-х годов польский математик Лукашевич трудился над принципами многозначной математической логики, в которой значениями предикатов могли быть не только «истина» или «ложь». В 1937 году еще один американский ученый М. Блэк впервые применил многозначную логику Лукашевича к спискам как множествам объектов и назвал такие множества неопределенными.

Нечеткая логика как научное направление развивалась непросто, не избежала она и обвинений в лженаучности. Даже в 1989 году, когда примеры успешного применения нечеткой логики в обороне, промышленности и бизнесе исчислялись десятками, Национальное научное общество США обсуждало вопрос об исключении материалов по нечетким множествам из институтских учебников.

Первый период развития нечетких систем (конец 60-х – начало 70-х гг.) характеризуется развитием теоретического аппарата нечетких множеств. В 1970 году Беллман совместно с Заде разработали теорию принятия решений в нечетких условиях.

В 70-80 годы (второй период) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). И. Мамдани в 1975 году спроектировал первый функционирующий на основе алгебры Заде контроллер, управляющий паровой турбиной. Одновременно стало уделяться внимание вопросам создания экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений нашли широкое применение в медицине и экономике.

Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других. Кроме того, немалую роль в развитии нечеткой логики сыграло доказательство знаменитой теоремы FAT (Fuzzy Approximation Theorem) Б. Коско, в которой утверждалось, что любую математическую систему можно аппроксимировать системой на основе нечеткой логики.

Информационные системы, базирующиеся на нечетких множествах и нечеткой логике, называют нечеткими системами.

Достоинства нечетких систем:

· функционирование в условиях неопределенности;

· оперирование качественными и количественными данными;

· использование экспертных знаний в управлении;

· построение моделей приближенных рассуждений человека;

· устойчивость при действии на систему всевозможных возмущений.

Недостатками нечетких систем являются:

· отсутствие стандартной методики конструирования нечетких систем;

· невозможность математического анализа нечетких систем существующими методами;

· применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений.

Теория нечетких множеств. Главное отличие теории нечетких множеств от классической теории четких множеств состоит в том, что если для четких множеств результатом вычисления характеристической функции могут быть только два значения – 0 или 1, то для нечетких множеств это количество бесконечно, но ограничено диапазоном от нуля до единицы.

Нечеткое множество. Пусть U – так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в данном классе задач, например множество всех целых чисел, множество всех гладких функций и т.д. Характеристическая функция множества 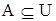– это функция 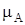, значения которой указывают, является ли 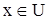элементом множества A:

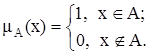
В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение 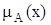– степенью принадлежности элемента x нечеткому множеству A.

Более строго: нечетким множеством A называется совокупность пар

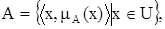
где 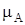– функция принадлежности, то есть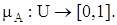

Пусть, например, U ={a, b, c, d, e}, 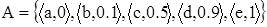. Тогда элемент a не принадлежит множеству A, элемент b принадлежит ему в малой степени, элемент c более или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом множества A.

Пример. Пусть универсум U есть множество действительных чисел. Нечеткое множество A, обозначающее множество чисел, близких к 10, можно задать следующей функцией принадлежности (рис. 21.1):

,

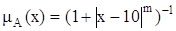где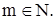

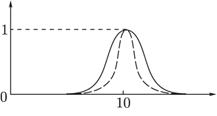
Рис. 21.1. Функция принадлежности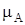

Показатель степени m выбирается в зависимости от степени близости к 10. Например, для описания множества чисел, очень близких к 10, можно положить m = 4, для множества чисел, не очень далеких от 10, m = 1.

Носителем нечеткого множества A называется четкое множество 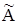таких точек в U, для которых величина 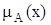положительна, то есть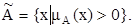

Ядром нечеткого множества A называется четкое множество 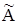таких точек в U, для которых величина 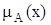= 1.

Множеством уровня 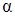( 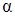-срезом) нечеткого множества A называется четкое подмножество универсального множества U, определяемое по формул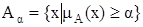е , где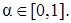

Функцию принадлежности называют нормальной, если ядро нечеткого множества содержит хотя бы один элемент.

Операции над нечеткими множествами. Для нечетких множеств, как и для обычных, определены основные операции: объединение, пересечение и инверсия/дополнение.

Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:

Максиминные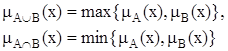
Алгебраические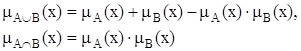
Ограниченные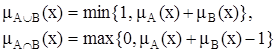

Дополнение нечеткого множества во всех трех случаях определяется одинаково:

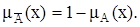
При максиминном и алгебраическом определении операций не будут выполняться законы противоречия и исключения третьего:

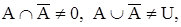
а в случае ограниченных операций не будут выполняться свойства идемпотентности и дистрибутивности:

,

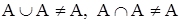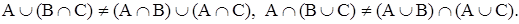
Можно показать, что при любом построении операций объединения и пересечения в теории нечетких множеств приходится отбрасывать либо законы противоречия и исключения третьего, либо законы идемпотентности и дистрибутивности.

Нечеткая логика. Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.

Нечеткая переменная характеризуется тройкой <b, X, A>, где b – наименование переменной, X – универсальное множество (область определения b), A – нечеткое множество на X, описывающее ограничения (то есть b A(x)) на значения нечеткой переменной a.

Лингвистической переменной называется набор <b, T, X, G, M>, где b – наименование лингвистической переменной, Т – множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X (множество T называется базовым терм-множеством лингвистической переменной), G – синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности генерировать новые термы (значения), М – семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, то есть сформировать соответствующее нечеткое множество.

Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная «возраст» может принимать следующие значения: «очень молодой», «молодой», «среднего возраста», «старый», «очень старый» и др. Ясно, что переменная «возраст» будет обычной переменной, если ее значения – точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.

Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению «молодой» может соответствовать функция принадлежности, изображенная на рисунке 21.2.

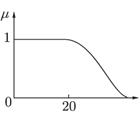
Рис. 21.2. Функция принадлежности значения «молодой» лингвистической переменной «возраст»

Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме «если…, то…» и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:

существует хотя бы одно правило для каждого лингвистического терма выходной переменной;

для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечетких правил. Для реализации логического вывода необходимо выполнить следующее:

· Сопоставить факты с каждым из правил и определить степень соответствия, назначив текущую силой правил;

· Для каждого правила, сила которого больше заданного порога, вычислить достоверность левой части;

· Для каждого правила с помощью оператора импликации вычислить достоверность правой части;

· Для многих результатов, полученных по различным правилам, выбрать одно (усредненное).

Нейронные сети (НС) – очень мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости, нелинейные по свой природе. Как правило, нейронная сеть используется тогда, когда неизвестны предположения о виде связей между входами и выходами (хотя, конечно, от пользователя требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты).

На вход нейронной сети подаются представительные данные и запускается алгоритм обучения, который автоматически анализирует структуру данных и генерирует зависимость между входом и выходом. Для обучения НС применяются алгоритмы двух типов: управляемое («обучение с учителем») и неуправляемое («без учителя»).

Простейшая сеть имеет структуру многослойного персептрона с прямой передачей сигнала (рис. 21.3), которая характеризуется наиболее устойчивым поведением. Входной слой служит для ввода значений исходных переменных, затем последовательно отрабатывают нейроны промежуточных и выходного слоев. Каждый из скрытых и выходных нейронов, как правило, соединен со всеми элементами предыдущего слоя (для большинства вариантов сети полная система связей является предпочтительной). В узлах сети активный нейрон вычисляет свое значение активации, беря взвешенную сумму выходов элементов предыдущего слоя и вычитая из нее пороговое значение. Затем значение активации преобразуется с помощью функции активации (или передаточной функции), и в результате получается выход нейрона. После того, как вся сеть отработает, выходные значения элементов последнего слоя принимаются за выход всей сети в целом.

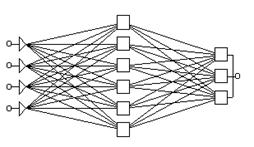
Рис. 21.3. Пример нейронной сети – трехслойного персептрона с прямым распространением информации

Наряду с моделью многослойного персептрона, позднее возникли и другие модели нейронных сетей, различающихся по строению отдельных нейронов, по топологии связей между ними и по алгоритмам обучения. Среди наиболее известных сейчас вариантов можно назвать НС с обратным распространением ошибки, основанные на радиальных базисных функциях, обобщенно-регрессионные сети, НС Хопфилда и Хэмминга, самоорганизующиеся карты Кохонена, стохастические нейронные сети и т.д. Существуют работы по рекуррентным сетям (т.е. содержащим обратные связи, ведущие назад от более дальних к более ближним нейронам), которые могут иметь очень сложную динамику поведения. Начинают эффективно использоваться самоорганизующиеся (растущие или эволюционирующие) нейронные сети, которые во многих случаях оказываются более предпочтительными, чем традиционные полносвязные НС.

Для моделей, построенных по мотивам человеческого мозга, характерны, как легкое распараллеливание алгоритмов и связанная с этим высокая производительность, так и не слишком большая выразительность представленных результатов, не способствующая извлечению новых знаний о моделируемой среде. Попытаться в явном виде представить результаты нейросетевого моделирования – довольно неблагодарная задача. Поэтому основной удел этих моделей, являющихся своеобразной "вещью в себе", – прогнозирование.

Важным условием применения НС, как и любых статистических методов, является объективно существующая связь между известными входными значениями и неизвестным откликом. Эта связь может носить случайный характер, искажена шумом, но она должна существовать. Известный афоризм “ garbage in, garbage out ” (“ мусор на входе – мусор на выходе ”) нигде не справедлив в такой степени, как при использовании методов нейросетевого моделирования. Это объясняется, во-первых, тем, чтоитерационные алгоритмы направленного перебора комбинаций параметров нейросети оказываются весьма эффективными и очень быстрыми лишь при хорошем качестве исходных данных. Однако, если это условие не соблюдается, число итераций быстро растет и вычислительная сложность оказывается сопоставимой с экспоненциальной сложностью алгоритмов полного перебора возможных состояний. Во-вторых, сеть склонна обучаться прежде всего тому, чему проще всего обучиться, а, в условиях сильной неопределенности и зашумленности признаков, это – прежде всего артефакты и явления "ложной корреляции".

Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса. Впоследствии, после разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.

Генетические алгоритмы. «Отцом» генетических алгоритмов по праву считается Д. Холланд, метод вначале назывался репродуктивным планом Холланда. В дальнейшем генетические алгоритмы развивались в работах учеников Холланда: Д. Голдберга и К. Де Йонга – именно в них и закрепилось название метода.

Генетические алгоритмы – это раздел эволюционного моделирования, заимствующий методические приемы из теоретических положений генетики.

Генетические алгоритмы – адаптивные методы поиска, которые используются для решения задач функциональной оптимизации. Представляют собой своего рода модели машинного исследования поискового пространства, построенные на эволюционной метафоре. Характерные особенности: использование строк фиксированной длины для представления генетической информации, работа с популяцией строк, использование генетических операторов для формирования будущих поколений.

Генетические алгоритмы применяются для решения следующих задач:

· оптимизация функций;

· разнообразные задачи на графах (задача коммивояжера и т.д.);

· настройка и обучение искусственной нейронной сети;

· задачи компоновки;

· составление расписаний;

· игровые стратегии;

· аппроксимация функций;

· искусственная жизнь;

· биоинформатика.

Преимущества генетических алгоритмов: универсальность, высокая обзорность поиска, нет ограничений на целевую функцию, любой способ задания функции.

Недостатки генетических алгоритмов: относительно высокая вычислительная стоимость и квазиоптимальность.

Когда надо использовать генетический алгоритм: много параметров, плохая целевая функция, комбинаторные задачи.

Когда не надо использовать генетический алгоритм: задача хорошо решается традиционными методами, требуется высокая точность решения.