Метод неопределенных множителей Лагранжа

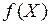Пусть и 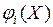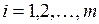непрерывно дифференцируемы в окрестности точки 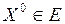и ранг матрицы Якоби 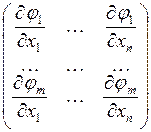в этой точке равен .

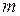Функцию 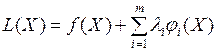называют функцией Лагранжа. Коэффициенты 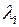– неопределенные множители Лагранжа.

Необходимые условия существования условного экстремума.

Для того, чтобы точка 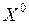являлась точкой условного экстремума функции 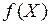при связях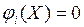 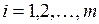необходимо, чтобы её координаты при некоторых значениях 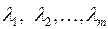удовлетворяли системе уравнений

,

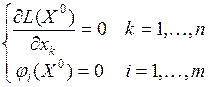т.е. 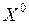– стационарная точка функции Лагранжа и её координаты удовлетворяют уравнениям связи.