Hаибольшим значением функции 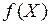 в области
в области 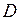 называется число
называется число 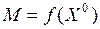 , если
, если 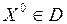 и для всех точек
и для всех точек 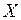 этой области выполняется неравенство
этой области выполняется неравенство 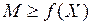 .
.
Наименьшим значением функции 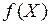 в области
в области 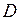 называется число
называется число 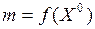 , если
, если 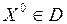 и для всех точек
и для всех точек 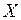 этой области выполняется неравенство
этой области выполняется неравенство 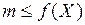 .
.
Теорема Вейерштрасса. Для функции, непрерывной на ограниченном замкнутом множестве, существует на этом множестве точка, в которой функция принимает наибольшее значение и точка, в которой функция принимает наименьшее значение.
Функция, дифференцируемая в ограниченной области и непрерывная на её границе, достигает своего наибольшего и наименьшего значений либо в стационарных точках, либо в граничных точках области.
Пример 4. Определить наибольшее и наименьшее значения функции 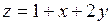 в области D:
в области D: 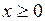 ,
, 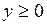 ,
, 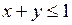 .
.
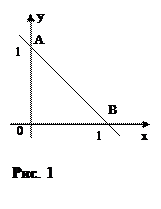 Решение. Указанная область есть треугольник (рис. 1). Стационарных точек функция не имеет, так как
Решение. Указанная область есть треугольник (рис. 1). Стационарных точек функция не имеет, так как 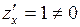 ,
, 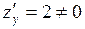 .
.
Исследуем функцию на границах области. Граница состоит из трех отрезков [ ОА ], [ АВ ], [ ОВ ]. На отрезке 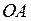
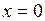 , значит, для точек этого отрезка
, значит, для точек этого отрезка 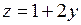 ,
, 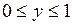 .
.
Таким образом, задача свелась к нахождению наименьшего и наибольшего значений функции 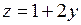 на отрезке
на отрезке 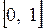 . Так как
. Так как 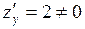 , то функция принимает эти значения на концах отрезка, т. е. в точках
, то функция принимает эти значения на концах отрезка, т. е. в точках 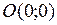 и
и 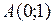 . Находим
. Находим 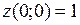 ,
, 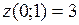 .
.
Аналогично, для отрезка 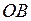
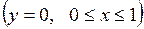 задача сводится к отысканию наибольшего и наименьшего значений функции
задача сводится к отысканию наибольшего и наименьшего значений функции 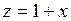 на отрезке
на отрезке 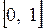 . Они реализуются на концах отрезка, т. е. в точках
. Они реализуются на концах отрезка, т. е. в точках 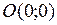 и
и 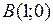 , так как
, так как 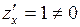 . Находим
. Находим 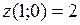 .
.
Отрезок 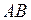 определяется уравнением
определяется уравнением 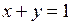 или
или 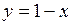 при
при 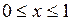 . Для этого отрезка имеем
. Для этого отрезка имеем 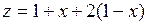 или
или 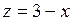 и
и 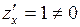 , т. е. наибольшее и наименьшее значения функция принимает на концах отрезка
, т. е. наибольшее и наименьшее значения функция принимает на концах отрезка 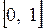 , в точках
, в точках 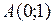 и
и 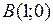 . Сравнивая все полученные значения, заключаем, что
. Сравнивая все полученные значения, заключаем, что
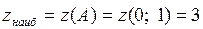 ,
, 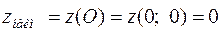 .
.
Пример 5. Положительное число 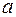 требуется разбить на три неотрицательных слагаемых так, чтобы их произведение было наибольшим.
требуется разбить на три неотрицательных слагаемых так, чтобы их произведение было наибольшим.
Решение. Обозначим слагаемые 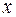 ,
, 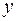 и
и 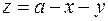 . Ищем максимум функции
. Ищем максимум функции 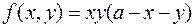 . По смыслу задачи функция рассматривается внутри замкнутого треугольника
. По смыслу задачи функция рассматривается внутри замкнутого треугольника 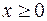 ,
, 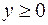 ,
, 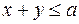 .
.
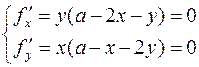 . Внутренняя стационарная точка
. Внутренняя стационарная точка 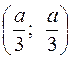 .
.
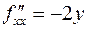 ,
, 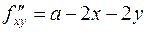 ,
, 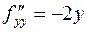 .
.
Матрица Гессе в стационарной точке 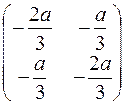 . Так как
. Так как 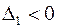 , а
, а 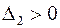 , то в точке
, то в точке 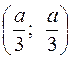 функция достигает максимума
функция достигает максимума 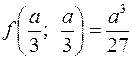 .
.
Поскольку на контуре треугольника 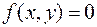 , то этот максимум будет наибольшим значением.
, то этот максимум будет наибольшим значением.
Пример 6. (КИМ ЕГЭ 2006) Три числа, принадлежащих соответственно отрезкам 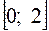 ,
, 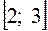 и
и 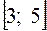 , являются первыми членами арифметической прогрессии. Найдите, какие значения может принимать величина
, являются первыми членами арифметической прогрессии. Найдите, какие значения может принимать величина 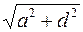 , где
, где 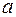 – первый член, а
– первый член, а 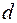 – разность прогрессии.
– разность прогрессии.
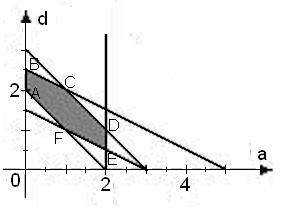 Решение. Из условия задачи имеем:
Решение. Из условия задачи имеем: 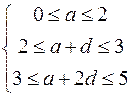 . Рассмотрим функцию
. Рассмотрим функцию 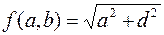 , определенную на шестиугольнике
, определенную на шестиугольнике 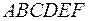 .
. 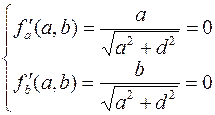 , Стационарная точка
, Стационарная точка 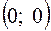 не принадлежит шестиугольнику
не принадлежит шестиугольнику 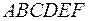 .
.
Найдем координаты вершин шестиугольника: 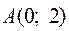 ,
, 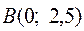 ,
, 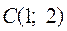 ,
, 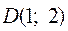 ,
, 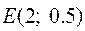 ,
, 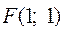 . Вычислим значения функции в вершинах:
. Вычислим значения функции в вершинах: 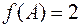 ,
, 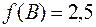 ,
, 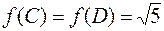 ,
, 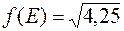 ,
, 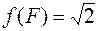 .
.
Значит, функция может принимать значения из отрезка 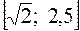 .
.
 2015-04-17
2015-04-17 803
803







