1.Типы плоских волн. Распространение возмущений в неограниченной среде.
Уравнения движения упругой среды в перемещениях можно записать в виде.
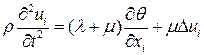
где 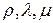 – соответственно плотность среды и параметры Ламе.
– соответственно плотность среды и параметры Ламе.
Вводя следующие безразмерные параметры
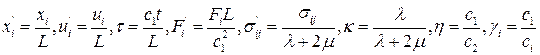
где 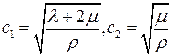 – скорости распространения упругих волн.
– скорости распространения упругих волн.
Тогда уравнения равновесия можно записать в следующем виде
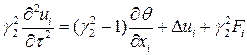
При этом штрихи в безразмерных параметрах будем опускать
Рассмотрим выписанные уравнения для случая, когда все величины зависят только от одной координаты, для определенности пусть будет 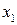 . Тогда уравнения равновесия распадаются на три независимых уравнения
. Тогда уравнения равновесия распадаются на три независимых уравнения
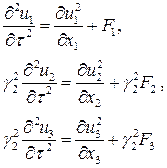
Как видим, каждое уравнение представляет собой уравнение колебаний струны. Решением такого уравнения при отсутствии массовых сил является суперпозиция прямой и обратной волн
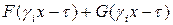
Первое из описанных уравнений описывает так называемые продольные волны, а второе поперечные.
Распространение возмущений в бесконечной упругой среде. Как видно из уравнений для случая, когда все величины зависят от одной координаты, поперечные и продольные волны распространяются независимо. Поэтому для их изучения рассмотри следующую задачу.
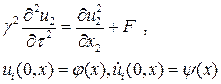
Применим к этому уравнению поочередно преобразования Фурье и Лапласа тогда получаем
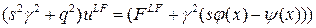
Теперь, если рассмотреть вспомогательную задачу:
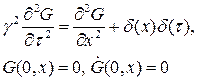
Тогда легко увидеть, что
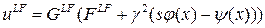
Тогда можем последовательно записать
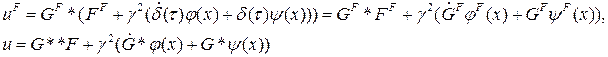
Таким образом, для решения исходной задачи необходимо решить вспомогательную задачу.
Имеем
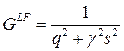
Тогда (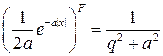 )
)
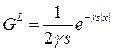
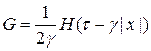
Тогда
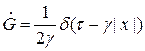
Тогда имеем,
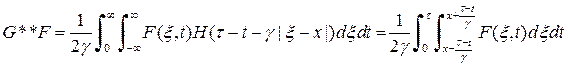
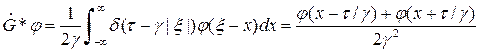
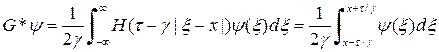
И, таким образом, получаем
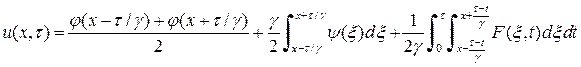
Задания.
Найти НДС упругой среды при
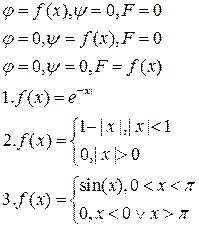
 2015-04-17
2015-04-17 290
290







