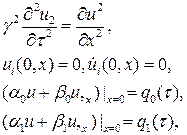
Решение данной задачи может быть представлено в виде
Применяя преобразование Лапласа, получим
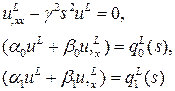
Общее решение уравнения имеет вид
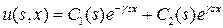
Подставляя данное решение, в систему граничных условий, получаем следующую систему линейных алгебраических уравнений:
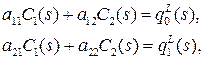
где
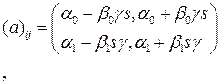
Решая данную систему, находим
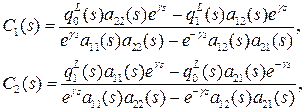
Таким образом, преобразованное по Лапласу решение будет выглядеть следующим образом:
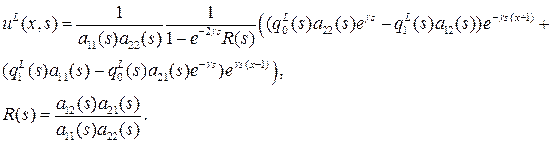
Так как 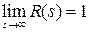 , то существует такое
, то существует такое 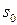 , что при
, что при 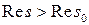 выполняется неравенство
выполняется неравенство 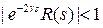 , а потому множитель перед скобкой раскладывается в равномерно сходящийся в этой плоскости ряд:
, а потому множитель перед скобкой раскладывается в равномерно сходящийся в этой плоскости ряд:
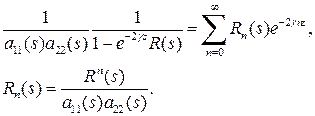
Тогда выражение для перемещения может быть записано в виде
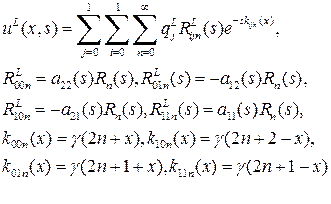
Оригиналы каждого из членов ряда находятся с помощью свойств преобразования Лапласа. И мы получаем
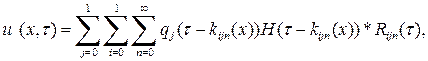
Для конечного момента времени мы получаем ограниченное число элементов ряда, т.е.
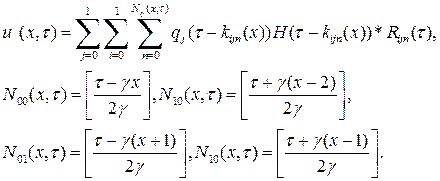
Переписывая выражение для свертки через интеграл, получим
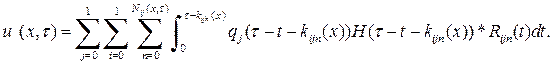
Задания. Рассчитать напряженно-деформированное состояние слоя при
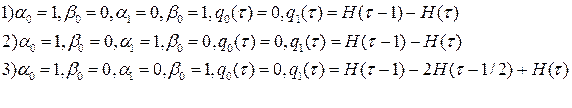
 2015-04-17
2015-04-17 199
199







