При нахождении области определения функции удобно использовать теоретический материал таблицы 1.
Таблица 1.
| № | Вид функции | Пример функции | Наличие ограничений у данного вида функции |
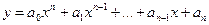 , где , где 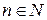 . .
| 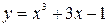
| У данной функции нет ограничений, т.е.  D (y) =R. D (y) =R.
| |
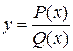 , где P (x) и Q (x) - многочлены от х. , где P (x) и Q (x) - многочлены от х.
| 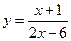
| Ограничение: Q(x) 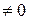 . .
| |
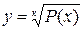 , к - четное число, P(x)- многочлен от х. , к - четное число, P(x)- многочлен от х.
| 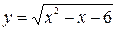
| Ограничение: 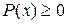 . .
| |
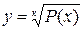 , к - нечетное число, P(x)- многочлен от х. , к - нечетное число, P(x)- многочлен от х.
| 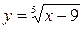
| У данной функции нет ограничений, т.е.  D(y)=R. D(y)=R.
| |
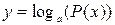 , а>0, , а>0, 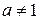 , P(x)- многочлен от х. , P(x)- многочлен от х.
| 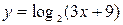
| Ограничение: 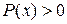 . .
| |
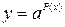 , а>0, , а>0, 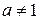 , P(x)- многочлен от х. , P(x)- многочлен от х.
| 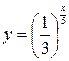
| У данной функции нет ограничений, т.е.  D(y)=R. D(y)=R.
| |
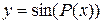 , , 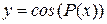 , P(x)- многочлен от х. , P(x)- многочлен от х.
| 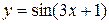
| У данной функции нет ограничений, т.е.  D(y)=R. D(y)=R.
| |
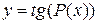 , P(x)- многочлен от х. , P(x)- многочлен от х.
| 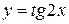
| Ограничение: 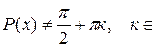 Z. Z.
| |
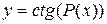 ,
P(x)- многочлен от х. ,
P(x)- многочлен от х.
| 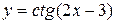
| Ограничение: 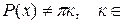 Z. Z.
| |
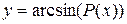 , , 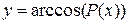 ,
P(x)- многочлен от х. ,
P(x)- многочлен от х.
| 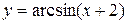
| Ограничение: 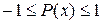 . .
| |
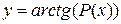 , , 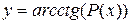 ,
P(x)- многочлен от х. ,
P(x)- многочлен от х.
| 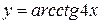
| У данной функции нет ограничений, т.е.  D(y)=R. D(y)=R.
|
 2015-04-01
2015-04-01 506
506








